|
第100話
数理論理の話 〜第 100話記念特大号〜
|

「本稿の目的」
今回は、第100話記念号として、入門までを体系的に書いてみようという試みです。前回に引き続き、予想を立てて、それを確認するという方向で展開します。ただし、将来への布石として、外れの予想も行いました。また、最後の方では、自然数の上で、不等号を完全には特徴付けられないということにも触れました。何でもかんでもやればできるというものでもなく、手に負えないもののあることを認識しましょう。
本 文 目 次
1.はじめに
2.命題論理
3.演繹定理
4.述語論理
5.充足定理
6.コンパクト性定理
7.おわりに
著者 坂田 明治
第100話 数理論理の話 〜第 100話記念特大号〜
1.はじめに
理科好き子供の広場も、ついに100話を達成しました。
ということで、第100話記念特大号になります。今回は数理論理の話ですが、いつものように、あまり予備知識を必要としません。普通に、数理論理の入門となる内容なので、「激ムズでいーから。」という意見(第99話)に副(そ)えないかもね。でも、気にしないもんね。
また、途中で飽きたため、かなりいい加減なところもあります。毎度のことですが、頭から正しいと信じたりせず、自分でよく考えて判断しましょう。
最初に注意を一つ。程度の悪い教師にありがちな問題行動を述べておきます。


式(2)を式(1)へ代入しましょう。

式(3)のような回答を書く生徒がいます。すると、程度の悪い教師は、正解を式(4)として、式(3)を間違いだと。

何も説明しないか、せいぜい説明しても、( )の中を先に計算するとか何とか。この説明で間違っている訳ではないけれども、式(3)のように書いてしまった理由が考えられていません。正解が書けさえすればいいのか。
今度は、式(2)の代入先として式(5)を考えてみましょう。

代入すると、式(6)のようになり、y をただ置き換えただけで何の問題もありませんね。

更に、式(7)を代入元として、式(1)、式(5)へ代入してみましょう。



この場合、式(8)、式(9)は、y をただ置き換えただけで何の問題もありません。いや、ここまで来ると、むしろ、式(4)の( )はどこから出てきたのかが問題となります。つまり、そのまま文字を書き換えてうまく行く場合と、それではうまく行かず、どこから出てきたのかが解らない( )を付けなくてはならない場合があり、この違いは何かということです。
代入するというのは、代入前に、代入元の式が計算されており、その結果を代入するということです。そして、式(6)、式(8)、式(9)が正しいのは、それぞれ、順に、加法結合法則、乗法結合法則、乗算は加算に優先という計算順序の約束事があるからです。そう考えると、代入時に( )が付いており、それが、何らかの法則や約束事によって省略されていると解釈できますね。
こう考えてくると、最初から式に、計算の順序が付いていれば問題ないはずです。元々
( )は計算の優先順位を付けるものでした。これは、( )の中が外より先という優先順位です。であれば式にキチンと( )を付けて優先順位を表すなら置き換えただけでうまく行くはずです。
式(1)と式(2)を( )付きで書き直すと、


となります。式(11)を式(10)へ代入するに際して、ただ単に文字を書き直すだけで、
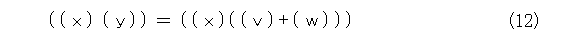
が出てきます。ついでに、式(5)も書き直して、

式(13)に式(11)を代入して、
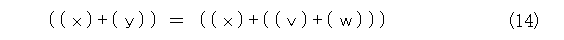
となり、 ただ単に文字を書き直すだけで正しい式が出てきます。
これで、形式的に文字を書き直すだけで正しい式を出すことができました。つまり、式を形式的な文字の書き直しだけで正しく代入が行われた形にすることはできます。
しかしながら、( )がやたら出てくると見難くてうっとーしくなります。その上、項が増えると、色々な( )のつけ方が出てきて式まで増え(カッコが干渉するため、多数の式を用意しなければならない)、益々、見難くて、面倒でうっとーしくなります。これが、誤解が生じない限り(一通りに解釈でき、しかも見やすくなるように)、カッコを省略するとの意味です。
「カッコ付けるとカッコ悪くなる。」という教訓ですね。
2.命題論理
この章では命題論理を公理的に取り扱います。等号は出てきません。その代わりが同値記号です。毎度のことだけど、記号や文字が文字化けしたりして、書きにくいったらありゃしない。そこで、式を書くときは記号を使って画像で作り、文章中では文字で書くことにします。
まずは、論理記号を導入しましょう。
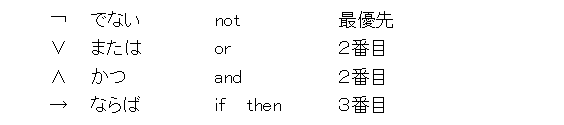
一応、日本語と英語の読み方と、作用する順序を書いておきました。順序を決めておくと、( )の省略ができて式が見やすくなります。なお、「でない」を「否定」と呼ぶことも多々あります(どっちを使うかは書いてるときの気分による)。
例えば、
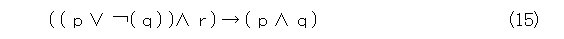
で優先順位に従って( )を省略すると、

となって見やすくなります。
なお、論理記号を日本語で読むと、つい、日本語の読み方による意味にとらわれてしまい、変な解釈になってしまうため、英語で読んだ方がいいかも。英語なら意味が解らないから。あっ、それは俺だけか。
少し試してみましょう。元の命題とその対偶は同値というのがあります。

対偶といえば、対偶を取るとおかしな意味になるという現象、俗にいう対偶漫談です。早速、やってみましょう。
「しからないと、宿題しない」という命題は、「しからない、ならば、宿題しない」と書けますね。この対偶をとると、「宿題をする、ならば、しかる」となって、「宿題をすると、しかる」となります。何だよ、これ。宿題なんかやる気にならないじゃないか。
いくらでも、作れます。途中を省略して書くと、「落第しないと、勉強しない」の対偶は、「勉強すると、落第する」だし、「税務署が取り立てにこないと、税金を払わない」の対偶は、「税金を払うと、税務署が取り立てにくる」となります。なんか、もう、勉強したり、税金を払いたくなくなりましたね。
「風吹けば、桶屋が儲かる」の対偶は、「桶屋が儲からないなら、風が吹かない」です。桶屋の儲けが地球現象に関わってくるとは。
以上のように、対偶をとって、変な意味になるのを喜ぶことを対偶漫談といいます。いくらでも作れる上に、よい思考訓練にもなります。ということで、10個以上作るのが読者の宿題。
よく、こんなことになった原因は、日本語がいい加減だからだとか、論理が、日本語を扱えるほど精密ではないとかいう人がいます。要するに、日本語では対偶が成り立たないといいたいのでしょう。しかし、この説明は正しくありません。
そもそも、式(17)は形式的なもの、あるいは、形式化したものです。対偶漫談は、その形式化されたところで、言葉の意味を考え、意味と形式がごちゃまぜになり、そしておかしな意味に解釈されるにより生じます。
意味を考えるのあれば、式の意味(言葉の意味ではない)を考えて、その式の意味で解釈できるように読まなければいけませんね。考え直してみましょう。「 p ならば q 」という論理式は、原因とか仮定(p のこと)から、結果とか結論(q のこと)が出てくることを意味します。そうすると、対偶は、結果が否定されたら原因が否定されることを意味します。したがって、式(17)は、原因から結論が出てくるということと、結論が否定されたら原因が否定されるということとが同値を意味します。こう書くと、この論法はよく使う論法であると解りますね。
ここまで考えると、対偶の読み方が明らかになります。つまり、結論の否定から、仮定の否定が出てくるように読みます。そういうようにして、ここで挙げた例を読み直してみましょう。
「しからないと、宿題しない」の対偶は、「宿題をしているから、しかったんだろ」と読めます。このの場合、「宿題をしているから、しかられたんだろ」は誤りです。主語が省略されているので、元の命題から読み取って、それに合わせる必要があります。普通、しかるのは親で、宿題をしているのは子供でしょう。それを念頭において読みます。以下、同じです。
「落第しないと、勉強しない」の対偶は、「勉強しているのは、落第したからだ」(もう落第したくないよう)と読めます。
「税務署が取り立てにこないと、税金を払わない」の対偶は、「税金を払ったのは、税務署が取り立てたからだろ」と読めます。
「風吹けば、桶屋が儲かる」の対偶は、「桶屋が儲からないのは、風が吹かないからだ」と読めます。
いずれにしても、おかしな意味にはならないですね。読者は10個以上作った例を読み直して確かめましょうね。
これから、公理的にやるので関係ありませんが(本当か?)、一応、真偽表について触れておきます。命題論理で、最初に出てくるのは真偽表です。以下のような表です。最近はプログラミング教育を、小学生のときからやるとか何とかのため、真偽表もよく知られているようです。
ここでは、0 を真、1 を偽としています。しかし、記号は何でもよいので、自分の使いやすい記号で真偽表を書き直しましょう。
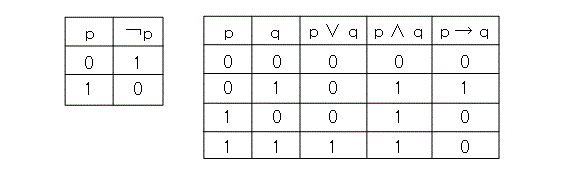
まあ、論理式があれば、簡単に真偽表が作れるので、論理式を10個位作って、その真偽表を書くのは読者の宿題です。
ところで、論理式の真偽が、常に真だけになるものをトートロジーとか恒真命題と呼び、常に偽だけになるものを恒偽命題と呼びます。トートロジーになっている論理式を10個位挙げるのは、読者の宿題です。
さて、真偽表があると色々解ります。例えば、真偽が同じ論理式は同値です。これを利用して、論理記号を、基本的なものと、略記として取り扱われるものとに分けることができます。以下の真偽表を書いて同値を確かめるのは読者の宿題です。

これから、「でない」と「または」を基本的なものとして、その他は略記としてよいですね。公理的にやる際も、ここに示した、「でない」と「または」を基本的なものとして、その他は略記とします。
やっと本論に入れます(なんで、前置きがこんなに長くなったんだ)。まず、論理記号は用意しました。次に、無限に多くの命題変数を用意します。これは、p 、 q 、 r 、・・・ です。この上で、論理式を、

と帰納的に定義します。
次は、公理です。公理は、それなりの体系ができるものであれば、なんでもよいのだけど、ここでは、天下り的に以下の公理を採用します。

それにしても、「り」が付くかどうかで印象が全く逆になる言葉ですね。「俺は天下を目指すぞ。」といえば、「おおー、よくいった。がんばってくれ。」となるのに、「俺は天下りをするぞ。」というと、・・・
今度は、推論規則です。推論規則は、以下の「置換」と「三段論法」です。

最後は証明です。証明を、次の条件を満たす論理式の有限列であるとします。

そして、証明の最後の論理式は、証明によって「証明される」と呼びます。とまあ、こうなんだけど、論理式を並べただけだと解りにくいので、説明文の挿入を許すことにします。もちろん、説明文は読む人が解るようにするためだけなので、形式的な処理や、機械的な処理をするときは無視されます。
ところで、公理(4)を見ていると、どうしても、「 r 」を「 r でない」に置換したくなってきます。置換すれば、式(18)の証明ができますね。

さらに、p を論理式Q、q を論理式R、r を論理式Pに置換すると、
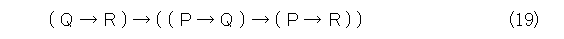
となります。式(19)はよく使う論理式です。以下のように読むと解りやすいでしょう。
「 QならばRのとき、PならばQが成り立てば、PならばRが成り立つ」
さらに、図式化すれば、なお、いっそう解りやすくなります。
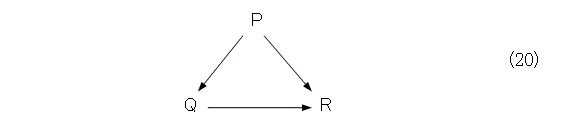
図式(20)を眺めると、PならばQと、QならばRとから、PならばRが出てくると予想されるでしょう(予想を立てるのはよいことです)。三段論法によって確かめましょう。QならばRと証明された式(19)に対して、三段論法を適用すると、

が出ます。更に、PならばQと式(21)に 三段論法を適用して、

が出ます。
このことを、式(23)のように書いて、「PならばQと、QならばRとから、PならばRが出る」とか、「PならばQと、QならばRとから、PならばRが導かれる」と読みます。
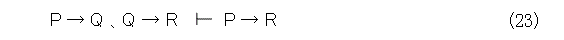
もっと一般的に、論理式Qが、論理式P1 、P2 、・・・、Pn (この中に不要なものがあっても構わない)から導かれるということを、式(24)のように書きます。
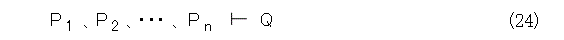
特に、Qが公理だけから導かれることを式(25)のように書きます。

平たくいえば、式(24)で導入した記号の、左辺が原因とか仮定で、右辺が結果とか結論です(なんか、どっかで同じ話があったような)。式(25)は、公理だけから導かれるということで、つまり、何も仮定しなくても出てくるということですね。
また、

の両方が証明可能であるとき、論理式PとQは同値であると呼び、

と書きます。
少し、練習しましょう。
まずは、簡単なところから。公理(3)に置換を使えば、ただちに式(28)が出ます。

次に、二重否定が元と同値になることを証明してみましょう。なお、式(24)で導入した記号を一々付けると、見難くてうっとうしいので、重要なところにだけ付けることにします。
公理(2)から、

公理(1)から、

式(23)を使って、

が成り立つ。
ここで、
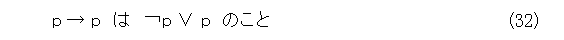
だから、p のところを「 p でない」に置換して、

式(28)を使って、

これは、

のこと。更に、p のところを「 p でない」に置換して、

公理(4)で、p のところを「 p でない」、r のところを p 、q のところを「 p でない でない でない」に置換して、
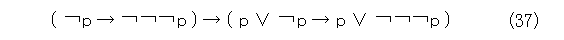
式(36)と式(37)に三段論法を適用して、

式(32)に式(28)を適用して、

式(39)と式(38)に三段論法を適用して、

式(28)を適用して、

書き直して、

式(35)と式(42)とから、

が証明できた。
これで、公理と推論規則の使い方が解ってきたと思います。ということで、交換、結合、分配、ド・モルガンの法則、が同値という意味で成り立つことと、元の論理式と対偶が同値であることの証明は読者の宿題です。
3.演繹定理
第2章で公理化した体系を、公理系Lということにしましょう。こんな大層なことを書いても、第99話を読まれた人から、「公理化したって、また、お釈迦様の掌から出られないのじゃないか。」と吹っかけられそうですね。どうでしょうか。
それでは、出られるか出られないかの予想を立ててみましょう。お釈迦様の掌に相当するものが何かを決めなくてはなりませんね。なんでしょうか。
これがもし、第95話で出てきたインケンゼミで、「パシリ君」と「う」だったら、「う」が「パシリ君」の顔色を伺って、「話の流れからいって、真偽表ですよね。」というはずです。「う」は「パシリ君」が、「公理化するのに、わざわざ真偽表なんて出すのは何か目的がある筈だ。」と確実に見抜くでしょう。よく顔色見ていますから。しかし、実際は、こうならないでしょう。むしろ、余計な話はせず、公理と推論規則だけ書いて、「こんなもの誰がやっても同じ。色々な論理式の証明はできて当然だ。お釈迦様の掌問題からやれ。」となる公算大です。「う」は真っ青になって、どんないい訳をするのでしょうか。
もっとも、こんなとき、「パシリ君」は、「そんなことじゃ、お釈迦様どころか、俺の掌からも出られんぞ。こういうときは、産まれてから現時点に至るまでの知識を使って考えろ。」と貴重な助言をしますが。
ちなみに、第93話に出てきた秋葉原行軍隊の場合は、いきなり損氏少佐が、「悪童子大尉は、命題論理の完全性をやること。くぐつ大尉は、演繹定理をやること。できるまで秋葉原行軍許可は出さんぞ。」と天下り的に押し付けることでしょう。
それはともかく、通常、かなり早い時期から、真偽と論理記号の関係を学ばれることでしょう。その後、逆、裏、対偶とか、所によってはブール代数の話になるところもあります。こう考えて、お釈迦様の掌の第1選択は、真偽表でしょうか。予想が外れたら、また、考え直せばいいので、結果をあまり気にする必要はありません。それでは、もっと細かく詰めて行きましょう。
論理式は、論理記号から帰納的に定義しました。当然ですが、一般の論理式の真偽は不明です。また、公理系Lで証明ができる論理式かどうかも不明です。そこで範囲を狭める必要があります。
最初から読み直すと、わざわざ公理化して、推論規則を導入し、証明を定義したという流れは、証明できる論理式を扱うためですね。真偽表の方で考えてみると、正しい論理式は、真偽値が常に真である論理式、すなわち、トートロジーであるとみなせます。証明できることと正しいということは大体同じと考えて、「トートロジーと証明できることとは同じなのではないか。」と予想しましょう。
後は、この予想が当たっているか、外れているかを検証することです。
まず、公理がトートロジーであることは真偽表を書けば確かめられます。当然、確かめるのは読者の宿題です。次に、トートロジーから、置換によって推論される論理式がトートロジーであることは自明です(真偽表書いて確かめるのは読者の宿題)。最後に、Pがトートロジーで、PならばQがトートロジーのとき、Qがトートロジーになるのも明らかだから(真偽表書いて確かめるのは読者の宿題)、三段論法によって推論される論理式もトートロジーです。
これで証明できる論理式はトートロジーであるということが解りました。
なんだこりゃ。わざわざ公理化しても、トートロジーの範囲内にあるだけじゃないのか。いままでの苦労はなんだったんだ。と思う人も多いかと。まあまあ、これで完結する訳ではないので、考察を続けましょう。
証明可能な論理式はトートロジーの範囲内にあることから、全ての論理式が証明できる訳ではないことが解ります。何でもよいから、トートロジーにならない論理式を持ってくれば証明できません。沢山ありますので、10個位例を挙げるのは読者の宿題です。
また、論理式Pが証明可能(トートロジー)であれば、「Pでない」は証明可能にはならない(トートロジーにならない)ことが解ります。つまり、Pと「Pでない」は同時に証明可能にはならないということです。このようなことを「無矛盾」とか「整合的」とかいいます。つまり、公理系Lは無矛盾なんですね。なお、この「無矛盾」は命題論理だけの概念ではありません。述語論理など幅広く使われています。
それから、無矛盾は、Pかつ「Pでない」(この論理式を「矛盾」ともいう)が証明可能にならないことや、全ての論理式が証明可能という訳ではないことなどと同値になります。もちろん、同値の証明は読者の宿題です。
さて、予想の残り半分を確かめましょう。つまり、「トートロジーな論理式は証明可能」であるかを考えましょう。これが成り立つと、トートロジーと証明可能とは同じになります。
論理式をそのままの形で扱うと面倒なので、標準形にしてから扱います。以下が、標準形です。
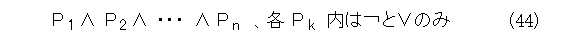
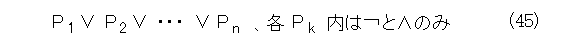
式(44)を and 標準形とか、かつ標準形とか、論理積標準形とか、連言標準形と呼び、式(45)を or 標準形とか、または標準形とか、論理和標準形とか、選言標準形と呼びます。
公理系Lでは、交換、結合、分配、ド・モルガンの法則が同値という意味で成り立つことと、二重否定が元と同値であることから、どんな論理式も標準形に変形でき、しかも、証明可能な論理式を標準形に変形した論理式も証明可能になります。簡単に確かめられるので、読者の宿題です。
一方で、真偽表の方では、どんな論理式も、真偽値が全く同じ標準形が存在します。当然、トートロジーと真偽値が全く同じ標準形が存在します。ちなみに、真偽表では、真偽値が全く同じときに同値といい、やっぱり、交換、結合、分配、ド・モルガンの法則、二重否定などが元と同値になります。これを確かめるのは読者の宿題です。
ここで、真偽表を元にして標準形を作る方法を考えましょう。真偽表(46)で、「これ」と書いてある論理式の「または標準形」を求めます。
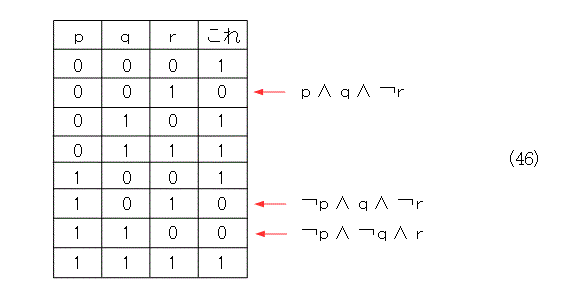
まず、真偽値が真である( 0 が真で、1 が偽)行を選び、各命題変数の真偽値から「でない」と「かつ」を使って、このときに真となる論理式を作ります。こうして作った論理式を「または」で結びます。
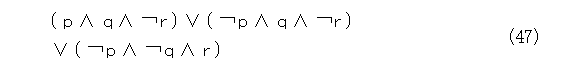
このようにして、真偽表から「または標準形」が作れます。当然、「かつ標準形」の作り方については読者の宿題です。
以上から、標準形についてのみ考えればよくなりました。で、標準形が二つあり、どちらを使うかですが、「かつ」の方が、性質を内側に押し込められて使いやすそうです。
つまり、PかつQがトートロジーであれば、当然、PとQはトートロジーになります。そして、P、Qが共に証明可能であれば、PかつQも証明可能です。これらを確かめるのは読者の宿題です。
では、式(44)がトートロジーとします。このとき、各Pk はトートロジーとなります。逆に、各Pk が証明可能であれば、式(44)は証明可能になります。すると、次は、Pk について考えればいい訳ですね。
とはいっても、この先、どうすればいいのか解りません。
こんなときは、簡単な例を考えましょう。どう考えても、一番簡単なトートロジーは式(32)です(「 p でない」、または「 p 」の方)。この論理式をよく眺めましょう。命題変数とその「でない」が含まれています。確かに、真偽表を書けば、命題変数と、その「でない」が含まれていなければトートロジーにならないことが解ります。
これから、Pk は式(48)のような形をしていることが解ります。

式(48)の「 p でない」、または「 p 」は、式(31)にある通り証明可能です。しかも、公理(2)と三段論法によって、式(48)、すなわち、元になったPk が証明可能です。
これで、トートロジーな論理式が証明可能であると解りました。結局、証明可能とトートロジーは全く同じで、お釈迦様の掌から全然出られなかったことになります。
ちなみに、このことから、公理系Lは真偽表に関して完全であるといいます。だって、全く同じなんだから。
しかし、これじゃ、わざわざ公理化しても価値が認められませんよね。なんとかしなくては。
とはいっても手詰まりです。こんなときは、どっかの国の大企業がよくやる手を使ってみましよう。どんな手かというと、「まず使わない、しょうもない機能を追加し、差別化と称してその機能を売りにして発売する。」というものです。
さあ、そこで、これを真似してみましょう。つまり、証明可能でない論理式(当然、トートロジーではない)を公理に付け加えれば、体系が拡大されて、お釈迦様の掌から出られると予想されます。
じゃあ、「 p でない」を公理に追加しましょう。当然、これはトートロジーではありませんから、体系が広がるはずです。なんか、わくわくしますね。
まず、二重否定が元に戻ることを知ってるから、置換によって、p を「 p でない」に置き換えましょう。すると、「 p でない でない」となります。従って、p が証明できたわけです。ということは、Pと「P でない」は同時に証明可能ということになり、矛盾した体系になります(無矛盾ではない)。
かくして、予想は外れ、失意のどん底に落ちてしまいました。このやり方のどこが悪かったのでしょうか。もう一度どっかの国の大企業の戦略を見てみると、「まず使わない」という部分を使っていないことが解ります。真似の仕方に問題があったのかも知れません。
矛盾が出てくるところを、もう一度、よく読み返してみると、置換が直接の原因になっていると解ります。そうだとすると、置換を使用禁止にすればいいのではないかと予想されます。つまり、付け加える論理式に対し、その論理式中に出てくる命題変数の置換を一切禁止にすればよいのではないかと。(そういえば、前に住んでいた所の近くに、「チカン禁止」と書いた看板が電柱に 巻きつけてあったっけ)
とりあえず、付け加える論理式をPとして、Pに含まれる命題変数を一切置換禁止としましょう(Pに含まれる命題変数は他の論理式に出てきても置換禁止)。このように拡大した体系で、論理式Qが導けたとします。それがどういうことかというと、Pを前提として使って(Pを公理みたいに扱って)、Qが導けたということですね。このときに公理系Lで、PならばQが証明できれば、とにかく一瞬だけ(公理系LにトートロジーではないPを付け加えてQを導いたところだけ)お釈迦様の掌から外へ出られたことになります。(一瞬でも何でも、お釈迦様の掌から出られればいいもんね)
これをまとめて、立てた予想を正確に書くと、論理式Pに含まれる命題変数に関しては、全論理式で置換禁止にすると、式(49)が成り立つと予想されます。
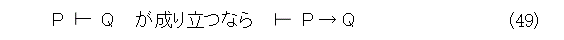
それでは、帰納法を使って、様子を見ながら確かめましょう。帰納法はなかなかよい論法です。まず、最初に簡単な具体例を使って調べますね。次に、ちょっと増えたときに、その差分の推論過程が見える形で調べていきます。このように考えて、証明にだけにしか使わないのはとてももったいないので、色々なところで使いましょう。
まず、Qを導く過程について考えましょう。これは、Pと公理から導かれるので、一番最後がQとなっている論理式の列です。そして、その列に表れる論理式は、Pか公理か、または、推論によって導かれた論理式、つまり、それ以前の論理式から置換(ただし、Pの命題変数に関する置換は禁止)によって得られたものか、それ以前の論理式から、三段論法によって得られたものです。これを念頭に置きましょう。
最初に、論理式が1個だけだったとします。すると、これは、Qだけです。推論は使いようがないので、QはPかLの公理Aのどちらかですね。この頭に「Pならば」を付けます。


式(50)は、式(31)から公理系Lで証明可能です。式(51)も、式(52)のように変形すれば、公理系Lで証明可能であることが簡単に確かめられます。当然、読者の宿題です。

次に、n 個の論理式の場合に、式(49)が成り立っているとして、n + 1 個の論理式を考えましょう。もちろん、この論理式の列はQを導く過程の論理式なので、最後の論理式はQですね。
そうすると、Qは導かれる論理式なので、次の四つの場合のいずれかになります。
(その1) QはP
(その2) Qは公理
(その3) Qはそれ以前の論理式から置換によって推論される
(その4) Qはそれ以前の2個の論理式から三段論法によって推論される
(その1)と(その2)は既にやりました。
(その3)を考えましょう。Qはそれ以前の論理式Rから置換によって推論されるとします。このとき、Rは n 番目以前なので、帰納法の仮定から、PならばRは公理系Lで証明可能です。つまり、式(53)が成り立ちます。

そこで、RをQに変える置換を式(53)に適用すると、この置換はPに含まれる命題変数を一切含まないので、式(53)のRだけがQに変わって、

式(54)が成り立つ。つまり、置換のときは公理系Lで証明可能になります。
最後に、(その4)を考えましょう。Qが、それ以前の、S、SならばQから三段論法によって推論されたとします。つまり、式(55)から三段論法によって推論されたとします。

そうすると、式(55)に出てくる論理式は n 番目以前なので、帰納法の仮定から、PならばS、Pならば「SならばQ」は公理系Lで証明可能です。つまり、式(56)が成り立ちます。
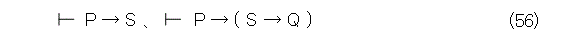
ところで、公理系Lで一般に、式(57)が成り立つ(当然読者の宿題)。
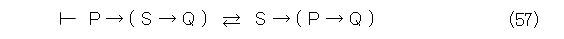
これを使って、式(56)を書き直すと、
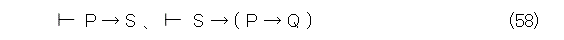
となる。ここで、式(23)を使うと、
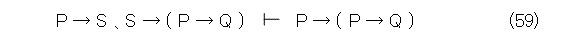
式(58)と式(59)から、

が成り立つ。一方、公理系Lで一般に、式(61)が成り立つ(当然読者の宿題)。
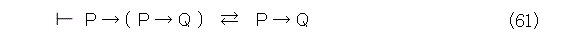
これから、

となって、三段論法のときも公理系Lで証明可能になります。
こうして、n + 1 でも成り立つことが解り、公理系Lで、PならばQが証明できました。
以上から、式(49)が成り立ちます。こうして、我々はお釈迦様の掌から外へ出られました。よっかたね。
なお、式(49)(命題変数に対する置換制限を付ける)のことを演繹定理と呼びます。
4.述語論理
いよいよ述語論理です。命題論理よりも、かなりごちゃごちゃしてやっかいです。
ネットで「述語」を検索すれば、文章を主語と述語に分けてどうとかこうとか、というのが沢山引っかかってきます。とにかく、命題を主語と述語に分けて扱うのだけれども、通常の国語の文章よりもやっかいなことが付きまといます。
大体、ネットの解説サイトでは、例えば「俺は食い意地が張ってる。」というような例で出てきて、「俺」が主語で、「食い意地が張ってる」が述語というような説明です。誰が、とか何がというようなところが「主語」で、状態とか動作とかを表しているのが「述語」と説明されています。日本語では、主語を省略していることが多いため(対偶漫談でも出てきましたね)、既に、面倒を背負い込んで解りにくくなっています。述語がどこにかかるのかを考えなくてはなりませんからね。
ところで、述語論理では、多変数を扱うため、その逆の意味でやっかいなことになってきます。各変数が主語と考えると、主語が多数あって、述語がそれら全部にかかるというような解釈が必要になってきますから。例えば、「アヒルとアイガモは食い意地が張ってる。」という文章を考えてみましょう。主語は、「アヒル」と「アイガモ」ですね。この両方に「食い意地が張ってる」という述語がかかります。とにかくやっかいですね。
さて、命題論理では、論理式の形式的な意味を考えるとしても、内容までは考えずに真偽を考えていました。こんなこともあって、真偽表がお釈迦様の掌になっていました。これにならい、論理式の内容的な意味は考えず、その真偽を扱うことの方が妥当でしょう。
つまり、n 個の主語がある述語Pを以下のように考えます。
n 個体変数の述語Pを、x1 ,x2 ,・・・,xn に対して、その真偽値を対応させるものとする。ただし、各個体変数は、それぞれの個体変数の変域内にあるとする。
要するに、P( x1 ,x2 ,・・・,xn ) は真と偽の2値しか取らない関数(写像)のことです。
そうすると、それはそれで色々とやっかいなことが出てきます。命題論理では、真偽が決まっており、真偽表を簡単に書けましたが、述語論理では、そううまくは行きません。
例えば、1 、2 、3 、の三つを変域として、「x は偶数だ」というのを考えましょう。このとき、x は三つの値しか取らないので、これを全部書き下して真偽を付けます。「 1 は偶数だ」(偽)、「 2 は偶数だ」(真)、「 3 は偶数だ」(偽)となりますね。つまり、取り得る値によって真偽が変わってきます。これはまだ3個しかないので書き下せましたが、変域が無限集合になると書き下せません。こうして、一般的に、真偽表は書けないということになります。
更に、個体変数によって文章が決まっており、その個体変数を変域上で動かしたときにできる文章を束ねていることが解ります。先の例で、「x は偶数だ」は、「1は偶数だ」、「2は偶数だ」、「3は偶数だ」の三つを束ねていましたね。これから、述語論理では、論理式を束ねたもの、いい換えると、論理式の型を扱うものと推測されますね。そのつもりでかからないと痛い目にあいそうです。(命題論理では実体を扱っていた)
次に、述語論理で新たに導入される論理記号について考察しましょう。新たに導入されるのは、以下の二つです。
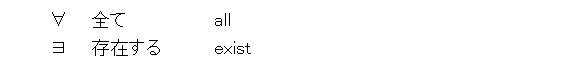
これらは、今までのどの論理記号とも扱いが異なり、優先度がなく、( )がない限り、並んでいるものは左から順に個体変数と結びつきます。また、個体変数を束縛するためのものなので、そのつもりで扱わないといけません。


式(63)は、「全ての x についてP (x) 」と読みます。x の変域Dを明示したい場合は、「Dの全ての x についてP (x) 」とか、「Dの任意の x についてP (x) 」などと読みます。
式(64)は、「ある x についてP (x) 」とか、「P (x) となる x が存在する 」とか、「適当な x についてP (x) 」と読みます。x の変域Dを明示したい場合は、「Dのある x についてP (x) 」などと読みます。
また、式(63)や式(64)の中で x は束縛されているとか、x は束縛個体変数などといいます。それに対し、「全て」や「存在する」という記号に束縛されていない個体変数は自由であるとか、自由個体変数などといいます。
ここで、述語の例を書くために、色々な分野から記号や概念をかっぱらってきます(述語は関数なので、関数を書くには、色々な記号や概念を使った方が解りやすい)。こういうとき、みんな借りてきてとかいいますが、返すのを見たことはありません。
そう、あれは忘れもしないウン十年前のことだった(完全に忘れている)。小学校の引き算で、繰り下がりの話のときだ。例えば、25 − 7 を計算しようとすると、一の位の 5 から 7 は引けないため、最初に、一の位が十の位から 1 を借りる。十の位は 2 から 1 が引かれるので 1 。一方、一の位は十の位から 1 を借りるが、位が一つ上のところから借りたので、実は 10 を借りたことになる。次に、一の位は、借りた 10 から 7 を引いて残り 3 を求め、その 3 をどうするかというと、一の位に繰り込んでしまう。これは、5 に 3 を足して 8 とすることだ。こうして、十の位が 1 で、一の位は 8 だから、そのまま読んで、引き算の結果は 18 。これを計算結果としていた。しかし、一の位は決して借りた 10 を返すことがなかった。
まあ、手元資金が5千万円しかないときに、7千万円の催促がきたら、どっかから1億円借りて支払い、余りの3千万円を手元資金に繰り入れて、手元資金を8千万円にし、借金を踏み倒すのと全く一緒です。まるでどっかの国の悪徳企業がよくやっているような話です。
「借りる」というウソはやめて、正しく「かっぱらってきた」ということにしましょうね。(カツアゲで「借りる」といったら返さないことだから、そういう意味では正しいともいえるが)
元へ戻って、述語は関数だと書きましたが、関数のままだと、やっぱり書きにくいし解りにくいので、関数化のちょっと前で表現することにします。
何をいっているのかというと、 0 を真で、1 を偽として、x = a を表現する述語は、式(65)を使って、式(66)と書けます。
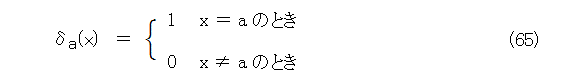

それよりも、x = a を述語とみなした方が解りやすいでしょう。
さて、変域を 1 、2 、3 の三つからなるものとして、述語P (x) を考えます。少し前でやったように、P (x) はP (1) 、P (2) 、P (3) の三つの命題を束ねたものになります。そして、「全ての x についてP (x) が成り立つ(つまり真)」ということを考えましょう。これは明らかに、P (1) が成り立つ(真)、P (2) が成り立つ(真) 、P (3) が成り立つ(真)ですね。したがって、「P (1) かつP (2) かつP (3) 」が成り立ち(真)ます。よって、変域が有限集合であれば、「全て」は「かつ」で表現でき、命題論理から外へ出ていません(またしてもお釈迦様の掌に捕らわれてしまいました)。でも大丈夫だもんね。変域が無限集合のときは、有限個の記号で書き下せなくなって、「かつ」になんか帰着させられないもんね。これを本当の面白さは無限にあるといいます。
同様に、変域を 1 、2 、3 の三つからなるものとして、述語P (x) を考えます。「P (x) が成り立つ x が存在する」ということは、P (1) が成り立つ(真)か、P (2) が成り立つ(真)か 、P (3) が成り立つ(真)かの少なくとも一つが成り立つことですね。したがって、「P (1) またはP (2) またはP (3) 」が成り立ち(真)ます。これも、変域が有限集合であれば、「存在する」は「または」で表現でき、命題論理から外へ出ていません。それでも、変域が無限集合のときは、有限個の記号で書き下せないので大丈夫です。
なお、新しい概念や観点などが出てきたときは、常に、今までの知識と比べ、どこが外へ出ているのかを考えましょうね。(要するに、お釈迦様の掌から外へ出ているかどうかということ)
ここで、ちょっとだけ論理記号の使い方を練習してみましょう。x と y の変域を実数として、原点を中心とする単位円は式(67)と書けます。
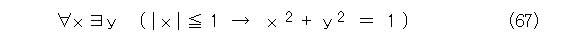
論理記号は使いこなせると便利なので、色々と自分で書いて練習してみましょう。
次に、論理式を考えましょう。命題論理で論理式を定義したときのことから、論理式は、述語変数と個体変数に論理記号を適用していけばよいと予想されます。この予想に従って帰納的に定義すると次のようになりますね。

しかし、この定義によって論理式を書いていくと、例えば、式(68)や式(69)のようなものが出てきてしまいます。


式(68)は無意味ですね。式(69)は個体変数 x が、束縛個体変数になっているところと、自由個体変数になっているところのちゃんぽんになっています。ということは、この論理式の定義はあまりよくないことになりますね。またしても予想は外れましたが気にする必要はありません。外れたら、その修正を考えればいいのです。そこで、もう少し注意書きを付けて複雑にし、式(68)や式(69)のようなものが発生しないようにした論理式の定義を考えることを読者の宿題としましょう。
なお、ここでは、どっかの国でよくやっているように、都合の悪いものは無視し、問題が生じたら「想定外」といってごまかすことにします。
ところで、命題論理のときは、公理化とは関係なく、真偽表があり、そこからトートロジーが定義でき、これが後々重要になってきました。そうすると、述語論理でも、同じような状況が考えられると予想されますね。それなら、これらと同じ概念を用意しておく方が良さそうです。しかし、前に書いたように、変域が無限集合のときは、真偽表が書けないで、真偽表抜きでトートロジーみたいな概念を扱わねばなりません。
まず、述語論理と、命題論理と比べてみましょう。こういう比較は重要です。
命題論理では、命題変数だけでしたが、述語論理では述語変数と個体変数が出てきます。命題変数では、論理式の真偽は、命題変数の真偽から真偽表によって決まりました。そして、真偽表は、全ての命題変数に真偽値を入れて作ったものです。
この真偽の決定方法を述語論理に適用しましょう。変域Dと、論理式Aが与えられたとします。命題論理では、全ての命題変数と、全ての真偽値を使っていました。これは、全ての述語と、変域内の全ての個体と読みかえられます。少しかっこ良くいうと、任意の述語と、変域内の任意の個体です。これに気をつければ、命題論理のトートロジー相当の概念として、「論理式Aが変域Dで恒真」というのを、「述語変数に、変域D上の任意の述語を割り当て、自由個体変数に変域D内の任意の個体を割り当てたときに、つねに真になる」ことと定義できます。
「任意の」とか、「全て」とくれば、今度は、それを「存在する」とか「ある」とか「適当に」と置き換えたものも考えられますね。そこで、「論理式Aが変域Dで充足可能」というのを、「述語変数に、変域D上の適当な述語を割り当て、自由個体変数に変域D内の適当な個体を割り当てたときに、真にできる」ことと定義します。
更に、どんな変域の上でも恒真であるような論理式は「恒真」、なんらかの変域の上で充足可能となるなる論理式は「充足可能」といいます。
少し、恒真な論理式を考えましょう。恒真な論理式は、変域によらないということで、後で出てくる公理と推論だけから出てくるものになります。例えば、式(70)です。

式(70)で、P (x) をQ (x , y) で置き換えてみましょう。このとき、P (y) はQ (y , y) で置き換えられます。そして、

となります。
ところで、変域を 0 、1 として、その上でQ (x , y) を解釈した述語を同じQ (x , y) で表し、
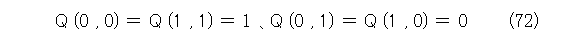
とすれば、式(71)は恒真でないことが解ります。つまり代入によって恒真は崩れます(恒真の定義を読み返すこと)。第1章では、代入を行うに際し、文字の書き換えだけで済まそうとしたら色々と問題が発生するので、( )によって何とか回避しました。しかし、今度はその手が通用しません。
原因を考えましょう。式(70)と式(71)、Q (x , y) をよく眺めると、束縛個体変数と自由個体変数がごっちゃになって使われていることが解ります。この点をよく考えると、束縛個体変数と、自由個体変数をごっちゃににするような代入をしてはいけないということに気づきます。
束縛個体変数と、自由個体変数をきちんと分離しましょう。ここで、論理式Aの述語変数P( x1 ,x2 ,・・・,xn ) に論理式Bを代入するものとします。
まず、論理式Bが x1 ,x2 ,・・・,xn に対応する n 個の自由個体変数を含んでいなくてはなりません。そこで、その個体変数を x1 ,x2 ,・・・,xn と書き換えます。すると、論理式BはB( x1 ,x2 ,・・・,xn ) と書けます。ただし、Bはその他にも自由個体変数を含んでいるかも知れません。ここがミソになります。この上で、以下の条件(1)、(2)が満たされるならば、代入が許されます。
(1) Bに含まれる x1 ,x2 ,・・・,xn の他の自由個体変数は、Aの中で束縛個体変数ではない。
(2) PがAの中で、P( y1 ,y2 ,・・・,yn ) という形で表れるならば、全ての y1 ,y2 ,・・・,yn はBの中で束縛変数として表れない。
ここまで準備して、いよいよ公理化です。基本的に、命題論理の公理に、束縛変数に関する公理を追加すればよいはずですね。しかし、述語論理では、論理式を束ねたもの、あるいは、論理式の型を扱うものなので、公理を束ねたもの、すなわち、公理型となります。また、慣例によって、論理式を表す変数を、超変数と呼びます(論理式変数でもいいと思うが)。

推論規則は、置換と三段論法に束縛記号の導入規則を付け加えたものです。ただし、置換について、代入はこの直前で書いた代入規則を満たす必要があり、また、変数の書き換えを行う場合も含みます。

(3)、(4)で論理式の間にある線は、上の式が成り立てば、下の式が成り立つという意味です。解りやすくするためのもので、実際には書く必要もありません。
また、証明については以下です。

以上のように定式化した体系をLと書くことにします。ちょっと複雑で、やっかいなところはあるけれども、大体命題論理と同じようなことが成り立ちます。
例えば、公理型は恒真であるとか、推論規則によって恒真が保存されることが成り立ちます。簡単なので、読者の宿題です。また、これから、証明可能な論理式は恒真であることが解ります。
ところで、命題論理のときは、トートロジーと証明可能とは同じになっていたこと(真偽表に関して完全)から、恒真であれば証明可能であると予想されますが、今度は、そうそう簡単には確かめられそうもありません。こんなときは、しばらくプラプラしてみるのも手です。(これ、どっかの国でよくやる「先送り」というやつだ)
あと、命題論理では演繹定理が成り立ったので、述語論理でも成り立つと予想されます。実際、成り立ちますが、多少複雑で面倒です。しかし、よい練習なので読者の宿題です(次の章を少し読んでからの方がいいかも)。
5.充足定理
今度は、述語論理で論理式の集合を考えましょう。この集合内の各々の論理式が、ある変域で共通の解釈のもとに真であるとき「充足可能」といいます。つまり、各々の論理式は、述語変数に、変域上の適当に共通な述語を割り当て、自由個体変数に変域内の適当に共通な個体を割り当てたときに、真にできるということです。また、このときに、もとの論理式の集合を、充足可能な論理式の集合ともいいます。
では、充足可能な論理式の集合Mを考えましょう。Mの要素は、ある変域Dで、述語変数に、変域上の適当に共通な述語を割り当て、自由個体変数に変域内の適当に共通な個体を割り当てると真になっています。このときに、Mは無矛盾かどうかを考えましょう。
その前に、論理式の集合Mが無矛盾というのは、公理にMの要素を全部追加したものが無矛盾ということです。忘れた人は第3章を読み返しましょう(第3章では1個追加しただけだった)。
充足可能な論理式の集合Mといっているので、当然ですが、Mは証明可能な論理式の集合とは限りませんね。それで、うっかり追加すると矛盾になってしまいます。第3章では、それを避けるために、置換禁止の処置を行いました。
そのことを念頭に置くと、置換禁止が必要ですね。では、何を置換禁止にすればよいのでしょうか。第3章では、命題変数を一切置換禁止としました。とすれば、まずは、述語変数を一切置換禁止にすることが思いつきます。
しかし、述語論理では、その他に個体変数が出てきます。そうすると、これも一切置換禁止にした方がよさそうです。それで充足可能の定義をよく見てみると、自由個体変数に変域上の適当な個体を割り当てていました。したがって、自由個体変数を一切置換禁止にすればよさそうですが、注意が必要です。述語論理で、自由個体変数を束縛するような推論が導入されていたので、これも禁止にします。つまり、自由個体変数については、一切の置換を禁止し、更に束縛する推論も禁止にします。
これらの処置を、簡単に、述語変数と自由個体変数を「定数とみなす」といいます。
元へ戻って、ここで考えているのは、充足可能な論理式の集合Mに対して、Mの要素に表れる述語変数と自由個体変数を全て定数とみなしたとき、無矛盾になるかという問題ですね。早速、試してみましょう。
述語論理の公理に、Mの全ての要素を付け加えて、論理式Aが証明できたとします。もちろん、これは、Mの要素は公理みたいに扱うけれども、定数とみなした変数の置換は禁止して、推論規則を使うことです。
それで、Aの証明に表れる述語変数と自由個体変数で、Mの要素に含まれるもの全てを、変域Dで、真となるように、共通に割り当てた述語と個体を代入します。このとき、定数とみなしたのに、代入していると考えて混乱する人がいます。推論規則を使う際に定数とみなして置換禁止にしたのであって、解釈禁止としてはいません。この点を、よく読み返して考えましょうね。
とにかく、共通の解釈によって、証明の途中に出てくる論理式は全て真になります(公理はもちろん真だったもんね)。そうすると、Aも真となり、Aは充足可能ですね。ところで、矛盾は偽であり、充足可能になりませんから(充足可能から充足可能しか出てこないから)、充足可能な論理式の集合Mは無矛盾です。
充足可能な論理式の集合は無矛盾となるのが解りました。当然、この逆を考えてみたくなりますね。つまり、無矛盾な論理式の集合は充足可能になるかどうかということです。これは、適当な変域を持ってきて、その上で、述語変数に、変域上の適当に共通な述語を割り当て、自由個体変数に変域内の適当に共通な個体を割り当てたときに、真にできるかということです。
実は、自然数の集合の上で充足できるということが知られています。詳しく書くと、以下の様になります。
「論理式の集合Mに対し、その要素にあらわれる述語変数と自由個体変数を定数とみなしたときに無矛盾であるとすれば、自然数全体の集合の上で充足可能である。」
これは充足定理と呼ばれ、述語論理の入門となるものです。
このままの形で扱うと少々面倒なので、ちょっと制限を付けて、以下の場合で考えましょう。
「閉じた論理式の集合Mに対し、その要素にあらわれる述語変数を定数とみなしたときに無矛盾であるとすれば、自然数全体の集合の上で充足可能である。」
閉じた論理式というのは、自由個体変数を含まない論理式のことです。要するに、もう飽きてきて面倒になってきたので、自由個体変数の部分をサボって手抜きをするということです。まあ、ちゃんと自由個体変数込みの証明が載っている書籍は沢山あるので(手に入るかどうかは知らんもんね)、自分で探してみるとよいでしょう。以下を参考に、自力で証明するなら、なおよいと思います。ちなみに、ヘンキンの「飽和法」というものを使って証明します。やり方が決まっているので、誰がやっても同じような感じになります(以下もこの方法による)。
それでは、閉じた論理式の集合Mに対し、その要素にあらわれる述語変数を定数とみなしたときに無矛盾ということを仮定して考察を進めましょう。
まず、述語論理の体系をLを、次のように修正してL0+ とします。
(1) 述語変数をMの論理式に表れるものだけに制限し、全て定数とみなす。
(2) Lの公理の自由個体変数を全て、「全て」という束縛記号によって束縛する。
(3) Mの論理式を公理として追加する。
(4) 述語変数P( x1 ,x2 ,・・・,xn ) の x1 ,x2 ,・・・,xn のところへ、自然数の代入を許す。
(5) 推論規則として、以下の二つを付け加える。
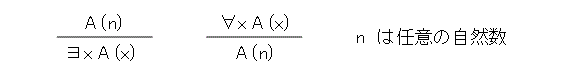
さて、L0+ は無矛盾でしょうか。
とりあえず、L0+ で矛盾が証明できたとします。つまり、式(73)が導けたとします。

それでは、これから何をするかを考えましょう。L0+ で式(73)が証明できたということは、Lで考えると、Mから式(74)が導けるということですね。

そうすると、L0+ 用に修正した部分、つまり、(1)から(5)までが、Lで正当化できればよいことになります。(1)、(3)、(4)は問題ないので、(2)、(5)が正当化できればよいでしょう。これを調べましょう。
まずは、追加した推論規則(5)です。
式(73)で、証明は、有限個の論理式だから、自然数も有限個しか出てきません。これらを証明のどこにも出てこない変数で置き換えます。それを、y1 ,y2 ,・・・,yk (代表で書くときは y )としましょう。もちろん、異なる自然数は異なる変数で置き換えます。そうすると、式(75)の様になります。
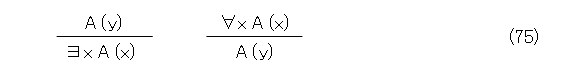
これは、Lの公理(5)と公理(6)のそれぞれに三段論法を適用すれば出てくるので、式(75)はLで正しい推論になります。
次に、(2)です。つまり、Lの公理の自由個体変数を全て、「全て」という束縛記号によって束縛したものがLで証明可能かどうかです。これは、推論規則(4)で、AとBのところに公理を代入すれば、推論規則(4)の下の式が導け、Aは公理であることに注意して三段論法を使えば証明できます。
これで、L0+ での式(73)の証明から、LでMから式(74)が導けた訳ですね。しかし、Mは無矛盾としていたので、これは無矛盾に矛盾します。つまり、L0+ は無矛盾ですね。
次に、論理式を並べることを考えましょう。まず、L0+ で用いる記号は高々可算個です。高々可算個というのは、有限個か、無限個あったとしても、自然数と1対1対応(全単射)が付くものです。まあ、記号といったって、論理記号と、カッコと、変数記号位ですね。これらはせいぜい可算個程度です。
そして、論理式は記号の有限列なので、やっぱり高々可算個です。これは、記号が1個だけのものを1行目に並べ、記号が2個だけのものを2行目に並べ、記号が3個だけのものを3行目に並べ、・・・、以下の様に順序を付けると解ります。図を見てよく考えましょう。
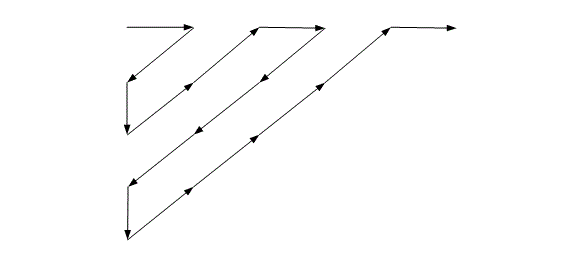
なお、無意味な記号列は飛ばしても差し支えありません。
とにかく、L0+ の論理式を、番号を付けて1列に並べます。そして、番号順に見て行き、式(76)の形をした閉じた論理式を全部取り出し、取り出した順に番号を付け式(77)とします。

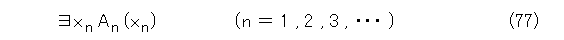
次に、自然数列を作りましょう。
式(78)に表れるどの自然数よりも大きい最小の自然数を i1 とします。

更に、帰納的に、式(79)に表れるどの自然数よりも大きく、かつ in より大きい最小の自然数を in+1 とします。

いま、L0+ に、式(80)を公理として付け加えた体系をLn+ とします。
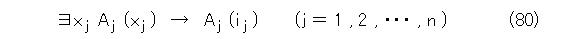
このとき、Ln+ は無矛盾でしょうか。こういうときは、最初に矛盾であると仮定して調べ、それでうまく行かないときは、直接無矛盾であることを調べます。
もし、矛盾であるとすると、Ln+ が矛盾するような n があります。その最小のものを k+1 とします。こういうとき、1個戻ったものに対してどうのこうのと考察するので、最小のものを k とすると k-1 について考察することになり、ちょっと面倒になります。それで最初から k+1 としておいた方が楽です。
さて、仮定から、Lk+ は無矛盾です。そして、式(81)を公理として追加すると矛盾が発生します。
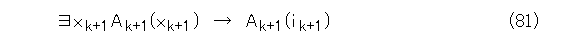
ということは、追加した公理の否定、つまり、式(81)の否定はLk+ で証明可能ですね。式(81)の否定は式(82)です。これは「かつ」で結ばれているので、結局、式(83)と式(84)がLk+ で証明可能になります。
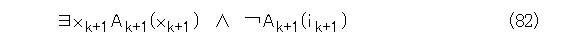


ここで、Lk+ の作り方を見れば、ik+1 はLk+ の公理には表れません。したがって、式(84)の証明に表れる論理式において、ik+1 を証明に表れない変数 y で置き換えてしまいましょう。そうすれば、式(84)の証明は、式(85)の証明になります。

式(85)が証明できれば、前にやった方法を使って、「全て」という束縛記号によって束縛した論理式も証明可能となります。すなわち、

が証明可能となります。
しかし、式(86)は、式(83)の否定ですから、式(86)と式(83)が導けたLk+ は矛盾です。これはLk+ が無矛盾だといってたことに矛盾します。つまり、Ln+ は無矛盾です。
体系の拡大を続けましょう。今度は、Ln+ ( n = 1 , 2 , ・・・ ) の公理を全てL0+ に付け加えた体系をL++ とします。ちなみに、証明は有限個の論理式ですが、公理は有限個などという制限はありません。
さて、L++ は無矛盾でしょうか。仮に、矛盾である式(87)が証明できたとします。

そうすると、証明は有限個の論理式だから、適当なLn+ で式(87)が証明できることになります。しかし、Ln+ は無矛盾なので、やっぱり矛盾します。こうして、L++ は無矛盾であることが解りました。
いよいよ、飽和法を使うときがきました。L++ に論理式を追加して行って飽和させましょう。どのような論理式を追加するかというと下記のような論理式です。

やり方は、まず、自由変数を含まないあらゆる論理式に番号を付けてならべます。それを、C1 、C2 、・・・ とします。そして、更に、L++ をL0++ とおき、以下、帰納的にL1++ 、L2++ 、・・・ と体系の拡張列を作ります。
まず、式(88)のどちらか一方がL0++ で証明可能であるときは、L1++ = L0++ とおきます。そうでない場合は、L0++ にC1 を公理として付け加えたものをL1++ とおきます。

次に、Ln++ まで出来たとして、式(89)のどちらか一方がLn++ で証明可能であるときは、Ln+1++ = Ln++ とおきます。そうでない場合は、Ln++ にCn+1 を公理として付け加えたものをLn+1++ とおきます。

こうして、L1++ 、L2++ 、・・・ と体系の列ができました。この体系列のあらゆる公理をL0++ に付け加えたものをL* とします。
もう解ったと思いますが、新しい体系を作ったら、まず、無矛盾かどうかを考えます。当然、ここでも、L* が無矛盾かどうかを考えます。
L* における矛盾の証明は、有限個の論理式ですから、当然の様に公理も有限個しか使いません。したがって、適当な n があって、Ln++ での矛盾の証明になります。これから、Ln++ が無矛盾かどうかを考えればよくなります。
もちろん、すべての n でLn++ が無矛盾であれば問題ありません。何度もやっているように、こういうときは、そうでないとして矛盾を導きます。
Ln++ が矛盾するような n があるとして、その最小のものを k+1 とします。つまり、Lk++ は無矛盾で、Lk+1++ は矛盾するということです。このとき、Lk++ にCk+1 を付け加えると矛盾となります。つまり、Ck+1 が矛盾となり、その否定はLk++ で証明可能ということです。これは、Ck+1 を付け加えられないことを示しており、Lk+1++ の作り方に反します。
これで、L* が無矛盾ということが解りました。
次に、L* の性質を考えましょう。L* は自由変数を含まない論理式の内、それ自身か、その否定が証明可能となるように論理式を公理として追加したものです。それゆえ、L* では、「自由変数を含まない全ての論理式は、その論理式自身か、その論理式の否定が証明可能」ですね。ちゃんと示すには、今までなんどもやってきた方法を使えばできます(読者の宿題)。
ここまでで、体系としてはできましたので、自然数との接点を探りましょう。自然数が絡んできたのは式(80)です。この式を使うことを考えましょう。
最初は、自由変数を含まない論理式として、式(90)がL* で証明可能であるときに、適当な自然数 n を取ると、D(n) がL* で証明できるかどうかです。

式(77)で、式(90)のような形の論理式は全て番号付けされています。なので、式(90)が k 番目であるとできます。そして、式(91)のように書けます。

L* の作り方を最初から読み直せば、

をL* の公理として追加しているのが解ります。式(91)と式(92)とで三段論法を使えば、

が導けます。つまりD(ik) はL* で証明可能です(要するにD(n) がL* で証明できるということ)。
もちろん、適当な自然数 n に対して、D(n) がL* で証明可能であれば、式(90)がL* で証明可能であることは自明ですね。
以上をまとめると、式(90)がL* で証明可能である必要十分条件は、適当な自然数 n に対して、D(n) がL* で証明可能であることにです。
今度は、「存在する」を「全て」に置き換えて考えましょう。もちろん、式(94)は自由変数を含まない論理式とします。

式(94)がL* で証明可能である必要十分条件は、D(0) 、D(1) 、D(2) 、・・・ が全てL* で証明可能であろうと推定されますね。
式(94)がL* で証明可能なら、D(0) 、D(1) 、D(2) 、・・・ が全てL* で証明可能であるのは自明ですね。この逆が問題になります。
いつものように、D(0) 、D(1) 、D(2) 、・・・ が全てL* で証明可能であるにもかかわらず、式(94)がL* で証明可能でないとします。このとき、その否定は証明可能になるから、式(95)がL* で証明可能になります。

これから、式(96)がL* で証明可能になります。

こうなると、適当な自然数 n に対して、式(97) がL* で証明可能ですね。

そうすると、D(0) 、D(1) 、D(2) 、・・・ が全てL* で証明可能とはなりません。したがって、逆が成り立ちます。
いよいよ最終段階に入るときです。L* の自由変数を含まない証明可能な論理式を、全て真とする述語の集合を作りましょう。
まず、L* の自由変数を含まない証明可能な論理式は以下のどれかです。
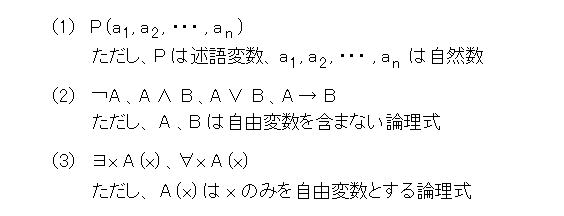
ここで、(1)から(3)の論理式に真偽値を付与しましょう。
最初は(1)です。式(98)がL* で証明可能のとき、P( a1 ,a2 ,・・・,an ) の真偽値を真とします。

そして、式(99)がL* で証明可能のとき、P( a1 ,a2 ,・・・,an ) の真偽値を偽とします。

次に、(2)の論理式は、A、Bの真偽値によって、真偽表を用いて真偽値を付与します。
最後は(3)の論理式です。
式(100)はA(n) が真であるような n があるとき真とし、なければ偽とします。

式(101)は、A(0) 、A(1) 、A(2) 、・・・ が全て真のとき真とし、そうでなければ偽とします。

こうして、自由変数を含まない全ての論理式に真偽値を付与できましたね。
このときに、L* で証明可能な閉じた論理式は、自然数全体の集合の上で真になります。もちろん、L* で証明可能な閉じた論理式の中にはMの論理式が全て入っています。つまり、Mは自然数全体の集合の上で充足可能になります。
さて、充足定理を使うと、先送りにした問題が解決します。これは、第4章の終わりに書いてある通り、「恒真な論理式は証明可能か。」という問題です。
まず、Aを恒真として、充足定理が使えるようにしましょう。充足定理では、自由変数を含まない形だったので、そのように変形しましょう。それには、Aの自由変数を「全て」で束縛することです。この束縛したものを、A* とすれば、A* も恒真ですね。
いつものように、A* をLで証明可能ではないとしましょう。そして、A* に含まれる述語変数を定数とみなします。このときに、式(102)が述語論理の公理と矛盾しなければ(つまり無矛盾)、式(102)は自然数全体の上で充足可能になります。ところが、A* は恒真なので、矛盾ですね。

一方、式(102)が述語論理の公理と矛盾したとすると、式(102)を公理として付け加えて、矛盾した体系ができます。矛盾していると、全ての論理式が証明可能になるので、当然、A* が証明可能ですね。そうすると、演繹定理によって、式(103)がLで証明可能になります。

式(103)を変形するとA* 自身なので、LでA* が証明可能ということが解りました。これは、A* がLで証明可能でないとしていたことに矛盾します。
いずれにしても矛盾が生じます。これで、A* がLで証明可能であることが解りました。
A* がLで証明可能であれば、当然、AもLで証明可能ですから、「恒真な論理式は証明可能。」ですね。
6.コンパクト性定理
ここでの目的は、「こんなこともできないのか。」という限界を知ることです。具体的には、「自然数の上で、どんな公理系を用いても、不等号を完全に特徴付けられない。」という、有名な事実を見ます。そのために用いるのがコンパクト性定理です。
コンパクト性定理というのは以下です。
「論理式の集合の、いかなる有限部分集合も充足可能であれば、元の集合自身が充足可能である。」
これ、論理式の集合の要素(論理式)で、述語変数と自由個体変数を全て定数とみなすと、無矛盾か矛盾かのどちらかになります。
もし、無矛盾なら充足可能であるから問題ありませんね。(本当はサボった方が必要)
そうすると、矛盾のときにどうなるかです。矛盾すれば、矛盾が導けます。まあ、何度も書いてますが、矛盾というのは、以下の式(104)です。

そして、式(104)を導くのに、有限個の論理式しか使いません。そうすると、その有限個の論理式を要素とする集合を考えれば、「いかなる有限部分集合も充足可能」と矛盾しますね(矛盾だと充足可能にならない)。
こうして、コンパクト性定理の成り立つことが解りました。
さて、問題となる不等号についての考察をはじめます。自然数の上で、不等号を定義付ける公理系を用意しましょう(どんなものでも可)。もちろん用意するのは読者の宿題です。
そして、a < b という述語を考えます。正しくは関数表現を行う必要があるけど、以前にも書いた通りそこまではしません。この上で、以下に記載の論理式の集合を考えましょう。

明らかに、この内、どの有限個を取っても、自然数全体の上で充足可能ですね( x に有限個の式に出てくる一番大きな自然数よりも大きな自然数を割り当てればいいから)。
すると、コンパクト性定理によって、式(105)の全体が自然数全体の上で充足可能になります。ということは、式(105)全体の解となる自然数があるということです。つまり、どんな自然数よりも大きな自然数があるということですね。
こうして、どんな公理系を用いても、不等号を完全には特徴付けられないということが解ります。とんでもないですね。
7.おわりに
今回は、第100話ということで、入門までを体系化して書いてみようという企画でした。案の定、途中で飽きてしまいました。こんなことなら、途中で分けて、何回かの連載にした方がよかったような気もします。
また、今回の企画に先立って、第100話は、「こんなこともできないのか。」というとんでもない結論に至るものにしようということがかなり前から予定されていました。もちろん、複雑な内容のものが「できない」というのでは、あまり衝撃にはなりません。簡単で解りやすく、常識と思っていたことが裏切られるようなものの方が面白いと考え、それには、「自然数の上の不等号が完全には特徴付けられない。」という話が丁度よいのではないかと思い選びました。多少はみなさんの刺激になったでしょうか。
完
平成29年6月10日
著作者 坂田 明治(あきはる)
|