|
第102話
行列の固有値について考えよう
|

「主な対象読者」
今回は行列のことを勉強した人が対象です。具体的には、行列の固有値を天下りな方法で教わるのではなく、例えば、このような理由から出てくるという具合に、出てくる理由を楽しみたい人たちが対象です。
本 文 目 次
1.はじめに
2.行列と2次形式
3.動径と法線
4.曲線の勾配
6.おわりに
著者 坂田 明治
第102話 行列の固有値について考えよう
1.はじめに
今回は行列の固有値の話です。行列とか、線形代数(線型代数と書く人もいる)の勉強をすると、必ず出てくるのが固有値です。そして、固有ベクトルがどうとかで、対角化とか、三角化が出てきて、2次形式がどったらこったらで、・・・、はいおしまい。となります。こんなんでいいのか。
天下り的なやり方をやめて、固有値を導入する方法を考えましょう。ここでは、2次形式から固有値へ入って行くやり方にします。この他、どんな導入方法が自然で解りやすいかは、読者自身で考えましょう。
2.行列と2次形式
まず、面倒なので、2次の正方行列しか考えないことにします。
さて、行列は1次式と密接に関係していました(第101話に書いてあります)。これは、式(1)を式(2)のように書いたのだから同然のことです。


ところで、式(2)では、変数である列ベクトルを行列の右からかけていました。しかし、行列には左からかけることもできます。この際に、列ベクトルのままではかけられないので、行ベクトルにしてかけます。ただ、左からかけただけだと、1次式のままなので、行列に左右両方からかけてみると式(3)のようになります。このような、2次の同次式を2次形式と呼びます。単に2次式といった場合は、1次の項や定数項の入ってる可能性があり、注意が必要です。
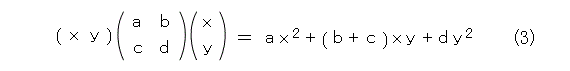
式(3)を定数 t とおけば、式(4)のような2次曲線の式になりますね。
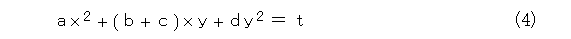
ここで注意というほどのことではないけれども、式(3)で b と c を入れ換えても右辺は変りません。それどころか、 b と c をどちらも、足して半分にしたものに置き換えても右辺は変りませんね。ただし、いずれの場合も、左辺の行列は変ります。つまり、2次形式が同じでも、それに対応する行列は色々あるということです。
当然、一番都合のよいものを考えるということも問題になりますが、それは読者の宿題です。
3.動径と法線
2次式(2次形式とは限らない)は色々なところで出てきます。例えば、物理で、運動エネルギーなどがそれです。そして、よく、運動エネルギーと位置エネルギーの和が、一番簡単になるような座標系を選びます。そもそも、複雑なままだと、面倒くさいし、直感的に把握できないもんね。
まあ、そういう事情があるので、「2次形式イコール定数」とおいて2次曲線とし、その2次曲線の式をできるだけ簡単に表記する座標系を考えてみましょう。
こういうときは、2次曲線の代表として楕円で考えて、当たりをつけましょう。第95話を読まれた方は、これが妥当であると解るでしょう。
式(4)を楕円だと思って、一般的に書くと、図1のようになります。
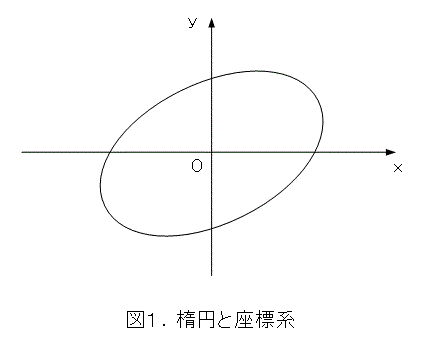
なんか、見るからに楕円の方程式が複雑そうです。
しかし、楕円の長軸と短軸(うまい具合にこれらは直交している)上に座標軸を取ると、図2のようになります。ちなみに、これら、長軸と短軸を合わせて主軸と呼びます。
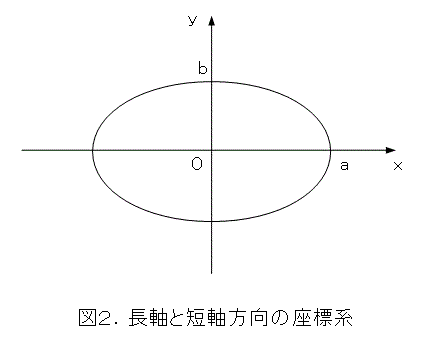
このときは、楕円の方程式も簡単で、式(5)のようになりますね。

そうすると、長軸と短軸を見つけることができれば、方程式を簡単にできるということになります。では、どうやって探しましょうか。とりあえず、楕円を眺めてみることです。何か気づくかも知れません。
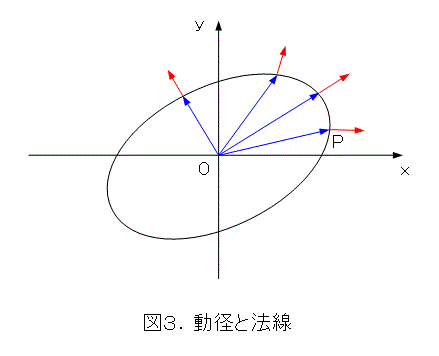
図3のように、楕円上に任意の1点Pを取ります。そして、動径OPと点Pで楕円の法線を考えましょう。Pを色々動かすと(だから動径というんだ)、大概の点では、動径OPと法線は、かくんと折れていますが、長軸と短軸のところでは、同じ向き(逆向き)になること(平行になるという)が解るでしょう。
つまり、長軸と短軸のところで、動径ベクトルは法線ベクトルの何倍かになります。ということは、式(6)のように書けるということです。

更に、P ( x , y ) とすれば、式(7)のようになります。

あとは、法線ベクトルが解れば、楕円の長軸と短軸は求まりますね。
4.曲線の勾配
ここでは、当たりを付けるため、かなり荒い方法を取ります。厳密なやり方が好きな人は、精密に評価してキチンとやりましょう。ためになります。
まず、式(4)の左辺を f ( x , y ) とおきます。つまり、式(8)です。
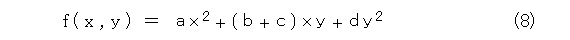
すると、式(4)は式(9)のようになりますね(ここでは左辺と右辺を入れ換えた)。このように書くと、いかにも一般的に曲線を扱うように見えます。(実は、2次式を書くのが面倒なので、サボってるだけ)

さて、法線について考えましょう。といっても、式(9)でどうすればいいのでしょうか。こんなときは、とりあえず変数をちょっと動かしてみるのが常套手段(じょうとうしゅだん)です。ここで、t は x と y の関数のように見えるので、 x と y をちょびっと動かすと、t もちょびっと動くと考えられますね。ここで、x と y をそれぞれ h 、k だけ動かして、そのときの値が、s になったとしましょう。つまり、図4と式(10)です。
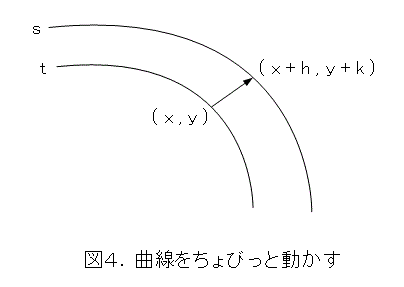

次に、どの位動いたか見ていきましょう。それには、式(10)から式(9)を引けばよいでしょう。
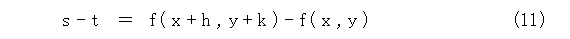
以下、この式の変形を考えましょう。変数が2個もあって解り難いので、途中に片方の変数だけ動いているものを入れます(実際には入れて引くので式の値は変わらない)。
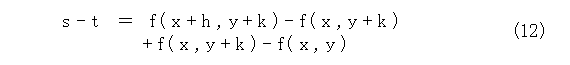
ここで、微分の意味を思い出しましょう。式(13)は、両辺を h で割って、極限を考えれば等しくなりますね。そういう意味で、式(13)は、h が微小のときの近似値になるという意味です。
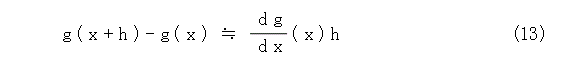
ということから、式(12)の右辺の一行目と二行目は、微分を使って近似できます。ただし、一行目は x で微分し( y を定数とみなして x で微分する)、二行目は y で微分します( x を定数とみなして y で微分する)。慣習に従って、偏導関数記号を使いましょう。すると、式(14)のようになります。
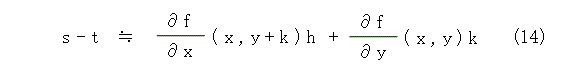
更に、k はちょびっとなので、式(14)の右辺の第1項の値はほとんど変わらないから、無視して、式(15)のようになります。
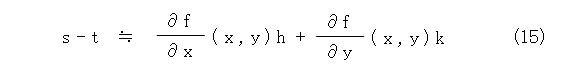
式(15)の左辺を式(11)の右辺で置き換えて、式(13)と見比べましょう。なんか気になりますね。この微分係数相当の部分を、式(16)のように書いて、勾配とか、グラジエント(gradient)と呼びます。ちなみに、式(16)の左辺は、グラジエント f とか、f のグラジエントと読みます。
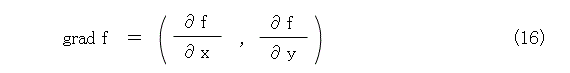
微分係数が、接線と関係が深かったことを思い出しましょう。そうすると、グラジエントも接線と関係が深いと予想されますね。
それでは、接線について考えてみましょう。ある点での接線というのは、その点からちょびっとしか動いてない曲線上の点を取り、その点と、このちょびっとしか動いてない点を通る直線を考え、ちょびっとを 0 に近づけたときの極限でしたね。
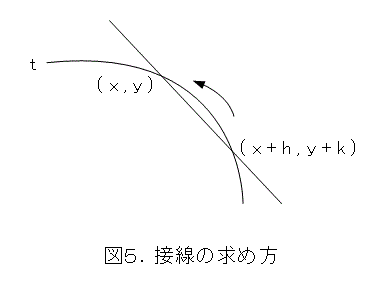
このとき、ちょびっとしか動いてない点も、元の曲線上にあるので、式(10)の s は t のままですね。つまり、等しいということです。したがって、式(15)の左辺は 0 です。左辺と右辺を入れ換えて書き直すと、式(17)のようになります。
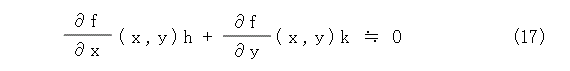
式(17)から k / h を求めましょう。
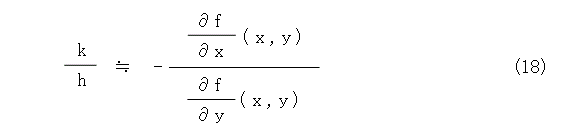
よく考えたら、h は x の増分で、k は y の増分なので、k / h の極限はd y / d x ですね。ということで、極限以降によって式(19)が出てきます。
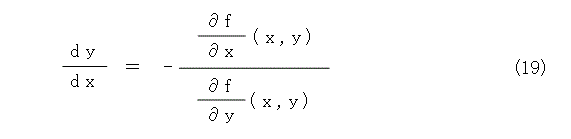
点 ( x , y ) の接線上の任意の点を ( X , Y ) とすると、接線の方程式は式(20)のようになります。
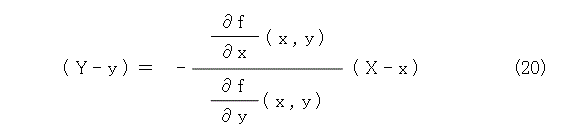
右辺に項を集めて、分母を払いましょう。
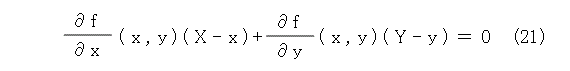
式(21)をよく見ると、grad f と ベクトル( X - x , Y - y ) の内積が 0 になっています。
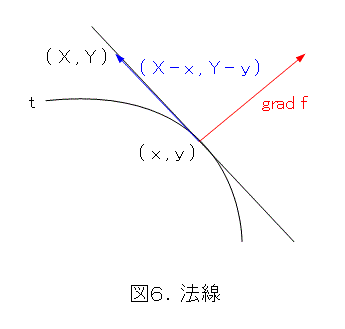
これから、grad f は接線に垂直となり、要するに法線となります。これで法線が求まりました。
5.固有値と固有ベクトル
それでは、式(16)と式(8)から、法線ベクトルを求めましょう。この際に、ベクトルの方向だけが問題なので、大きさはどうでもよくなります。
最初に、式(8)から、式(22)が出ます。
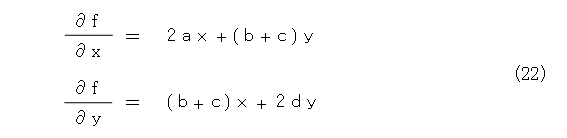
しかがって、法線ベクトルを列ベクトルの形で書くと式(23)となります。
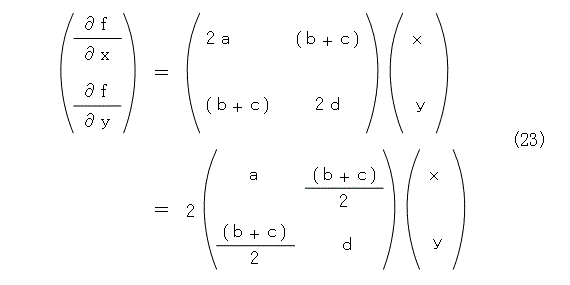
次に、式(23)を式(7)へ代入し、k / 2 をあらためて k とおけば、式(24)のようになります。
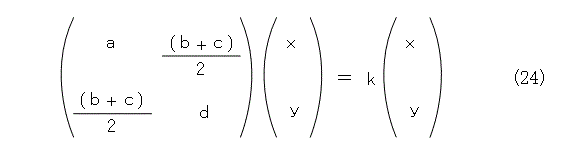
これで、行列の固有値を求めることが、実は、2次曲線をできるだけ簡単な表現にするということと密接に関係しているということが解りました。めでたし、めでたし。
と喜んではいけません。そもそも、式(24)の行列は、式(2)の行列と異なっています。どうしよう。
こういうときは、冷静に考えて、キチンと対処しましょう。間違っても、どっかの国の総理がやるように、証拠をあげられても、しらを切り通してごまかすようなことをしてはいけません。なお、間違いが起こることへの注意を、ちょっとづつ書いていますが、気が付きましたか。
まず、同じ2次曲線になる行列は多数あります。しかも、2次曲線では、主軸は直交しています。ということから、ここでやった方法は、式(24)にあらわれるような行列(これを対称行列という)に対しては、固有値、および固有ベクトルを求めることが、2次曲線の簡単な表現と結びついているということです。そして、このときは、固有ベクトル方向に座標系を取ると、実は、行列の表現も簡単になります(対角行列になる)。対称行列では固有ベクトルが存在し、しかも直行することや、それでうまく対角化できることは、読者自身でやってみましょうね。
そうすると、今までやったことは、行列の固有値と固有ベクトルから、行列の表現が簡単になるということの一例と考えられます。
これから言えることは、より一般的に、式(25)のような、行列の固有値と固有ベクトルを求めることは、やはり表現となんらかの形で関わっている可能性があるということです。
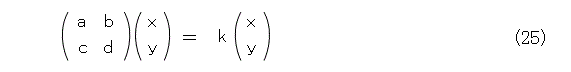
一般に、行列の固有値はあるかどうか解りません。また、あったとしても、固有ベクトルが直行しているという保障もありません(一般的に斜交座標になる)。この辺のことは読者自身で考えましょう。
6.おわりに
第99話、第100話で予想を外すということをちょっとだけやりましたが、今回は、それらに関連して、人の話を鵜呑みにすると危険だという例です。
毎回何度も書いていますが、どんなことでも一応は疑い、自分でよく考える習慣を身に着けましょう。今回は、途中でバレるようなことをちょこっと書きましたが、もっと巧妙に、一例、あるいは特殊な例だけで、さも、一般的に意味があるようなことを書くこともできます。
パラドックスが正しそうな前提と、正しそうな推論で、変な結論に導くのとは別に、一例、あるいは特殊な例で、一般的にうまく行くような結論に導くのは、実はよくある話です。「なんとかなんとかの成功体験」とか、「こうやれば儲かる」なんて類(たぐい)のものが沢山あるでしょう。誰でも、見たことや聞いたことがあると思います。
これらは、まるっきりインチキなものもありますが、実際、それで成功した人の体験ということもあります。しかも、大概の場合、真似してもうまく行きません。それもそのはずです。一例とか、特殊な例は一般的なことではありません。だから、他人の成功話を聞くときは、参考として聞くにとどめ、自分でよく考えた方がよいと思います。この点、本稿を読まれた方はどうお考えでしょうか。
完
平成30年6月18日
著作者 坂田 明治(あきはる)
|