|
第104話
三平方の定理の拡張について考えよう
|

「主な対象読者」
今回は三平方の定理について多少なりとも興味のある人が対象です。三平方の定理を拡張する試みを通して、着目する点によって拡張の仕方が色々あることを知り、場合によっては、全く異なる分野と関係してくるということを実感する試みです。
本 文 目 次
1.はじめに
2.三平方の定理
3.図形の拡張
4.立体図形への拡張
5.射影との関係
6.おわりに
著者 坂田 明治
第104話 三平方の定理の拡張について考えよう
1.はじめに
今回は、三平方の定理の拡張について考えてみましょう。
まず、三平方の定理は、とても役に立つ定理です。例えば、テントや、ビニールハウスを建てるときなどで、四隅を直角にするときに使います。実際にやったことのある人も多いと思いますが、どうでしょうか。
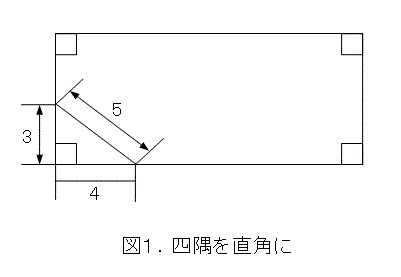
例えば、図1のように、隅で長さが3と4と5の紐を使って三角形を作ります。すると、図のように直角ができます。角度を直接扱うより、長さを扱った方が簡単なため、このやり方はとても重宝します。
よく、目分量でやって、いびつなものを作る人がいますね。いびつだと壊れやすいので、目分量で作ろうとせず、直角を出すようにした方がよいと思います(そういえば、いくら失敗しても目分量でやる人もいたなぁ)。
2.三平方の定理
以下、特に断らない限り、主に三角形は直角三角形、座標は直交座標とします。その他、手抜きで描かれていることもあるので、適当に判断して補いましょう。(理科好き子供の広場では、自分で考えることを主体とするため、読者が考えて補うことを推奨しています)
さて、三平方の定理は図2にあるとおりです。
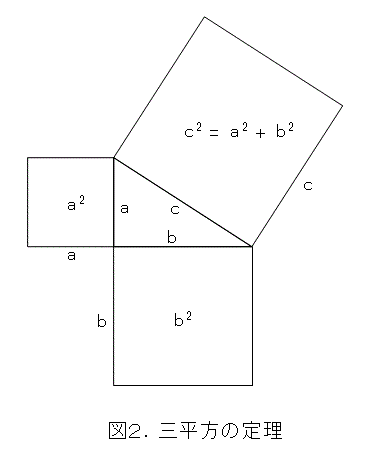
三角形の直角を挟む辺に乗っている正方形の面積の和が、斜辺に乗っている正方形の面積に等しくなります。
三平方の定理は、何通りあるのか解らないくらい沢山あります。例えば、図3の証明方法です。これ、確か、バスカラというインドの数学者がやった証明方法だったと思います。この図を見せて「見よ。」とだけ言っていたと思います。ちなみに、絵だけ描いて、説明しないという手抜きでよく使われます。
ちなみに、「分かる」というのは、善と悪に分けるとか、ものごとを二つに分けるなどの分離が語源であり、本稿などでは、考えて理解するという意味を強調したいので、あえて「解かる」と書いていますので、あしからず。
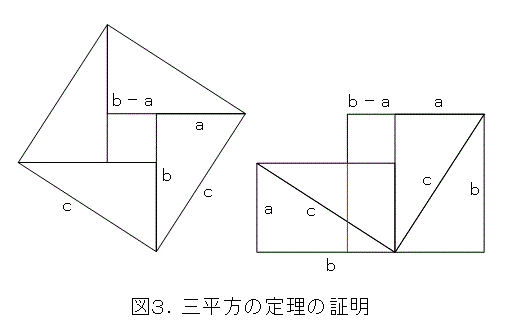
三平方の定理は、色々な使い方ができます。直角を出すときに使うほかに、例えば、直角を挟む辺の長さから、斜辺の長さを出すという使い方です。
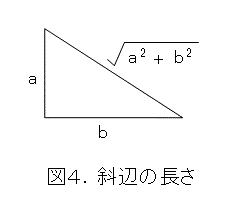
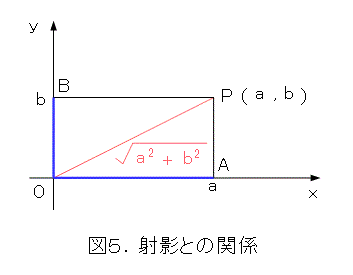
また、座標絡みでは、線分OPを x 軸と、 y 軸に射影すると、各座標軸に射影した線分の長さの2乗の和の平方根が線分の長さに等しくなります。大したことはないと思うかも知れませんが、それは後のお楽しみです。
3.図形の拡張
では、次に、三平方の定理の拡張について考えましょう。拡張するときは、どこに着目して拡張するのかを考える必要があります。この章では、三角形の辺に乗っている図形の拡張を考えます。
図6はヒポクラスの定理と呼ばれているものです。なお、各辺に乗っているのは半円です。
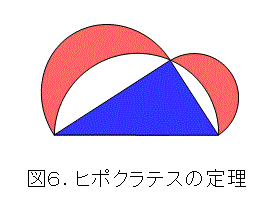
赤い部分の面積の和が青い部分になるというものです。一見すると、面倒くさそうな気がしますが、斜辺に乗っている半円を折り返すと簡単になります。
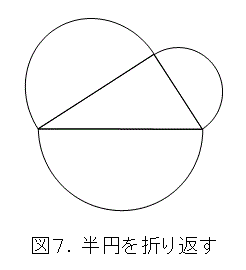
半円の面積は簡単に計算できるので、ヒポクラスの定理はすぐに証明できるでしょう。読者の宿題です。
また、これに関連して、図8のようなものもあります。確か、ユークリッド原論に載っていたと思いますが、手元にユークリッド原論がないため確認できません。
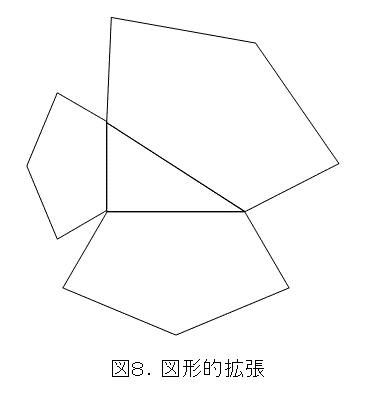
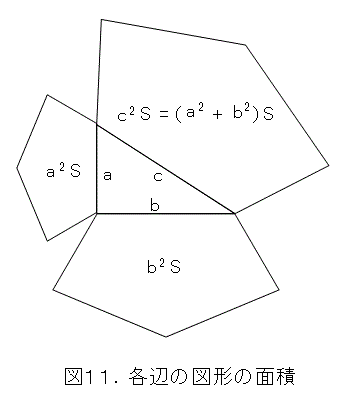
各辺に乗っている図形(辺を1辺とする図形ということ)が全て相似であるときに、直角を挟む辺に乗っている図形の面積の和は、斜辺に乗っている図形の面積に等しくなります。
これは、相似比から面積比が出せれば簡単に証明できます。ただし、ヒポクラスの定理で見たように、多角形だけではなく、もっと一般の図形についても成り立ちます。
まず、正方形の場合に、相似比が 1 : r (つまり r 倍)のときに面積比がどうなるかを考えましょう。
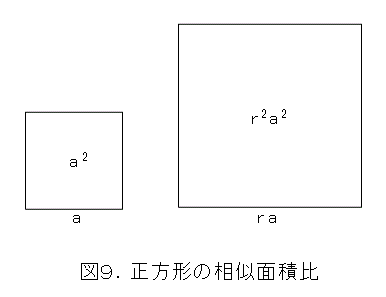
図9を見れば、面積比は、 1 : r2 ですね。これが解れば、一般の図形でも簡単です。
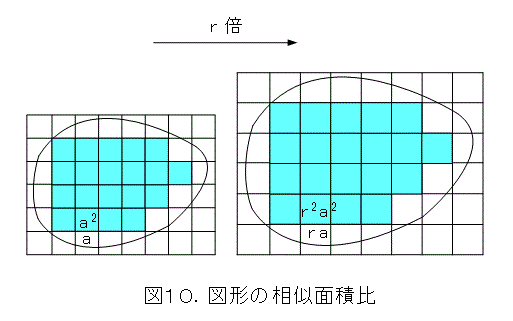
一般の図形は、図形の内部に入っている正方形の面積の総和で面積を近似します。するとそれを r 倍すればいいだけですから、近似した面積は r2 倍になります。それから、一般の図形についても、面積比が 1 : r2 と解ります。
面積比が出たので、あとは簡単に証明できるでしょう。当然、読者の宿題です。
4.立体図形への拡張
今度は、次元を上げて、立体図形への拡張を考えましょう。
最初に、直角三角形に相当する空間図形を考えなくてはなりません。三角形に相当する空間図形が三角錐であることに異論はないと思います。問題は、直角の扱いです。直角に関わる記述があり、かつ、基本的となるものは、「直角三角錐」と「直辺四面体」でしょう。(これ等の言葉は相当古い教科書じゃなくては出てこないから、詳しく知りたい人は、結構な年寄りに聞いた方がよいと思う)
まずは、直辺四面体から。直辺四面体というのは3組の対辺が垂直である四面体です。例えば、正四面体です。これ、正三角形を4枚張り合わせたもので、この場合、正三角形の空間化と考えた方が自然でしょう。こういうものまで含むと、概念が広すぎて、あまり直角とは関係ないかも知れませんね。ひとまず、このままにしておきましょう。
次に、直角三角錐を考えましょう。これは、1つの三面角が直角のみからできている三角錐です。
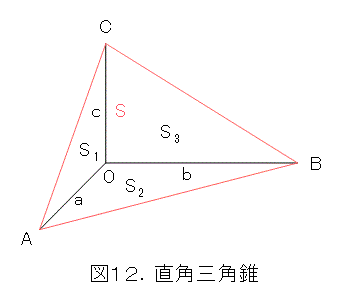
図12で頂点Oが直角のみからできています。更に、図12をよく見ると、三組の対辺が垂直になっています。ということは、直角三角錐は直辺四面体になっているということです。やはり、直辺四面体では概念が広すぎました。
では、 直角三角錐で考えるとして、三平方の定理をもう一度よく見ましょう。
「三角形の直角を挟む辺の2乗の和が、斜辺の2乗に等しい。」
辺の空間化は面と考えて、直角三角錐へ解釈しなおしますが、言葉で書くと面倒なので、数式で書きます。

今のところ、式(1)は予想です。本当にそうなっているかどうかは、各面の面積を計算して確かめられます。
直角三角形の面積はすぐに計算できますね。
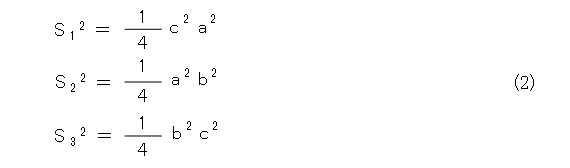
これから式(3)が出ます。
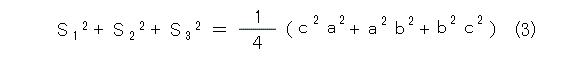
あとはSを計算するだけです。そのために座標を導入しましょう。
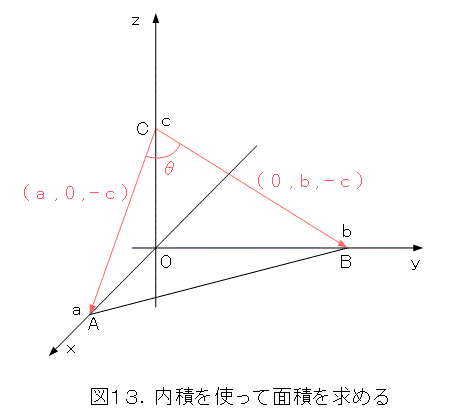
とりあえず、図13のようにします。すると、以下のように計算できます。
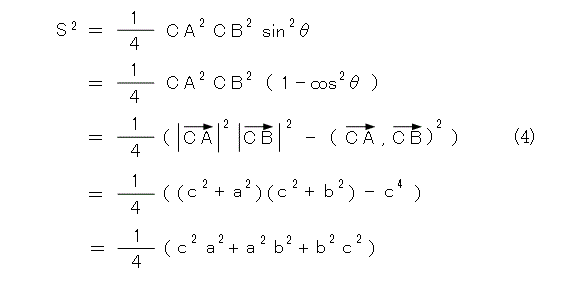
これで式(1)の成り立つことが確かめられました。
以上から、三平方の定理は、直角三角錐の上に拡張できたことになります。
5.射影との関係
さて、図5で射影との関係を描きました。つまり、線分を x 軸と y 軸へ射影すると、射影先の線分の長さの2乗の和が、元の線分の長さの2乗となります。これを空間で描いたものが図14です。
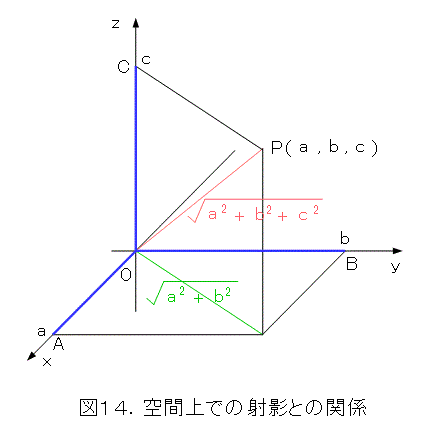
ここで、第4章で考えたように、空間への拡張に際して、辺の空間化を面とする拡張を考えます。
まず、直角三角錐と、射影との関係はどうなるでしょうか。図12を見れば、直角三角錐の斜面(図12の赤い線で挟んだ面)を、それぞれ zx 平面、 xy 平面、 yz 平面に射影したものが、Oを直角としている直角三角形群です。そして、射影先の面の各々の面積を2乗して和をとると、元の斜面の面積の2乗となるというのが第4章の結果です。
では、これを図14の形にして考えましょう。
三角形では、面積計算に余計な係数が付いて煩わしいので、平行四辺形で考えます。
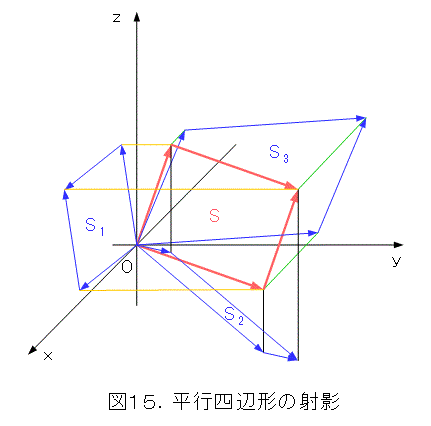
原点を視点とするベクトルを考えれば、それによって平行四辺形が定まります。そうして、平行四辺形を それぞれ zx 平面、 xy 平面、 yz 平面に射影します。
このときに、式(5)が成り立つでしょうか。

平行四辺形の面積を計算するために、原点から出ている2本の赤い矢線で書いたベクトルを、それぞれ、( a1 , b1 , c1 )、( a2 , b2 , c2 )とします(どっちのベクトルがどっちの成分でもよい)。
こうすると、zx 平面、 xy 平面、 yz 平面への射影は以下のようになります。
( a1 , 0 , c1 )、( a2 , 0 , c )
( a1 , b1 , 0 )、( a2 , b2 , 0 )
( 0 , b1 , c1 )、( 0 , b2 , c2 )
このとき、S2 は式(4)と同様にして、
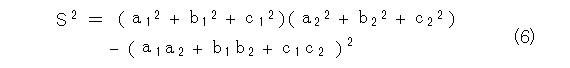
となります。
一方、S12 , S22 , S32 を計算すると、
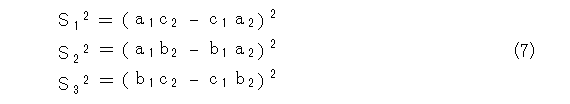
となります。
式(6)と式(7)とから、式(5)の成り立つことが示せますね。
ところで、式(6)と式(7)の右辺を見比べると、
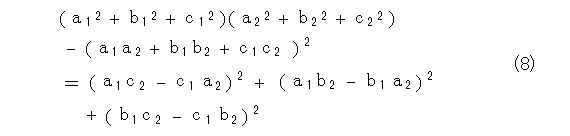
あるいは、ちょっと移項して、
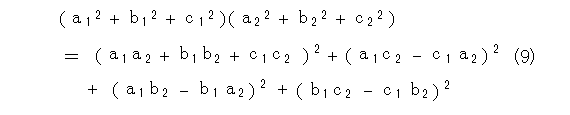
となります。
なっ、なんと、式(8)や式(9)はラグランジュの等式になっています。つまり、三平方の定理を空間へ拡張し、平行四辺形と射影に着目したものはラグランジュの等式だったのですね。
6.おわりに
今回、三平方の定理を基に拡張を考えました。その過程で、どこに注目して拡張を考えるかで、色々と違った世界が出てきました。そして、拡張を考えていくと、今まで考えもしなかったものが、意外な形で結びついてくることがあるというのを見ました。
このように、どこかに注目して考えることは重要です。注目している点から、何かが得られるかも知れません。仮に、何も得られなかったとしても、思考訓練にはなっています。そして、これこそが最も重要なことです。この点、本稿を読まれた方はどうお考えでしょうか。
完
平成31年3月23日
著作者 坂田 明治(あきはる)
|