第１０５話

　根号について考えよう

　

「主な対象読者」

今回は平方根ついて多少なりとも興味のある人が対象です。複素数の平方根を求め、平方根号へ拡張する試みを通して、視点によって結果がかなり変わってくることを知り、他の視点からながめるということがいかに重要化ということを実感する試みです。

　

　

本　文　目　次

　１．はじめに

　２．簡単な問題

　３．２次方程式の解の公式

　４．極形式による表現

　５．複素数の平方根

　６．おわりに

　

著者　坂田　明治

　

　

　

第１０５話　根号について考えよう

　

１．はじめに

　今回は、根号について考えてみましょう。

　

　時々、試験で複素係数の２次方程式を解く問題が出るようです。まあ、この手の問題は必ず解けるように作られているので、色々と式変形を駆使すればなんとかなります（これを受験テクニックというのですね）。

　

　でも、人によっては、反射的に、２次方程式の解の公式を使い、根号の中の複素数をみて、「どっ、どうしよう。」と青い顔になったりします。そもそも、２次方程式の解の公式は、係数が複素数のときにも使えるのでしょうか。もし、使えるとしたら、根号の中が複素数であるときに、どう考えればよいのでしょうか。この辺を考えていきましょう。

　

　

２．簡単な問題

　こういうことを考えるとき、まずは、答えのわかっている簡単な例から考えていくのが常道です。次の式（１）を考えましょう。

　

　

　この方程式の解は、 1 、 - i ですね。しかし、式（１）を展開して、式（２）の形で出題されたらどうでしょう。ちょっと解かり難くなりましたね。受験テクニックで鍛えた人なら、たちどころに因数分解して式（１）とし、解を出すでしょう。

　

　

　ここで、２次方程式の解の公式を適用したらどうなるでしょう。

　

　

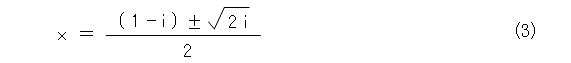
　機械的に解の公式を適用すると、式（３）のようになり、複素数の根号が出てきます。こういうところで、「どっ、どうしよう。」なんて顔をしていると、「ちゃんと理解せず、棒暗記したものを使っているからだ。」とか偉そうに言う人がいます（言ってることは間違っていないけれども）。

　

　まあ、このような連中（偉そうなことを言うだけで、なんの役にも立たない奴）のことは無視して、先へ進めましょう。

　

　今回の目的は、複素数の根号、つまり複素数の平方根号を考えることです。そのため、あえて２次方程式の解の公式を機械的に使用しました。

　

　ここで、もし、２次方程式の解の公式が、複素数を係数とするときも使えるとするなら、式（３）は、 1 、 - i になるはずです。

　

　

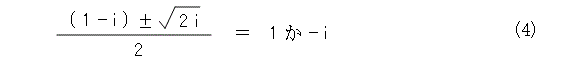
　そして、式（４）を無理矢理解くと、次のようになります。

　

　

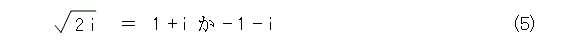
　式（５）から、どうやら、複素数の平方根も、一方を a とすると他方は - a と書けるようですね。つまり、 2 i の平方根は、 1 + i と、 - 1 - i です。どちらを平方根号として取ればよいのでしょうか。

　

　この際に、実数では根号規約があったことを思い出しましよう。 a の平方根は、 a が 0 以上のときは、２乗して a になるもののうち、 0 以上の方を、

　

　

と書きます。

　

　そして、 a が負のときは（ - a となってるのは、根号の中身を正にするため）、

　

　

と書きます。

　

　実数のときは、このような根号規約があります。そこで、複素数の平方根号を考える際には、根号の中身がたまたま実数になった場合に、実数での根号規約が成り立っていなければなりません。つまり、一般的な文字を含む形で平方根号が書かれ、その文字に数値を当てはめたときに、たまたま実数であれば、実数の根号規則を満たすということです。

　

　このようなときは、まず、答えが解かってるものか、あるいは、なんとなく、これが答えになるかなー、という例を考えて確かめるものです。式（８）で試してみましょう。

　

　

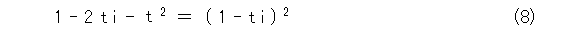
　式（８）の平方根を考えると、式（９）か、式（１０）のどちらかになるだろうと予想が付きますね。

　

　

　

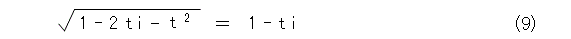
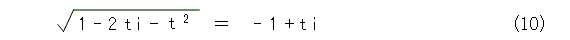
　そこで、 t を 0 とおいてみましょう。すると、それぞれ、式（１１）、式（１２）のようになります。

　

　

　

　式（１２）は根号規約に反するのでダメです。すると、式（９）の方をとればいいかなー、と予想が立ちます。したがって、式（９）を取るような基準を考えていくことが目標となりますね。

　

　

３．２次方程式の解の公式

　さて、とりあえず、複素数係数の２次方程式でも解の公式が成り立っているとして使いましたが、これ本当に大丈夫でしょうか。ここから考えていきましょう。

　

　こういうときは、実際に解いてみるとはっきりします。つまり、解く過程で、実数でなければならないことを使っているかどうかをみていけばよいのです。

　

　まず、２次方程式を一般形で書いた式（１３）を用意します。もちろん a は 0 ではありません（いつものことで、以後、この手の文字に対する制限は書きません）。

　

　

　式（１３）の解の公式を求める方針は、 x の関わる項をひとまとめにして２乗の項を作り、残りの係数項を無理矢理なんかの２乗とみて、式（１４）のように因数分解をします。

　

　

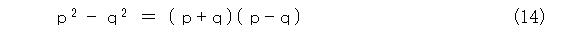
　とりあえず x の関わる項をひとまとめにして２乗の項を作ると式（１５）のようになります。

　

　

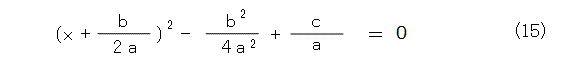
　これをもうちょい変形したものが式（１６）です。ここまでの変形は四則演算しか使っていません。ということは、複素数でも明らかに成り立ちますね。

　

　

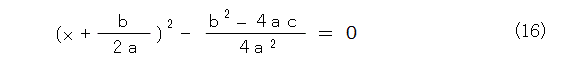
　ここで、式（１４）を使うには、式（１６）の後ろの項がなんかの２乗になればよいわけです。そこで、式（１６）の後ろの項を式（１７）のようになっているとすれば、式（１４）が適用できて、２次方程式の解の公式が得られます。

　

　

　このときに、問題になるのは分子の部分です。否応なく根号が出てきます。ということは、複素数の平方根号がうまく定義できているという仮定の元でのみ意味を持ちます。つまり、２次方程式の解の公式は、複素数の平方根号がうまく定義できていれば使えるということになります。

　

　

４．極形式による表現

　平方根は、２乗の逆のことでしたから、とりあえず、２乗の方を考えてみましょう。２乗は同じものを２回かけることです。そうすると、普通の形の複素数を考えるよりも、極形式で考えた方が、図が描けて見通しがよくなります。

　

　とにかく試してみましょう。複素数を極形式で書くと、式（１８）のようになります。

　

　

　式（１８）を２乗すると、式（１９）になります。

　

　

　図を描くとき、 r はうっとうしいので、無視しましょう。ちなみに、 r を絶対値とか、長さとか、ノルム、 θ を偏角と呼びます。さて、元の複素数と、その２乗を図示すると、図１のようになります。

　

　

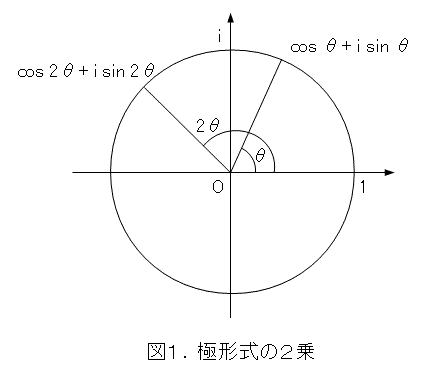
　そうすると、２乗すれば角度が２倍になるので、逆読みして、平方根をとると角度が半分になりますね。

　

　

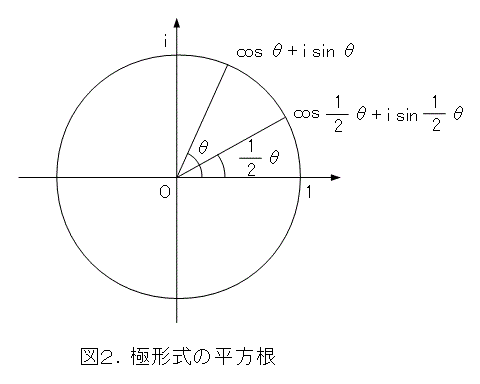
　式で書くと、式（１８）の平方根は式（２０）となります。

　

　

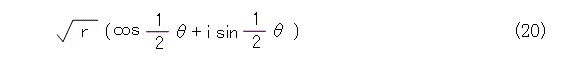
　しかし、三角関数は周期関数でしたから、そのことを考えにいれましょう。式（１８）は式（２１）のように書き直せます。

　

　

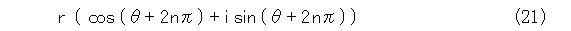
　このときに平方根は、式（２２）のように書けます。

　

　

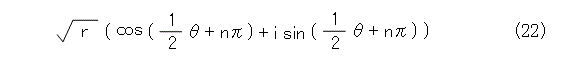
　周期は無視しても差し支えないので、 θ の範囲を、式（２３）のように限定して、式（１８）の平方根は、式（２４）、式（２５）の２個になります。

　

　

　

　

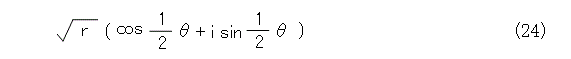
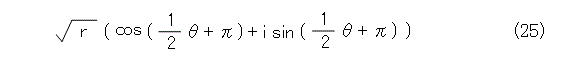
　少し試してみましょう。 i の平方根を考えてみます。このときは、図３に書いてある２個の複素数を２乗すると、本当に i になっていることが、簡単な計算で確かめられます。

　

　

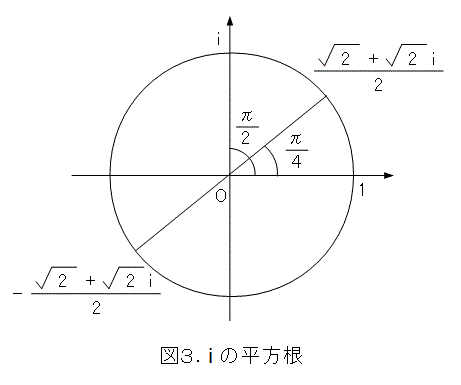
　それでは、式（２４）と式（２５）でどちらを取れば、根号規約が満たされるでしょうか（あるいはどちらもダメかも）。これは、式（２４）、式（２５）がたまたま実数になったときに、根号規約が満たされていることを確かめればよいので、 θ を 0 、 π とおいて、ながめましょう。

　

　こう書くと、ここで破綻する人がいたりします。これ、そのまま数値を代入したのでは、何をやってるかが解かりづらいため、ちょっとした芸当が必要です。まずは、式（１８）を式（２６）のようにおきます。

　

　

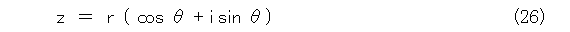
　そうすると、 θ が 0 のとき z は正、 θ が π のとき z は負ですね。このときは式（２７）のようになります。

　

　

　式（２４）と式（２５）とで、 θ を 0 、 π とおいて、式（２７）と合っているのは式（２４）の方です。したがって、複素数の平方根号として取るのは式（２４）です。すなわち、式（２８）です。

　

　

　

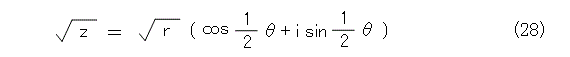
５．複素数の平方根

　極形式を用いると、複素数の平方根は簡単でしたが、「どうしても、複素数の通常の表記じゃなきゃ、ヤダー。」という人がいるかも知れません（本当にいたんだけど）。そういう人には、「じゃ、後は自分で考えてね。よろしく。」と言って放り投げてしまいたいものです。

　

　まあしかし、通常の表記で平方根を考えてみましょう。今度の場合、「力技」でやります。まずは、式（２９）の複素数の平方根を求めます。

　

　

　式（２９）の平方根を式（３０）とおきます。

　

　

　すると、式（３１）が成り立ちます。

　

　

　これから、式（３２）、式（３３）が出てきます。

　

　

　

　式（３２）、式（３３）を解くと、式（３４）、式（３５）が求まります。

　

　

　

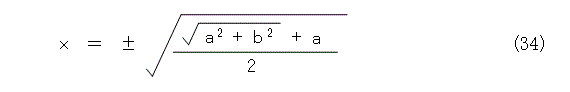
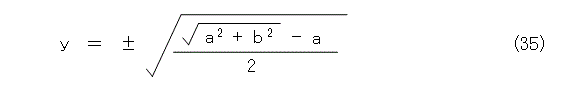
　ここからは、符号の扱いを慎重に行いましょう。 x と y の符号の組み合わせが微妙になります。式（３４）、式（３５）の符号の組み合わせに関係なく、式（３２）が成り立つのは明らかです。

　

　しかし、式（３３）の方は、そう簡単ではありませんね。式（３３）は、 b の符号によって x と y の符号が制約を受けます。 b が正のときは同符号を選び、負のときは異符号を選ばなくてはなりません。

　

　そうすると、式（２９）の平方根は、式（３６）、式（３７）のようになります。

　

　

　

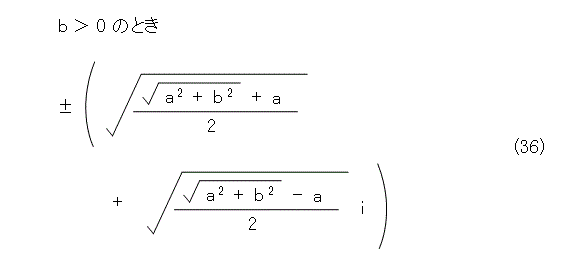
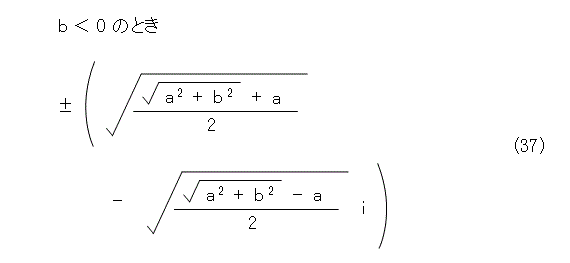
　なんか、とんでもない式になってしまったな。しかも、まだ終わってはいません。根号規約に合っている方を選ぶ考察が必要だからです。その規則に合わせるために、たまたま実数になったときに、実数の根号規約に合っている方を選びます。式（２９）が実数になるのは、 b が 0 のときですね。そうすると、式（３６）、式（３７）のどちらかに b が 0 のときを繰り込んで、根号規約が満たされるかを確かめなければなりません。その上、うまく行く保証はなく、どちらにも繰り込めない可能性もあり得ます（試験問題じゃないもんね）。

　

　b を 0 として、式（３６）の項の中をよくみると、 a が正であれば、第２項が消え、 a が負であれば第１項が消えます。そして、計算するまでもなく、明らかに、式（２９）の平方根は、式（３６）そのものです。つまり、 b が 0 になるときは、式（３６）に繰り込められます。

　

　そうして、＋の方を取ると根号規約を満たすので、平方根号として式（３８）のようにしてよいことになります。

　

　

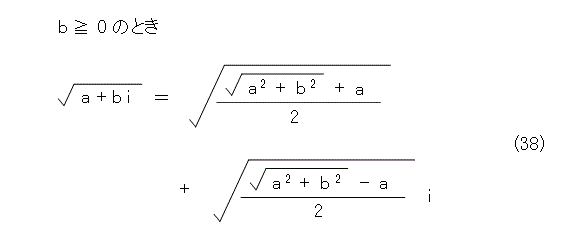
　次に、 b を 0 として、式（３７）の項の中をよくみると、 a が正であれば、第２項が消え、 a が負であれば第１項が消えます。そして、 a が正のときはよいが、 a が負のときは符号が反転します。ということは、平方根号として式（３７）の＋の方と、−の方のどちらを取っても不都合が発生します。つまり、式（３７）に b が 0 になるときを繰り込めません。

　

　そうして、式（３７）は b が 0 になることが排除されてしまうため、式（２９）がたまたま実数になるということを考える必要はありません。それなら、実数の根号規則の適用外ということで、平方根号は勝手に決めてしまってもよくなります。

　

　つまり、平方根号として式（３９）の＋の方と、−の方のどちらを取ってもよいことになりますね。変な気がするかもしれないけど、実数の時には適用できないので、どうでもよいということです。

　

　

　

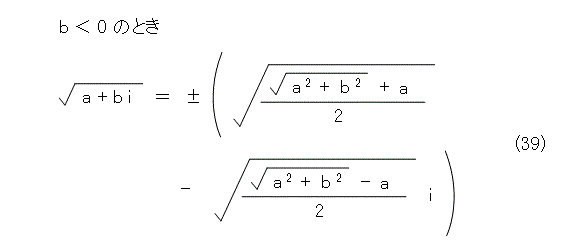
６．おわりに

　今回は、根号について考えました。その中で、やり方、あるいは考え方によっては、わかりやすい結果が出てきたり、ごちゃごちゃであまり使いたくない結果が出てきたりすることをみました。それでも、結果的にはなんとかなりましたが、苦労が徒労に終わる可能性もでていました（ただし、思考訓練にはなる）。

　

　このようなこともあり、一つの考えに固守することは危険を伴います。一つの視点から徹底的に考えることは重要ですが、他の視点から眺めてみることもまた重要です。そうして、いつでもきれいな答えがあるとは思わないことです。答えが出ないことすらあり得ます。この点、本稿を読まれた方はどうお考えでしょうか。

　

完

　

2019年8月11日

著作者　坂田　明治（あきはる）