第１０６話

　パラドックスを楽しもう

　

「主な目的」

今回はパラドックスを楽しむことが目的です。ここで扱うパラドックスは、常識に反した結果が出てくるので、とにかくどこかに間違いがあると当たりがつくでしょう。間違っていると解かれば、あとは、どこが間違っているかを考えるだけです。

　

　

本　文　目　次

　１．はじめに

　２．５千円足りないのは気のせい

　３．１は２に等しい

　４．すべての数は０に等しい

　５．すべての数は互いに等しい

　６．すべての正の数は自分自身より大きい

　７．無限大は０に等しい

　８．人類ハゲ化計画

　９．おわりに

　

著者　坂田　明治

　

　

　

第１０６話　パラドックスを楽しもう

　

１．はじめに

　今回は、パラドックスを楽しんでみましょう。既に、何度かパラドックスについて書いていますよね。にも関わらず、また出てくるのには幾つか理由があります。パラドックスは、一見正しく見える推論の組み合わせから、得体の知れない（常識と矛盾した）結果が出てくることです。とすると、この推論のどこかに誤りがあるということですね。それを指摘することは、よい思考訓練になるからです。（しかし、本当は、結構パラドックスに引っかかる人がいて、面白い笑い話になるからだもんね）

　

　まあ、世の中、苦労して問題を解決しても、何にもならなかったということがよくあります。しかし、パラドックスの解決は、推論の中の誤りを見出して修正することで、これは、以後の教訓となります。丁度、一度敵の罠にかかって危機に陥ったヒーローが、猛特訓の末に復活して、「二度と同じ手は食わぬ。」という台詞を吐いているみたいで、カッコいいですよね。

　

　本稿では、解説をつけません、自分で考えて解決しましょう。

　

　

２．５千円足りないのは気のせい

　昔々、あるところにヲタクがおりました。このヲタク、自作パソコンを作っておったそうな。それで、筐体、電源、マザーボード、CPU、メモリー、ドライブなどを買い集めて作るのだと（コネクターをつなぐだけ）。

　

　これ、おかしくないか。こんなの買い集めて、つなぐだけで、なんで自作パソコンというのだ。ボードから起こすとか、あるいは、どっかから回路図を手に入れて、その回路図に基づいてボードを作るのが自作じゃないのか。

　

　大いに不満だけど、それはともかく、このヲタクは自作パソコンを作っていて、色々買い集めてつなぎました。あと残っている問題はメモリーだけです。メモリーは永久保障、１週間以内返品OKというものにします。もちろん、メーカーは永久保障なんて言ってるだけで、実は、すぐに、次の世代のボードが出て、そのメモリーは使われなくなり、大して保障する必要もないと見込んでいます。

　

　まあ、ともかく、このヲタク、メモリーを買いに店に行き、税込み５千円のメモリーを搭載しようか、税込み１万円で倍の容量のメモリーにしようかと迷いました。さんざん迷ったあげく、５千円のメモリーを買って帰りました。

　

　

　しかし、「安物買いの銭失い。」の格言通り、つまらぬことでケチって、安い方を買うと後悔します。なんだかんだで、やっぱり１万円のメモリーが欲しくてたまらなくなりました。

　

　そして次の日、メモリーを買った店を訪れ、「やっぱり、１万円のメモリーにする。と言って、５千円のメモリーを店に返しました。

　

　

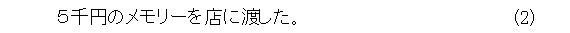
　ヲタクは、税込み１万円のメモリーを受け取って、店を出ようとすると、あわてた店員が、「あのー、差額の５千円を払っていただきたいのですが。」と言いました。すると、オタクは、「何言ってんだ、式（１）と式（２）を見てみろ。昨日、５千円払って、今日５千円のメモリーを渡したんだから、合計で１万円渡したことになるじゃないか。お前は、小学生の算数もできないのか。」と怒り出したそうな。

　

　

３．１は２に等しい

　まず、式（３）が成り立ちます。

　

　

すると、両辺に 9 / 4 を加えて、式（４）が成り立ちますね。

　

　

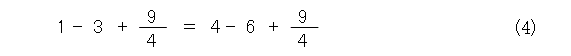
これを平方化して書くと式（５）となります。

　

　

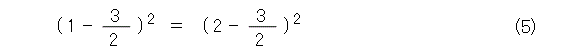
平方根をとって、式（６）が出てきます。

　

　

両辺に 3 / 2 を加えると、式（７）が出てきますね。

　

　

　これで、１は２に等しいことが示せました。

　

　

４．すべての数は０に等しい

　任意に、二つの等しい数、 a と b をとりましょう。当然、式（８）が成り立ちますね。

　

　

あとは、順次、式変形をしていきます。まず、式（９）が成り立ちます。

　

　

すると、式（１０）が成り立ちますね。

　

　

因数分解して、式（１１）が出てきます。

　

　

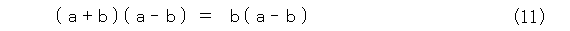
これから、式（１２）が成り立ちます。

　

　

両辺から、 b を引いて式（１３）が出てきました。

　

　

　ほーら、すべての数は０に等しくなりました。

　

　

５．すべての数は互いに等しい

　まずは、任意に、 a と b をとって、その差を c としましょう。つまり、式（１４）です。

　

　

両辺に a - b をかけましょう。式（１５）のようになります。

　

　

展開して式（１６）です。

　

　

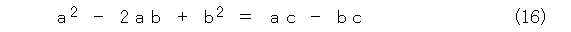
左右の項を少し移項して、式（１７）のようにします。

　

　

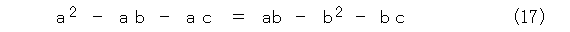
因数分解して、式（１８）のようにします。

　

　

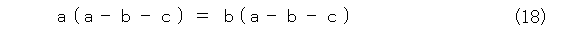
これから、式（１９）がでます。

　

　

　ほーら、すべての数は互いに等しくなりました。

　

　えっ、なんか怪しい気がするって。そういうときは別のやり方でやってみて確かめるのがよいでしょう。色々なやり方でやって、結果が同じなら、確信を持てるようになるはずです。（もっとも、やり方を変えても結果が同じになるという保障はありません）

　

　今度は、任意に、 a と b をとって、その平均を c としましょう。つまり、式（２０）です。

　

　

分母を払って、式（２１）のようにします。

　

　

両辺に a - b をかけましょう。式（２２）のようになります。

　

　

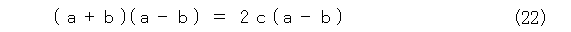
展開して、式（２３）となります。

　

　

左右の項を少し移項して、式（２４）のようにします。

　

　

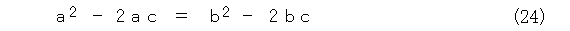
両辺にちょっと項を加えて、式（２５）のようにします。

　

　

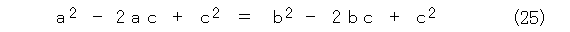
因数分解して、式（２６）となります。

　

　

これから、式（２７）が出ます。

　

　

ほーら、式（２８）が出ました。

　

　

　やっぱり、やり方を変えても、すべての数は互いに等しくなりました。よかったね。

　

　

６．すべての正の数は自分自身より大きい

　今、任意に二つの正の数 a と b を取り、 a の方が b より大きいとします。つまり、式（２９）です。

　

　

両辺に b をかけると（３０）式になります。

　

　

両辺からちょっと項を引いて、式（３１）のようにします。

　

　

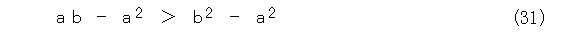
因数分解すると、式（３２）です。

　

　

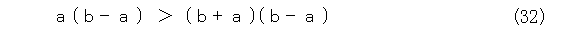
従って、式（３３）がでます。

　

　

ところで、b は正の数だから、同じ数に b を加えると、加えた方が大きくなります。つまり、式（３４）です。

　

　

式（３３）と式（３４）から、式（３５）が成り立ちますね。

　

　

　ほーら、すべての正の数は自分自身より大くなりました。

　

　

７．無限大は０に等しい

　この話は実話が元です。実際、第９５話で出てきたインケンゼミで、「う」が「パシリ君」にやられたことが元ネタがになっています。

　

パシリ君「式（３６）を計算してみろ。」

　

　

う「こんなの簡単ですよ。」

　

　

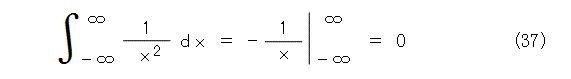
う「ほら、 0 です。」

　

パシリ君「ちょっと関数のグラフを書いてみてくれ。」

　

う「そんなの簡単ですよ。」

　

　

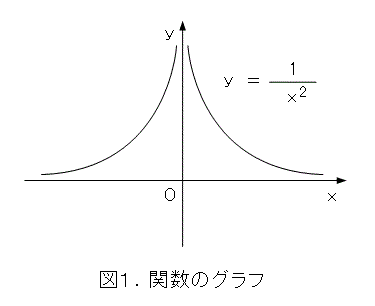
パシリ君「このグラフを見て、なんか気がつかないか。」

　

。。。。。

　

パシリ君「まあ、いいや。この関数は偶関数だろ。」

　

う「そうそう、そう言うと思ってましたよ。偶関数だということを使うと、こうやって計算できますよね。」

　

　

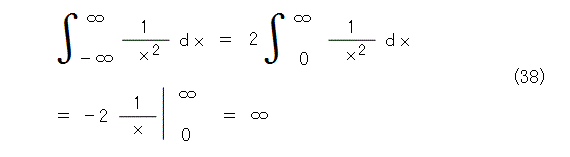
パシリ君「おい、式（３７）と式（３８）とから、式（３９）が出てくるぞ。無限大は０に等しいのか。」

　

　

う「えっ。。。」

　

　まあ、理科好きこども広場ではここまでですが、この後、「う」は「パシリ君」から、この現象をちゃんと説明しろとお仕置きを受けました。後日、「う」がアダマールの有限部分がどうとか説明しても、「パシリ君」は納得せず、インケンゼミで、１変数の超関数（一般化関数ということもある）の勉強会をさせられました。当然、「あ」と「い」は巻き込まれていい迷惑でした。

　

　

８．人類ハゲ化計画

　ある悪の組織での話です。いかに悪の組織の首領といえども、寄る年波には勝てず、だいぶ頭が薄くなってきました。

　

首領「ううっ、髪がかなり薄くなってきた。このままでは、カッコ悪くて、

　　　　スーパーで、かわいいねーちゃんのいるレジに並べないではないか。」

　

　そんなことよりも、買い物カゴに、賞味期限間近で半額になったものばかり入れている方がカッコ悪いと思うぞ（もっとも、こんなおっさん気にもしていないか）。

　

首領「そうだ、人類を全部ハゲにしてしまえばいいんだ。これだ。」

　

　こうして、この悪の組織による「人類ハゲ化計画」が進められました。

　

　でどうしたかというと、以下の通りです。ちなみに、ここでは、 0 も自然数とします。

　

　

　

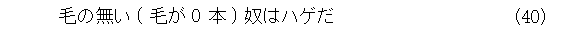
　よって、数学的帰納法により、全ての人類はハゲであると証明された。

　

　こうして、悪の組織の首領のスケベ心によって人類は全員ハゲにされてしまったのである。

　

　ついでに、「ハゲ」の代わりに、「ビンボー」にして、「毛」の代わりに「お金」とすれば、全ての人類が「ビンボー」になるとの証明ができます。他にも、色々使えるので、後は自分で考えましょう。

　

　

９．おわりに

　パラドックスを楽しんでいただけたでしょうか。今回は、簡単なものばかりなので、すぐに誤りが見つかったと思います。

　

　このようなパラドックスでは、得体の知れない結果が出てくるため、どこかで推論に誤りがあると解かります。しかし、実際には、結果があまりおかしくなかったり、それどころか、期待した結果だったりして、推論の誤りに気づかないことがあります。そうして、他人にそれを指摘されたときには、背筋が凍ります。そうならないためにも、せめて、パラドックスで出てくる推論の誤りは念頭に置き、二度と同じ間違いを冒さないように心がけたいものです。この点、本稿を読まれた方はどうお考えでしょうか。

　

完

　

2019年11月29日

著作者　坂田　明治（あきはる）