第１０７話

　連分数を楽しもう

　

「主な目的」

今回は連分数を楽しむことが目的です。連分数表示をすると、平方根などの２次の無理数がきれいな形で表現されます。連分数はディオファンタス解析等で重要な役割を果たしますが、本稿では、無理数の近似という観点で扱っています。まあ、あまり連分数の意味などに拘らず、表現の美しさを楽しんでもらいたいものです。

　

　

本　文　目　次

　１．はじめに

　２．平方根２の近似

　３．連分数

　４．一次変換

　５．近似の精度

　６．循環連分数

　７．おわりに

　

著者　坂田　明治

　

　

　

第１０７話　連分数を楽しもう

　

１．はじめに

　今回は、連分数による近似の仕方です。ユークリッドの互除法とも関連するので、興味のある方は第１８話を参考にされるとよろしいかと。

　

　そう言えば、最近、手で近似するなんていうことはやってないな。大体、電卓が出てきてから、ろくに計算もしなくなったし、数表も見なくなった。こんな状態で、近似のことを書くのか。まあ、いいや。

　

　（ここは偉そうに）どんな実数でも、その近くに必ず有理数がいます。これは望むだけの精度で近い有理数が取れるということです。この性質を、有理数は実数の中で稠密だと言います。

　

　例えば、平方根２を考えてみましょう。

　

　

　式（１）は平方根２を右辺の有理数で近似しています。これに限らず、無理数の小数展開は、有理数での近似の例です。なお、有理数は、自分自身が有理数なので、望むだけの精度どころかドンピシャな有理数が取れています。

　

　さて、平方根２の小数表示はあまりきれいではありませんね（数字の並び方が汚い）。この変な表示を「ひとよひとよにひとみごろ」と覚えさせられて頭にきた人も多いかと（俺）。そこで、もっときれいな表示になる連分数表示を扱おうと思います。

　

　

２．平方根２の近似

　平方根２の近似値を求めましょう。

　

　そう言うと、最初に思いつくのは開平算ですね。やろうと思ったら、一瞬で面倒になって、こんなの電卓で計算すればいいやと挫折しました。書くのも面倒なので省略。なんて話はよくあることです（俺）。

　

　というわけで、ちょいと考えを変えて計算してみましょう。

　

　

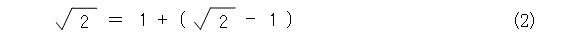
　平方根２の整数部分は１です。そこで、式（２）のように整数部分と小数部分に分けます。

　

　

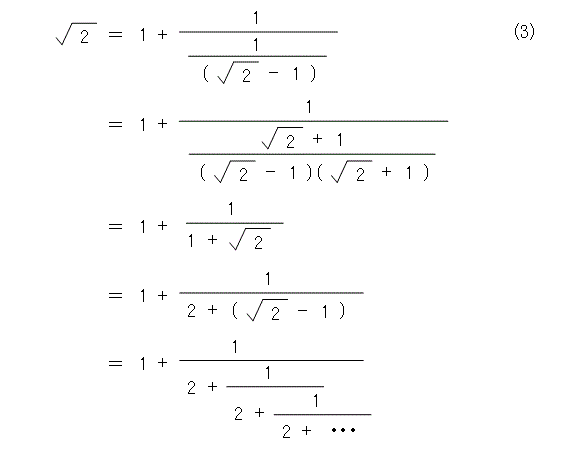
　次に、小数部分の処理ですが、小数の逆数を取れば１より大きくなるので、式（３）の第一式のように分子で分母分子を割ります。そして、第二式のように、整数部分を引き出すために分母を有理化します。その結果が第三式です。整数部分を引き出したのが第四式です。以下、同じことを繰り返して、第五式のようになりますね。

　

　ほーら、きれいな分数の形になりました。調子に乗って、平方根３とか平方根５などの計算をお勧めします。

　

　そうそう、近似計算ですが、式（３）の五式を頭から順番にとって、式（４）のように数列化します（近似値の列）。そして、電卓で計算すると（やっぱり手で計算してない）、割とよい近似になっていることが確かめられます。

　

　

　

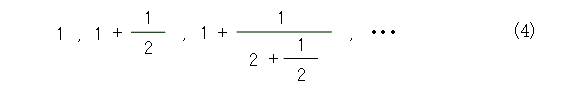
３．連分数

　ここから先、特に断りのない限り、文字は全て正の整数（１以上の整数）とします。更に、文字の説明は一々しません（自分で考えること）。

　

　まず、有理数の場合から考えましょう。第１８話第２章の終わりの方に、ユークリッドの互除法を使って、３３８と７１５の最大公約数を求めているところがあります。それを使って、７１５／３３８を変形してみましょう。

　

　

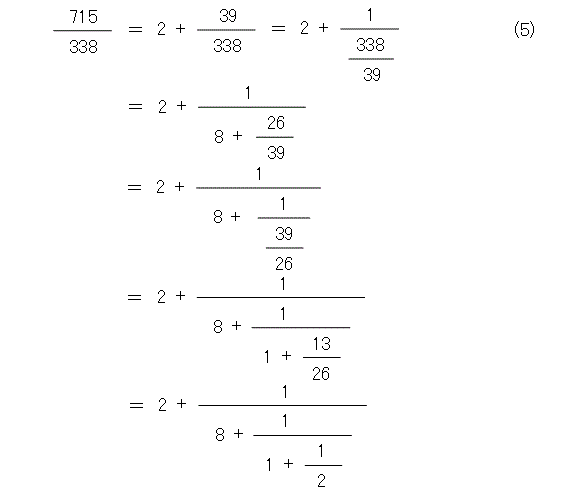
　式（５）のようになって、意外とすっきりした形になります。

　

　次に、上でやったことを、１より大きな正の実数について拡張しましょう。

　

　そのために、式（５）のやり方をよく見てみましょう。基本になるのは、ある数があったときに、その数を越えない最大の整数を引きずり出しているところです。感の鋭い人は気づいたと思いますが、ガウスの記号そのものですね。

　

　一応、定義を書いておくと、実数 x に対して、 x を越えない最大の整数を [ x ] と書きます。

　

　たとえば、

　　[ 1.2 ] = 1

　　[ 2 ] = 2

　　[ 3.14 ] = 3

　　[ - 3.45 ] = - 4

などです。

　

　さて、 x を１より大きな正の実数（特に無理数）とします。すると、この上でやったことと、第２章でやったこととから、式（６）のようにおくのは妥当でしょう。

　

　

小数部分は x - [ x ] です。そこで、

　

　

とおきます。すると、

　

　

のようになります。

　

　更に、式（９）、式（１０）のようにおきます。

　

　

　

　そうすると、式（１１）のようになります。

　

　

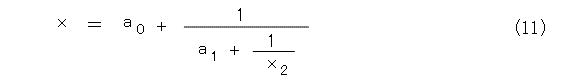
　これで見通しが立ってきましたね。式（１２）、式（１３）のようにおけば、式（１４）のようになります。

　

　

　

　

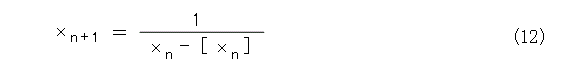
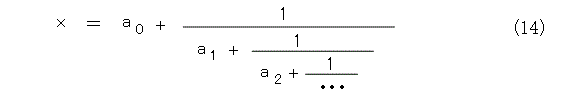
　これから、実数 x は、以下の数列で近似できることが解かります。

　

　

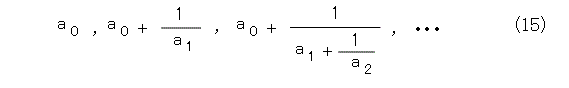
　この、式（１５）の各項を連分数と呼びます。もちろん、式（１４）の右辺も連分数です。特に、第２章で出てきた式（３）の第五式や、式（５）の最後の部分も連分数です。

　

　なお、式（５）から、有理数のときは有限で切れると予想がつくでしょう。この予想が正しいかどうかは自分で確かめましょう。

　

　

４．一次変換

　さて、連分数による近似を考えるのあれば、当然近似の精度評価が問題になります。近似の精度を扱ったことのある人なら知っていると思いますが、よく、ぐっちょんぐっちょんどろどろの計算になります。

　

　なるべくそういうことは避けたいですね。それで、まず最初に頭に浮かぶことは、「もう、ダメだー。」と叫んで諦めることです。そう、そう、さっさと諦めちゃいなさいね（著者一押し!）。

　

　で、ここで諦めないで精度評価をしようとすると、見通しのよい計算方法を考えなければなりません。では、どうしましょうか。

　

　式（１５）をよく見ると、分数式が積み重なっていく形になっています。積み立てられる部分の分数を考えてみましょう。式（８）、式（１１）を眺めてみると、作り方から、式（１６）が出てきます。

　

　

　分母分子を整理して、式（１７）のようになります。

　

　

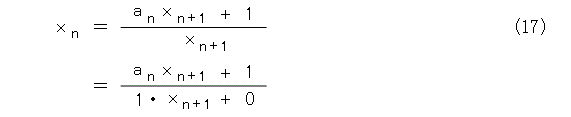
　式（１７）をよくみると、 x_n+1 から x_n への分数変換と考えられます。なんか、いつもと逆向きの変換ですね。

　

　式（１７）をもっと一般的な形にすると、式（１８）のようになります。

　

　

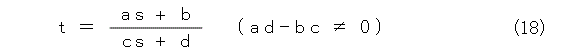
　式（１８）を一次変換と呼びます。これ、第９５話を読んだ人なら、「射影変換じゃないの。」と思うかも知れません。試しに、式（１９）、式（２０）のようにおくと、

　

　

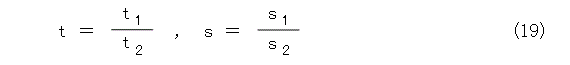
丁度、式（１８）が出てきます。しかも、都合のよいことに、式（２１）の形に書けます。

　

　

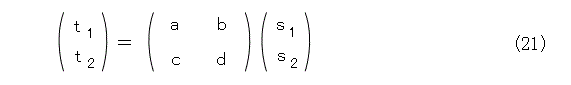
　これから、２つの変換を合成したものは行列の積として計算できますね。しかも、連分数に関する変換は、式（１７）から、逆三角行列です。つまり、変換行列は式（２２）です。

　

　

　こうなってくると、俄然やる気が出てきましたね。

　

　まず、記法を簡略化しましょう。とりあえず、式（２３）のようにおきます。

　

　

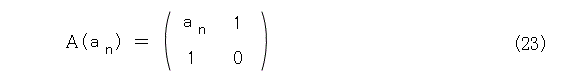
　更に、分数式を無理矢理行列で表します。つまり、式（２４）の記法を導入します。

　

　

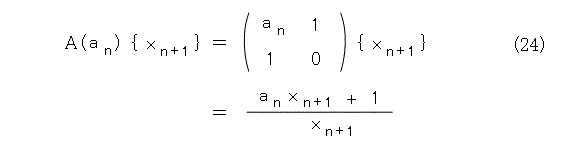
　このようにすると、式（１７）は式（２５）のように書けます。

　

　

　すると、

　

　

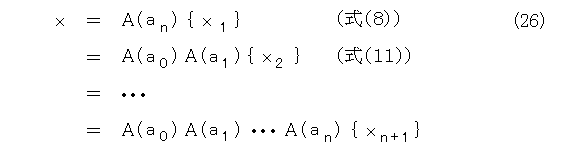
のようになります。きれいな形になりましたね。

　

　しかも、各々の行列は逆三角行列です。逆三角行列の積が計算できれば、近似の精度評価も夢ではありません。

　

　

５．近似の精度

　近似の精度を評価するのに当たって、ぐっちょんぐっちょんどろどろの計算を避けるため、かなり荒い方法を取ります。厳密にやりたい方や、まじめにやりたい方は、あえて、ぐっちょんぐっちょんどろどろの計算をするか、ここでの手法を精密化するか、または、別のやり方を考えてみましょう。

　

　連分数列による近似をするということは、式（２７）から式（２８）を作ることです。

　

　

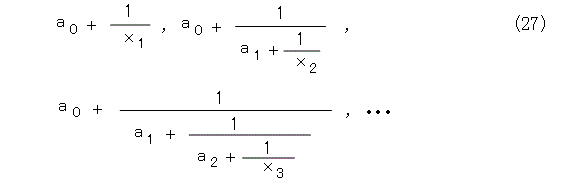
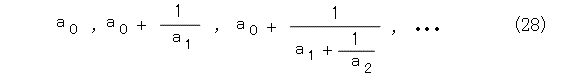
　これは、 x₁ , x₂ , x₃ , ・・・ を全部無限大に飛ばしてしまえば、式（２７）から式（２８）が出てきます。

　

　

　以下では、この方法を元にします。

　

　それでは、式（２６）の行列の積を計算してみましょう。とは言っても、逆三角行列の積は、対角行列の積や、三角行列の積ほど簡単ではありません。計算できるところまで計算して、後はなんか方法を考えることにしましょう。

　

　計算に当たって、こういうときは、n 項までできたとして、 n + 1 項を考えることから始めます。うまく関係式ができないときは、考え直しましょう。

　

　まずは、式（３０）のようにおきます。

　

　

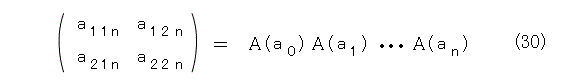
　すると、次の項は式（３１）のようになります。

　

　

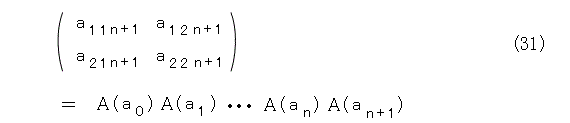
　式（３０）を式（３１）へ代入して計算すると、

　

　

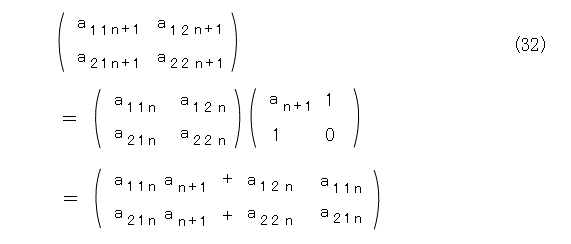
となります。

　

　こういうときは、簡単な方を比較して、複雑な方をそれで表すとうまく行くことがあります。失敗したら、また考え直せばよいので、ここでもそうしてみましょう。第２列を比較して式（３３）が得られます。

　

　

　サヒックスがやたらと付いて面倒なので、あらためて、式（３４）のようにおきましょう。

　

　

　これ、よく見ると、 n を n + 1 とおけば、式（３２）の最初の行列の第１列ですね。そうすると、式（３５）が得られます。

　

　

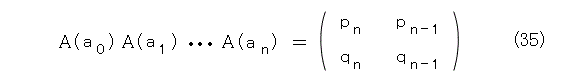
　そこで、 { x_n+1 } を作用させると式（３６）となります。

　

　

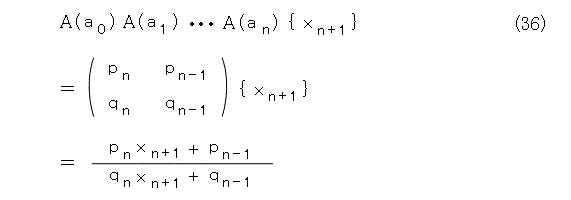
　最初に書いた荒い方法をここでも適用して、 x_n+1 を無限大に飛ばして、式（３７）を得ます。

　

　

　これが、近似する連分数です。

　

　初項から少し計算して確かめてみましょう。（こういう風に書くときは、自信のないときなんだな）

　

　初項は n を０とおいたものですね。

　

　

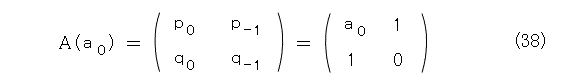
　おおっと、いい加減にやるとこういう問題も起きます。ここは、笑って、「精度評価で、サヒックスが負のものは関係ないから気にしない。」とごまかしましょう（この式で、サヒックスが −1 の場合を定義すると言ってごまかす手もあるが）。

　

　まあ、とにかく、

　

　

となります。確かに、連分数列の初項が出てきました。

　

　

　今度は第２項を計算しましょう。まず、式（４１）です。

　

　

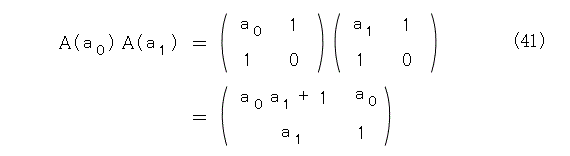
　ここからから、式（４２）を取り出します。

　

　

　すると、式（４３）が成り立ちますね。ここから先の項の計算は自分で確かめましょう。

　

　

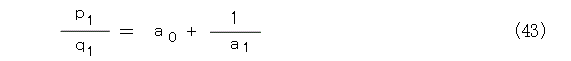
　ここまでくると、近似する連分数が解かったので、あとは、

　

　

を評価するだけですね（誤差の絶対値）。

　

　ところで、式（４５）が成り立ちます。

　

　

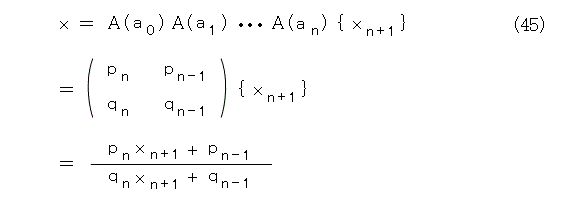
　式（４５）を式（４４）へ代入して計算します。

　

　

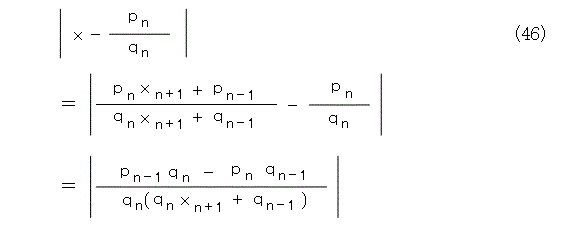
　さあ、困ったぞ。ここからどうしようか。と悩んだら、式を最初からよく見直すことです。なにか使えるものがあるかも知れません。

　

　よく見直すと、式（１８）のかっこの中の部分は全然調べてもいません。これを調べてみましょう。まず、式（１８）のかっこの中は２次行列の行列式が０でないということです。それならばと、他の式をよく見ると、式（３５）が行列式の計算しやすい式になっていることに気づきます。

　

　式（３５）で左辺の行列の行列式は各々の行列（逆三角行列）の行列式の積ですから、−１の n + 1 乗になりますね。右辺については、式（４７）です。

　

　

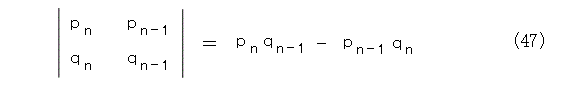
　これから、式（４６）の分子は１です（絶対値を取っているもんね）。分母については、 x_n+1 が１より大きいし、 q_n-1 は正なので、結局、評価式（４８）が得られます。

　

　

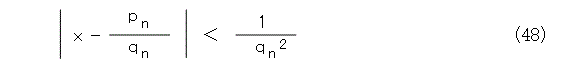
　これで評価式が得られました。式（４８）を見ると、連分数近似は、なかなか精度の良さそうな近似ですね。

　

　

６．循環連分数

　循環連分数というのは、簡単に言うと、同じ数字が循環して表れる連分数です。

　

　式（１２）で、連分数展開に使った各 x_n に対して、同じ列が無限に繰り返しているとしましょう。

　

　

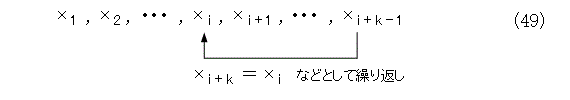
　このとき、式（１４）を作るときに用いた式（１６）から、式（５０）の整数列が得られます。

　

　

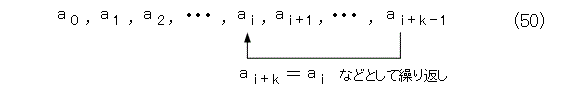
　このように、途中から整数列が無限に繰り返されている連分数を、循環連分数と呼びます。例えば、平方根２の連分数展開がそうです。

　

　そうして、平方根３、平方根５などの無理数を連分数展開して楽しんだ方は、「循環連分数と、２次の無理数とは同じものになるのではないか。」と疑問がわいたことでしょう。なお、２次の無理数というのは、整数係数の２次方程式の解です。２次方程式の解の公式から、式（５１）のような形をしていますね。

　

　

　この予想が当たっているかどうかを調べてみましょう。まずは、循環連分数が２次の無理数になっているかどうかです。

　

　とりあえず、式（４９）が成り立っているとします。そのときに、式（５２）が成り立ちます。

　

　

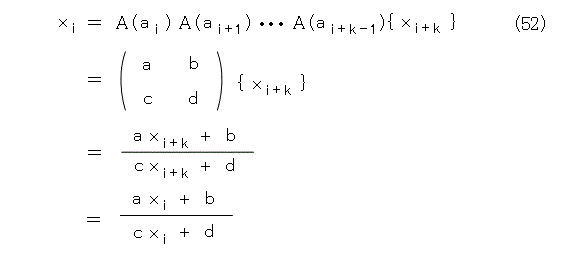
　分母を払って整理すると、式（５３）となります。

　

　

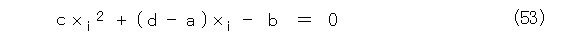
　ところで、式（５４）が成り立ちます。これを x_i について解いて（１次式）、式（５３）へ代入して分母を払い整理すると、整数係数の x の２次式になります。

　

　

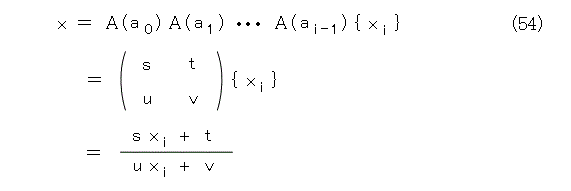
　以上で、循環連分数が２次の無理数になっていることは解かりました。

　

　次に、循環連分数は正のものに限っていることから、正の２次の無理数が循環連分数になっているかどうかを調べましょう。

　

　式（５５）の整数係数２次方程式を考え、これが、正の２次の無理数解を持つとしましょう。

　

　

　この解を連分数に展開したものを式（５６）とします。

　

　

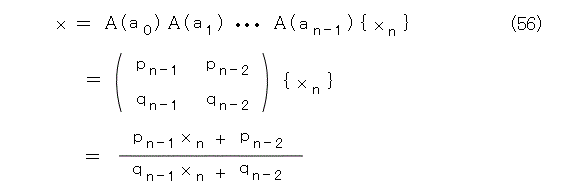
　式（５６）を式（５５）へ代入して、式（５７）を得ます。

　

　

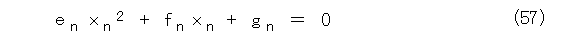
　ただし、２次方程式の各係数は以下の通りです。

　

　

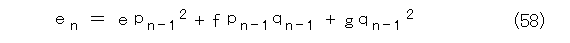
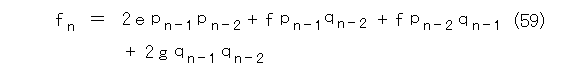
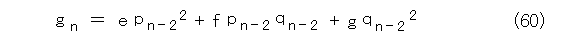
　それで、これからなにをすればよいのでしょうか。やっぱり、「もう、ダメだー。」 と叫んで諦めるしかないのでしょうか。こんなことなら、最初から諦めていた方がよかったかも。。。　←　（だから、最初から諦めるのを一押ししたじゃないか）

　

　でーも、でも、でも、諦めないでやろうとすると、何を示すべきか、方針を考えなければなりません。あえて、それをするなら、まず、式（５７）をよく眺めてみることです。

　

　式（５７）では、 n を動かすと、整数係数の２次方程式は沢山できます。それぞれの方程式の解は２個あるので妥当なほうを並べてみると（この部分手抜きにつき、よく考えてみること）、

　

　

となります。

　

　式（６１）はもちろん無限列ですが、それが循環しているとするなら、出てくる数字は有限個になりますね。しかも、各 x_n の作り方から、一度一致するものが出てくれば、その一致から一致するまでの数字は無限に繰り返されることになります。つまり、循環連分数になります。

　

　とすれば、解が有限個から方程式も有限個、つまり、式（５７）の整係数２次方程式が有限個であるとを示せればよくなります。幸い係数は整数なので、係数の範囲が有限の数で抑えられれば十分ですね。

　

　こう考えてくると、式（５８）、式（５９）、式（６０）のそれぞれが有限の値で抑えられると示せばよくなります。しかも、式（５８）と式（６０）の右辺はサヒックスの違いしかありません。そう考えると、式（５８）と式（６０）の評価だけが問題です。

　

　以下、このことを考えましょう。

　

　式（４８）によって、式（６２）、式（６３）が成り立ちます。

　

　

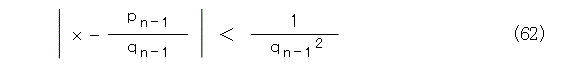
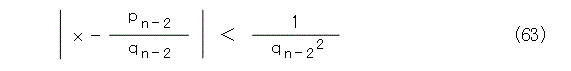
　これから、式（６４）、式（６５）のようにおけます。

　

　

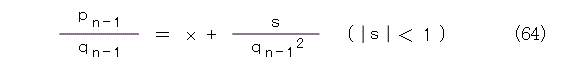
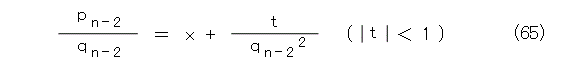
　式（６４）を式（５８）へ代入します。

　

　

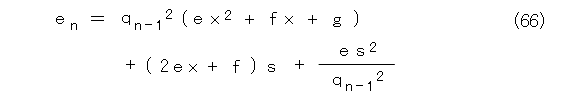
　式（５５）を代入して、式（６７）になります。

　

　

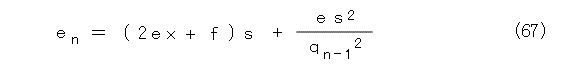
　ここで、 s の絶対値が１より小さいことと、 q_n-1 が正の整数であることを使って、式（６８）が出ます。この式で、 x は式（５５）の解で定数であることから、めでたく、 e_n は有限の値で抑えられることが解かりました。

　

　

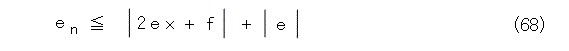
　今度は、式（６４）、式（６５）を式（５９）へ代入します（あまりやりたくない計算だ）。

　

　

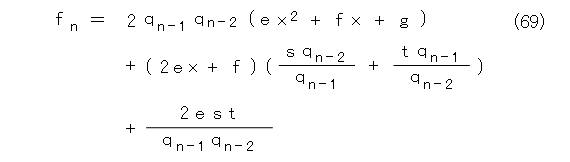
　式（５５）を代入して、式（７０）になります。

　

　

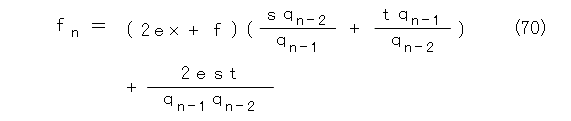
　従って、絶対値を取ると式（７１）のようになります。

　

　

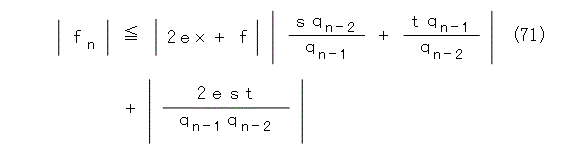
　一方、式（７２）、式（７３）は上で書いたことと同じ理由から成り立つので、問題は式（７４）の評価です。

　

　

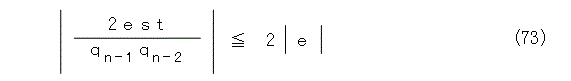
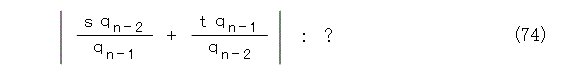
　ところで、式（７４）の評価はどうしましょう。またも行き詰ってしまいましたね。こういうときは、いつもの諦め・・・、ではなく、まず、使える式がないかを見直すことです。

　

　式（４７）は、式（４６）から式（４８）を出すのに使っていますが、式（３５）から行列式が正確に計算できるのに、「絶対値取っているから、どうでもいいや。」と手抜きをしています。何が言いたいかというと、式（４７）は逆三角行列の積だから簡単に出せるのに、式入力が面倒なのでやっていないことです。それを、ちゃんとやると式（７５）です。

　

　

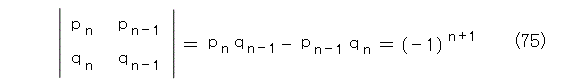
　これから、式（７６）がでます。

　

　

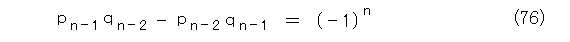
　式（７６）へ、式（６４）、式（６５）の左辺の分母を払って代入します。

　

　

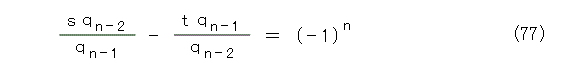
　うーん、惜しいな。もうちょっとなんだけどね。どうにかならないかな。もう一度振り返って、式（４６）の絶対値の中身をちゃんと計算して書くと式（７８）になります。

　

　

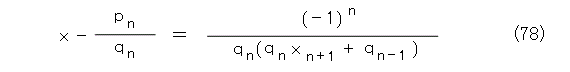
　これを良く見ると、右辺は正になったり負になったりを交互に繰り返しています。つまり、連分数による近似は、大きくなったり、小さくなったりを交互に繰り返して近似していくということですね。だとすれば、式（６４）、式（６５）の s 、 t は必ず異符号になります。そうすると、式（７９）がなりたちます。

　

　

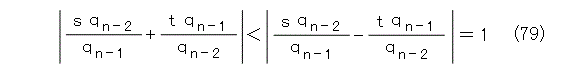
　これで、整係数２次方程式は有限個であると示され、目的は達成されました。めでたし、めでたし。

　

　それにしても、考えもなしにやったり、手抜きしたりすると、後々、跳ね返ってきて、もう一度考え直さねばならなくなるのだね。

　

　

７．おわりに

　今回、考えもなしにやったり、手抜きしたりすると、後で、もう一度考え直さねばならないということを経験しました。これは何も悪いことではありません。やったことを振り返ってよく考えるということにつながり重要なことです。

　

　何か新しいことをするときは、最初から全体が見えているわけではないでしょう。そういうとき、解決のための方針を考えることや、方針転換をすることは重要です。これは、一般によく言われているので、聞いたこともあるでしょう。しかし、やってきたことを振り返って、よく考え直してみることも、また重要です。この点、本稿を読まれた方はどうお考えでしょうか。

　

完

　

2020年4月3日

著作者　坂田　明治（あきはる）