|
第108話
階乗計算で遊ぼう
|

「主な目的」
今回は階乗計算で遊びましょう。具体的には階乗の素因数分解と100の階乗の末尾の連続する0の個数を求めることです。遊び感覚で楽しんでみましょう。
本 文 目 次
1.はじめに
3.0の取り扱い
5.おわりに
著者 坂田 明治
第107話 連分数を楽しもう
1.はじめに
今回は、息抜きとして、 n の階乗の素因数分解を考えてみましょう。
n の階乗は n から 1 までの整数を掛け合わせたものです。

もちろん 1 から n までの整数を掛け合わせたとしても同じです。その場の状況により、見やすくなる方を使いましょう。

特に、素因数分解を考えるときは、式(2)の記法の方が見やすくなります。どうも、心理的に、素因数を小さい方から並べた方が馴染み深くなるようです。確かに、素数は無限にあるので、大きい方から並べるのは無理です。それと、素因数分解を手で計算するときに、小さい素数から順に割り算を行っていくのを体で覚えているのかも知れませんね。
例えば、素因数分解するときに、最初は2で割って、2で割って、・・・と割り切れなくなるまで計算して、割り切れなくなったら、商を3で割って、3で割ってと・・・と計算していきます。このやり方を体で覚えているからでしょう。
2.10の階乗の素因数分解
これ、点数を取らせるための問題として、ときどき中間試験や期末試験に出ることがあります。
10の階乗を式(2)の形式で書き下すと式(3)のようになります。
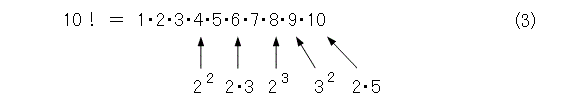
これから、10の階乗の素因数分解は式(4)のようになります。
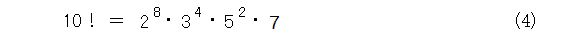
書き下せば簡単に求まるので、点数を取らせるための問題なのですが、これ、10の階乗を実際に計算して、それから第1章の終わりの方で書いたやり方に従って素因数分解する生徒がいるそうです。これ見て、先生の方が悩んでいたとの話でした。
そこで、「そんな、手で計算できるような数にするからそういうことになるのだ。ここはいっそ、100の階乗の末尾にある連続する0の個数を求めさせたらどうだ。」と言う人がいましたが、フルボッコにあったそうです。ちなみに、答えは24個です。後ろの方に回答を乗せますが、ここは自力で算出してみましょうね。
3.0の取り扱い
階乗をやると、最初に引っかかるのが0の階乗です。これを1とするのが約束事になっています。

また、いつもの天下り的な約束事が出てきました。(この約束事が出てくる理由をちゃんと説明する先生はそれなりにいるようなので手抜きしようかな)
まあ、この説明をする前に、0が出てくるとどれだけ痛い目にあうかという実例を示します。毎度出てくるインケンゼミの「パシリ君」と「う」の間で実際にあった話です。これは「う」の入社当事で、まだインケンゼミを結成していません。
「う」が生意気なことを言うので、「パシリ君」が、「ちょっとこれをやってみろ。」と持ちかけたことの一つです。周りに居た人たちは、「あいつら、またやってるよ。」、「また、痛い目にあわされるのに。懲りないな。」と聞き耳を立てていました。ちなみに、パシリ君のいつもの手は中学か高校位の問題に見せかけて仕掛けてきます。確か、小学生位の問題に見せかけたものもあったな。
ここから先、面倒なので、文字の意味は一々書きません。自分で考えましょう。
パシリ君「 m 次式と n 次式とを掛けると何次式になる。」
う「 m + n 次式に決まってるでしょ。」
パシリ君「 n 次式が定数だったらどうなる。」
う「 m 次式に決まってるでしょ。定数は0次式です。」
パシリ君「0は定数だよね。じゃー、0は何次式。」
う「0次式です。」(こんなものも解からんのか。このバカモノめという顔つきでした)
パシリ君「ふーん、じゃー、 m 次式に0を掛けたらどうなる。」
う「そんなの0に決まってるでしょ。あっ。。。」
m 次式に0を掛けたら0ですので、 m 次式にはなりません。これに気づいたようです。
パシリ君「キミの考えている、 m 次式と n 次式を掛け合わせると m + n 次式になるということの基本は、以下の式だろ。」
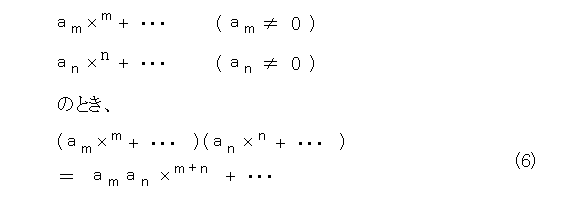
う「そっ、そうですよ。。。」
パシリ君「それで。」
う「式(6)で n を0とすると、定数が0でないときは m + n 次式になります。」
パシリ君「で。」
う「定数が0のときは、慎重に考えなければいけないということですよね。。。」
う「これからは、注意します。」
う「いやー、ためになったなー。。。」
パシリ君「お前、そんな説明で俺が満足するとでも思っているのか。」
う「えっ。。。」
パシリ君「0を別に考えるのはいいとして、 m 次式と n 次式を掛け合わせると m + n 次式になることに例外を作る気か。」
う「。。。」
パシリ君「0の次数を考えて、次数計算が例外なくできるようにする気はないのか。」
う「そっ、そうですよ。そう考えようと思っていたところです。。。」
う「そうすると、0の次数を n として、式(7)が成り立つようにしなければなりません。」

ぱしり君「2次式と1次式と定数の次数は。」
う「そうそう、いやー、そう言われるのを待っていたんですよ。次数の大小から式(8)も成り立たねばいけません。。。」
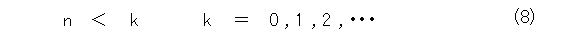
う「でも、こんな数はない。。。」
う「なんて言ってはいけませんよね。。。」
う「うーん、でもこれは。えーと、その、 n はマイナス無限大ですね。そうすると、0の次数をマイナス無限大とすると、ぴったり、 m 次式と n 次式を掛け合わせると m + n 次式になります。」
確かに、0の次数をマイナス無限大とすると、次数の計算が形式的にできて都合よくなります。ちなみに、0の次数を考えないと、式の割り算を行った際に、割り切れたとき、つまり、余りが0で破綻します。余りは割る式より次数が小さくなるということが一般にはいえなくなるからです。この辺は自分で考えましょう。
こういうのを丁寧な説明というんだね。「丁寧な説明」というのは「説明しないこと」というのが巷でささやかれているようですが。
まあ、とにかく。0が出てきたときは慎重に考えなければなりません。そこで、0の階乗を考えてみましょう。(以下手抜き)
そもそも、階乗が出てくるのは、順列・組み合わせのところですね。そして、 n 個のものから r 個のものを取って並べる順列の総数は式(9)のようになります。
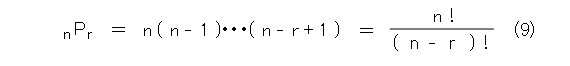
いま、 n 個のものから n 個のものを取って並べる順列の総数は n の階乗通りですから、これを無理矢理式(9)へ代入すると式(10)のようになります。
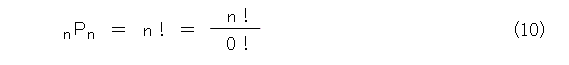
これから、0の階乗は1でなくては機械的な処理ができなくなり不便です。ということで、式(5)を約束事として認める必要が出てきます。そして、機械的計算が滞りなくできるように、n 個のものから0個のものを取る順列も1と定める必要が出てきます。
このようにすると、 n 個のものから r 個のものを取る組み合わせの総数もうまくいきます。ということで、式(5)の約束事は妥当と考えられますね。(やっぱり手抜き)
4.n の階乗の素因数分解
さあ、 n の階乗を素因数分解しましょう。どこから手をつけましょうか。何も思いつかないときは、既に解かっているものをよく眺めてみることです。式(3)と式(4)をよく見てみましょう。
10の階乗を素因数分解すると、1から10までの素数が必ず出てきて、10より大きな素数は出てきませんね。そうすると、 n の階乗の素因数分解では、出てくる素数は1から n までの素数に限られ、しかも、それらは必ず出てくると予想が立ちます。この予想が成り立つことは、 n の階乗の定義から明らかでしょう。
そうなると、それら素数の肩に乗っている指数を求めればよくなります。つまり、式(11)の指数をどうにかして計算するのが目標となります。(1から n までの素数は k 個とする)

そこで指数の計算ですが、これも10の階乗が手がかりになります。2の指数を求めようとすれば、2が何回出てくるかを数えればよいので、式(12)のように書き下します。
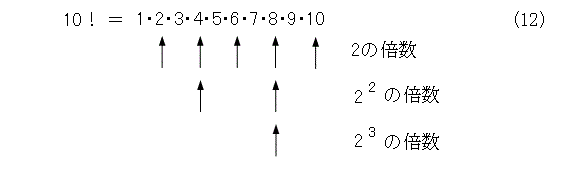
これを見れば、矢印の数が丁度指数の数になり、矢印が連なっているところが、丁度べき乗の数になります。そうすると、1から n までで、2の入ってる個数、22の入ってる個数、23の入ってる個数、・・・を求めてその総和を取ればよいことが解かります。
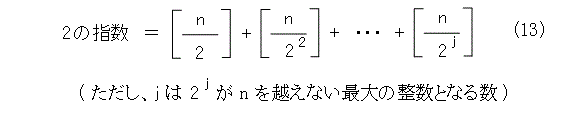
ここで、 [ ] はガウスの記号です。つまり、ある数があったときに、その数を越えない最大の整数のことです。
たとえば、
[ 1.234 ] = 1
などです。
以上から、素数 p の肩に乗っている指数は式(14)のように求まります。
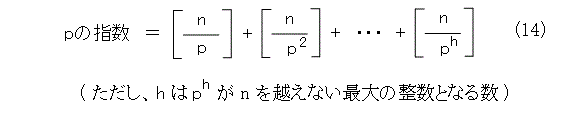
これで、 n の階乗の素因数分解ができました。
ここで、フルボッコにあったという、100の階乗の末尾にある0の個数を求めてみましょう。
まず、10の1乗は0が1個。10の2乗は0が2個。だから、100の階乗の末尾にある0の個数は100の階乗の中に入っている10のなんとか乗の最大値となります。10は2と5の積に分解され、100の階乗の構成から、2の指数は5の指数よりも圧倒的に多くなっています。そうすると、5の指数さえ解かれば、それが10のなんとか乗を表しています。
以上を考えに入れて、式(14)を使うと、式(15)が出てきます。
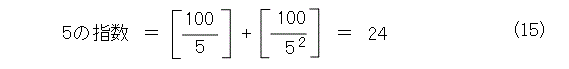
従って、100の階乗の末尾には0が24個連続していることが解かります。
5.おわりに
階乗に関わることは、やたらと数が大きくなり、計算を断念することが多々あります。今回扱った、100の階乗の末尾の0の個数も、いきなり求めさせられたら、どぎまぎしてしまうのかも知れません。これは恐らく、最初に、100の階乗を計算することが頭に浮かぶからでしょう。しかし、階乗の素因数分解は意外と簡単であり、素因数分解を利用して、解決できる問題もそれなりにあります。
何かに直面したとき、最初から、思考停止状態になることなく、常に何らかの手を考えるようにしたいものですね。この点、本稿を読まれた方はどうお考えでしょうか。
完
2020年8月2日
著作者 坂田 明治(あきはる)
|