第１０９話

　オイラーの定理を考えよう

　

「主な目的」

今回は初等幾何について多少なりとも興味のある人が対象です。オイラーの定理を拡張する試みを通して、舗装道路を進むよりも、遠回りして、でこぼこ道を進み、周りの風景を楽しむということを実感する試みです。

　

　

本　文　目　次

　１．はじめに

　２．オイラーの定理

　３．空間への拡張

　４．平面への拡張

　５．おわりに

　

著者　坂田　明治

　

　

　

第１０９話　オイラーの定理を考えよう

　

１．はじめに

　今回は、オイラーの定理について考えましょう。

　

　まず、オイラーは業績が多すぎ、オイラーの名前を関したものも多数あるため、「オイラーの定理」が何のことかわからない人も多いかと思います。ここで、出てくる「オイラーの定理」とは、初等幾何で出てくる定理です（中学で出てきたと思うが）。

　

　実際どういうものかといえば、４点A、B、C、Dが一直線上に、この順序で存在するときに、式（１）が成り立つというものです。

　

　

　

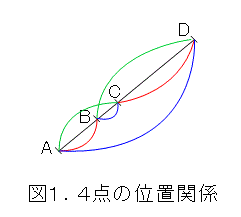
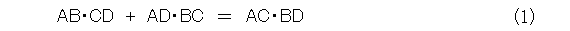
　まあ、この定理に関して、第１０４話でやったみたいな拡張を考えるわけです。はたして、うまく行くかどうか。

　

　

２．オイラーの定理

　さて、オイラーの定理って何に使うのでしょうね（これ、何か使い道あったけかなー）。昔のことなので覚えていません（記憶にありません。など、都合の悪いことをごまかすときによく使う言い方）。

　

　「こんな、得体の知れない定理の拡張を考えて何か出てくるのか。」と思う人も多いと思います。そもそも、拡張なんてできるのか、得体の知れないものを拡張しても、益々何がなんだかわからなくなるだけだと思うのが、普通の考え方でしょう。

　

　理科好き子供の広場では、失敗することも許されているので、何だかわからないものを拡張しようとして失敗し、結局、何も得られなかったとしても問題ありません。つまり、「最後まで読んだのに何も得られなかったじゃないか。時間の無駄だ。」となっても、「知らんもんねー。」で済ませてもよいということです（これ、テレビの番組でよくあるけど）。

　

　まっ、ともかく、やってみようじゃない。

　

　と言うことで、この章では、オイラーの定理が成り立つ理由を示します。

　

　まず、４点A、B、C、Dが一直線上に、この順序で存在するということから、図２のように座標を導入します。

　

　

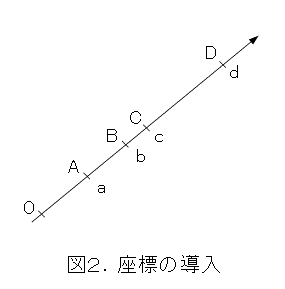
　すると、式（２）のように各線分の長さが計算できますね。

　

　

　後は、式（１）の左辺から右辺を引いたやつをゴリゴリ計算するだけです。

　

　

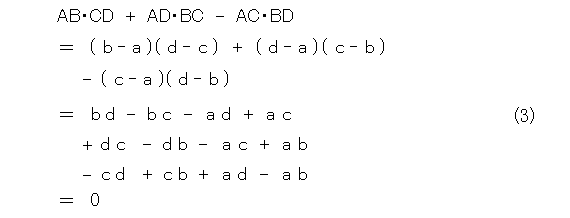
　ほーら、0 になったので、式（１）は成り立ちます。

　

　式（３）を少し書き直すと、式（４）の恒等式が得られます。

　

　

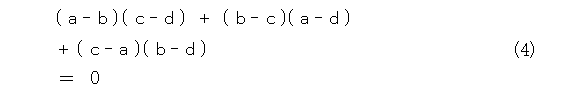
　「なるほど、オイラーの定理の正体はこの恒等式だったのですね。いやー、よくわかった、めでたし、めでたし。」と納得する人はいないと思いますが、どうでしょうか。

　

　

３．空間への拡張

　２点を配置すると、一般的には線分ができ、３点を配置すると、一般的には三角形ができます。そこで４点を配置すると、一般的には、三角錐、つまり、四面体ができます。このとき、オイラーの定理は成り立つでしょうか（いつものように、点が重なっている場合など、一々細かいことは書かないので、自分で考えること）。元々４点の配置だったので、空間への拡張から考える方が自然かも知れませんね。

　

　

　こういうとき、まずは、都合のよさそうな図形を考えてみるものです。例えば、正四面体です。

　

　

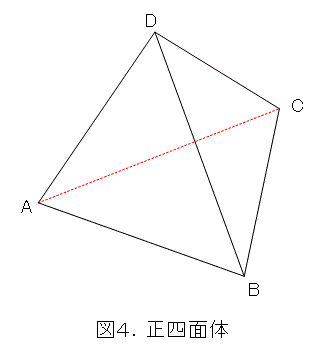
　正四面体の各面は、正三角形ですよね。それで、各辺の長さは全て同じになります。すると、明らかに式（１）は成り立たず、式（５）となります。こんな特殊な、恐らくは、四面体中一番簡単な図形ですら成り立たないなら、これはもうこの先なにも出てこないような気がします。いつものように、「もう、ダメだー。」と叫んで諦めましょう。

　

　

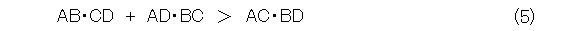
　まっ、それはともかく、なんとかいじくって、無理矢理成果につなげられないかな。

　

　オイラーの定理が、式（４）の恒等式だったことを思い出しましょう。そして、この恒等式に相当するものを作ってみます。

　

　図２に習って、位置ベクトルの原点を導入しましょう。

　

　

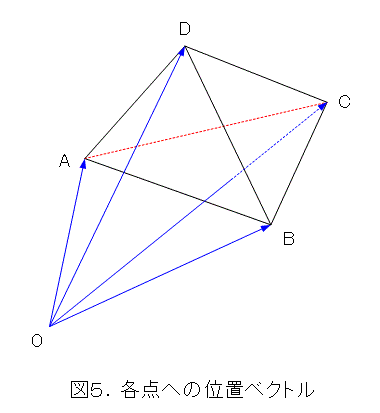
　次に、式（４）の恒等式の項をベクトルとして形式的に書き直します。

　

　

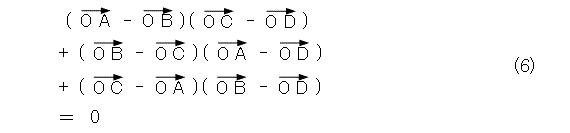
　このベクトルの間の積は、どう考えればよいでしょうか。空間でのベクトルの積は、内積と外積がありますね。最初に外積と考えてみましょう。そうすると、交換律が成り立たないので、式（６）は恒等式になりません。

　

　では、内積と考えてみましょう。このときは、式（６）が成り立ちます。これから、式（７）が出てきます。

　

　

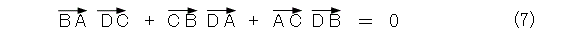
　で、これでなんなの。一般的に成り立っているだけで、その４点の間の位置関係はどうでもよいということです。最初のオイラーの定理では、４点の位置関係を規定したことを思い出しましょう。またもや破綻です。

　

　それでも、ここから何か出てこないでしょうか。破綻しても、無理矢理成果があったことにしてしまうのは、どっかの国の常套手段です。

　

　よく式（７）を見ると、内積が 0 の項が二つあると、残りの一つも 0 でなくてはなりません。内積が 0 とは垂直ということですから、式（７）から、２組の対辺が垂直ならば、残りの１組も垂直となりますね。これは、第１０４話で出てきた直辺四面体になるということです（正四面体も直辺四面体）。

　

　これでいいかな。こんな程度では、この試みは失敗という人も多いでしょう。

　

　

４．平面への拡張

　空間化は失敗したので、今度は平面化してなんとか成果が出ないかを考えてみましょう。

　

　まず、式（１）を直接扱うと失敗しそうなので、恒等式の方から、搦め手（からめて）で迫ってみます。

　

　最初に、式（７）は、特に次元とは関係なく成り立つので（成分を使って計算したものではないから）、平面のベクトルでも成り立ちます。そこで、４点の配置が図６のような場合を考えてみましょう。

　

　

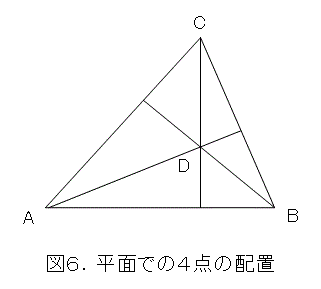
　このときに、２組の対辺が垂直ならば、残りの１組も垂直となることは、式（７）から出てきます。例えば、線分ABと線分CDが垂直、線分BCと線分ADが垂直ならば、線分ACと線分BDも垂直になるということです。つまり、点Dは三角形ABCの垂心です。

　

　なるほど、平面で考えると、面白そうな結果が得られるとの期待を持たせてくれそうですね。

　

　さて、平面上の点は複素数に対応することと、式（４）の恒等式は、四則演算しか用いてないので、当然、複素数でも式（４）は成り立ちます。そこで、各点A、B、C、Dに対応する複素数をそれぞれ、 a 、 b 、 c 、 d としても成り立ちます。

　

　では、ここで何をすればよいのでしょう。式（４）は元々、オイラーの定理である式（１）からでてきました。思い起こすと、各点は直線上の点なので、それぞれに実数を割り当てていました。

　

　平面上では、各点に複素数を割り当てています。複素数は、長さと偏角によって決まりますよね（極形式）。そうすると、複素数で式（４）が成り立つということは、長さと偏角込みで式（４）が成り立つということです。

　

　一方、実数では、原点の取り方によって、長さに正負はあるとしても、式（４）は長さに関する式です（元々、オイラーの定理である式（１）は長さの式）。

　

　そうすると、複素数の式（４）から、長さに関する式を導き、その上で考えるとよさそうですね。

　

　この方針にしたがって、式（１）っぽくなるように変形して式（８）を得ます。

　

　

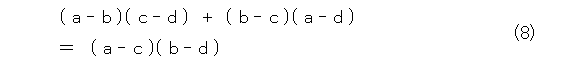
　複素数の絶対値を取ると長さになるので、両辺の絶対値をとりましょう（ここはベクトルでも同じ）。

　

　

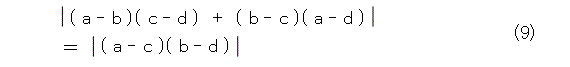
和の絶対値は、絶対値の和で抑えられるので、（この部分はベクトルでも成り立つ）

　

　

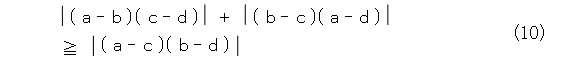
積の絶対値は、絶対値の積に等しいから、式（１１）が出てきます。（内積の絶対値は、絶対値の積以下になるため、この部分がベクトルでは出てこない。つまりベクトルではここで破綻）

　

　

　式（１１）を線分で書き直しましょう。

　

　

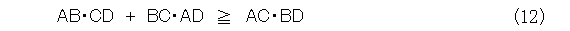
　かなり式（１）似たものが出てきました。違いは不等号がくっついていることです。こう書くと、「何が似ているだ。第３章の最初で、正四面体では不等号になって挫折したじゃないか。等号がちょっと付いているだけで、どういうつもりだ。」と文句が出るかも知れません。その辺の言い訳を少し考えなくてはいけませんね。

　

　平面上で、４点で定まる図形の内、一番簡単な図形は正方形なので、正方形で考えましょう。

　

　

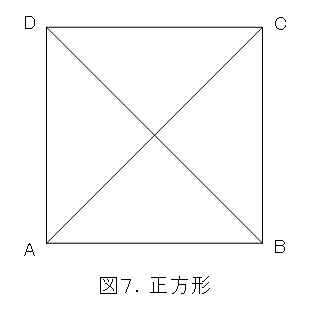
正方形では、各辺の長さは全て等しいので、式（１２）の左辺は、

　

　

となります。一方、対角線は互いに等しいので、式（１２）右辺は、

　

　

となります。そこで、三平方の定理によって、式（１２）の等号が成り立ちます。

　

　つまりオイラーの定理で出てきた式が成り立ちます。ここから、式（１２）で意味のあるのは等号が成り立つときであるとの見当が付きます。そういう目で今までのことを見直すと、式（９）から式（１０）へ行くときに、等号が成り立っている場合が問題だとわかります。

　

　ここで、複素数のことを少し考えましょう。点X、Yを表す複素数をそれぞれ、 x 、 y とします。このときに、式（１５）が成り立つのはどんなときでしょうか。

　

　

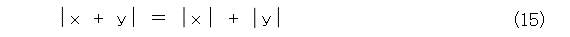
　複素数の和を図示すると、図８のようになります。ただし、図８の右側の図は、同一直線状に乗っているものを少しずらして描いています。

　

　

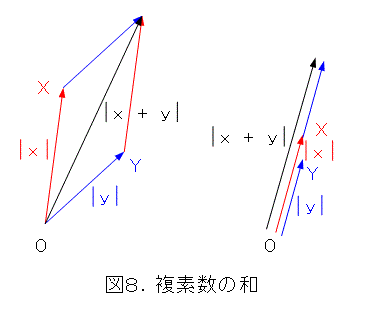
　図8から、式（１５）が成り立つのは、点O、X、Yが同一直線上にあるときだとわかります。しかし、和は、見た瞬間にわかるものではなく、作図しないとどこだかわかりませんね。

　

　試しに、補助的な矢印を消すと図９のようになって、どこだかわからなくなりますよ。

　

　

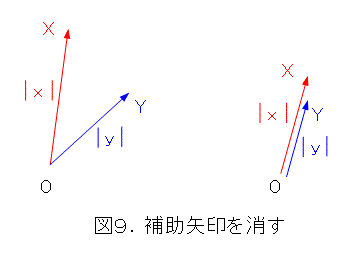
　このまま続けてもできますが、やっぱり図が見やすい方がわかりやすいので、そっちの方を考えてみましょう（このまま続けるのは読者の宿題）。

　

　和の絶対値を取ったから、あまり見やすいとは言えない図になりましたが、どうせ絶対値なんだから和でも差でも大して変わりません。そこで、差の方にしてみましょう。つまり、式（１６）で考えます。

　

　

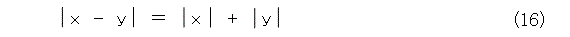
　差の状況は図１０です。わかりやすさが一目瞭然ですね。

　

　

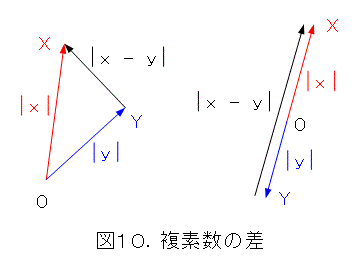
　まあ、気づいている人もいると思いますが、ベクトルを矢印で表したときに、差の作図の方が簡単だったよね。

　

　以上から、式（１６）を使う方向で修正をかけましょう。式（９）を修正した結果が式（１７）です。

　

　

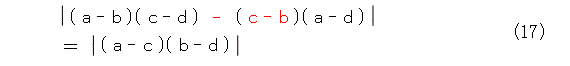
　同様に、式（１０）を修正した結果は式（１８）です。

　

　

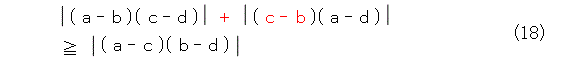
　さて、式（１６）が成り立つのは、図１０の右側の図だから、複素数の偏角が式（１９）のようになります。もちろん、 n は整数です。（以下、この手の注意も書かないので、自分で考えること）

　

　

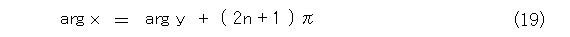
　この事実と、式（１６）と式（１７）とから、式（２０）が出てきます。

　

　

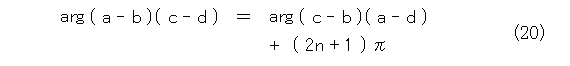
　複素数の積は、長さの積と偏角の和なので偏角に注目して、式（２１）が成り立ちます。

　

　

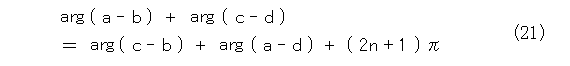
とりあえず、項を移項して、式（２２）のようにします。

　

　

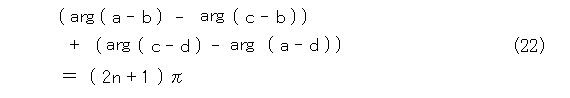
　ここで、複素数の偏角は、図１１のように色々とれます（原点のまわりを何回か回ってもよい）。

　

　

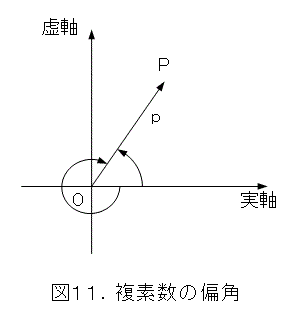
　そこで、以下、角度に正負をつけ都合のよいものを取って扱います。

　

　式（２２）を角度の式に書き直すと式（２３）のようになります（イメージしにくい人は図１２を先に見るといいかも）。

　

　

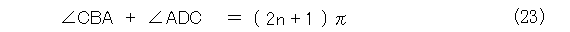
　やりたくない場合分けをしなくてはなりません。まずは、４点A、B、C、Dが反時計回りの四角形をなすとします。つまり、図１２のようになっている場合です。文字の説明を含め、細かいことは説明しません。図を見て自分で考えましょう。

　

　

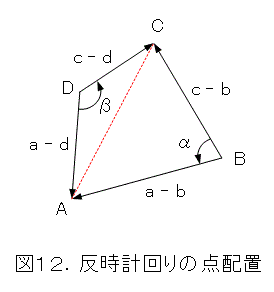
このときは、

　

　

だから、式（２３）から、

　

　

が成り立ちます。

　

　よく知られているように、式（２５）が成り立つならば、四角形ABCDは円に内接します。

　

　今度は４点A、B、C、Dが時計回りの四角形上をなすとします。つまり、図１３のようになっている場合です。

　

　

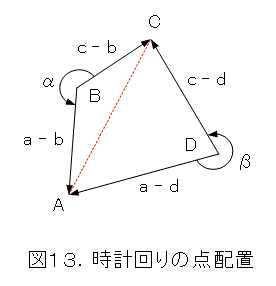
このときは、

　

　

だから、式（２３）から、

　

　

が成り立ちます。これを、四角形の内側の角の関係に変形すると、式（２８）となります。

　

　

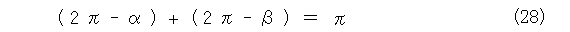
　このときも、式（２８）が成り立つならば、四角形ABCDは円に内接します。

　

　次に、４点の位置関係がねじれている場合を考えます。４点A、B、C、Dが反８の字回りに配置されているとすると図１４のようになります。

　

　

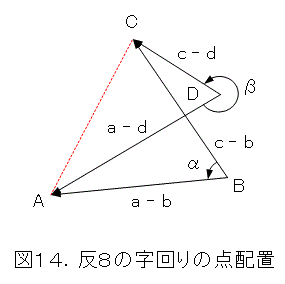
このときは、

　

　

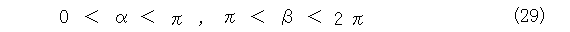
となって、

　

　

だから、式（２３）は成り立ちません。

　

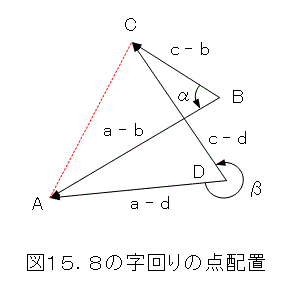
　４点A、B、C、Dが８の字回りに配置されている場合は図１５のようになります。このときも図１４と同様に式（２３）は成り立ちません。

　

　

　以上から、式（２３）が成り立つのは、四角形が円に内接しているときに限ることがわかりました。この部分、つまり、平面上の相異なる４点A、B、C、Dについて式（１２）の等号が成り立つ場合、つまり、式（１）が成り立つときに、４点A、B、C、Dは円に内接する四角形ABCDとなります。これがトレミーの定理です。

　

　でも、この話はまだ終わりません。

　

　じゃー、四角形とならない場合はどうなるのでしょうか。

　

　まず、点Bが直線ACの上にあるとします。ここでは、更に、線分ACの上にあるとしましょう。

　

　

そうすると、

　

　

だから、式（２３）から、

　

　

となりますよね。すると、点Dは直線AC上で線分ACの外になければなりません。

　

　点Bが直線AC上で、線分ACの外であってもほぼ同様です。

　

　したがって、４点A、B、C、Dは直線上にあって、点AとC、点BとDは互いに他を分割します。例えば、 ４点A、B、C、Dが一直線上に、この順序で存在するということです。あれ、これオイラーの定理そのものじゃなかったっけ。なんかお釈迦様の掌の上を飛び回って、結局は元の所へ戻ってきただけじゃないか。

　

　

５．おわりに

　今回、オイラーの定理について考えました。その中で、わざわざ余計な手間をかけて拡張を考えて行きました。具体的には、恒等式との関係を考え、その恒等式に着目して拡張を試みようというやり方です。

　

　通常、わざわざ余計な手間をかけるというのは、裏に何らかの目的があります。簡単な方法や、直接的な方法を避けて、遠回りするというのはよい思考訓練になります。何度か出てきましたが、理科好き子供の広場では、舗装道路を進むよりも、遠回りして、でこぼこ道を進み、周りの風景を楽しむということを推奨しています。この点、本稿を読まれた方はどうお考えでしょうか。

　

完

　

2020年12月27日

著作者　坂田　明治（あきはる）