|
第110話
曲線の接触を考えよう
|

「主な目的」
今回は曲線の接触について多少なりとも興味のある人が対象です。少し微分を使いますが、曲率円を構築する試みを通して、曲率円の図形的イメージを楽しむものです。
本 文 目 次
1.はじめに
2.接線
3.接円
4.曲率円
5.おわりに
著者 坂田 明治
第110話 曲線の接触を考えよう
1.はじめに
今回は、曲線の接触について考えましょう。
よく考えたら、ちょっと難しいな(書くのが)。曲線がうまく描けないもんね。一応、円や楕円は描けるけど、曲線の描画機能は使いにくく面倒。更に、曲線を接続したときに接続点が滑らかにならないよ。実は、今までに描いてきた曲線は、かなりインチキだ。それらしく見せてるだけだった。手書きなら楽なのになー。
まあ、それはともかく、曲線の接触に戻ります。まず、ここでの曲線は自分自身と交わらない滑らかな連続曲線とします。いつものことですが、都合よく扱える状況などを一々細かくは書きません。それらは自分で考えて補いましょう。
2.接線
最初に扱うのは接線です。これ、一番簡単な例は、円の接線でしょう。
とりあえず、円と直線の位置関係を描いてみましょう。
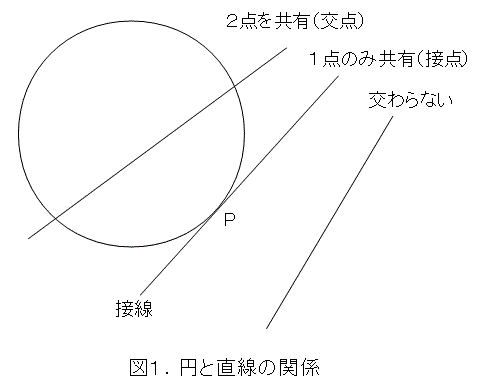
図1のように、直線は2点で交わるか、1点のみ共有するか、全然交わらないかのいずれかですね。そして、1点のみ共有している直線を、円の接線というのでしたね。
これを式で書いてみましょう。円の方程式と直線の方程式は、それぞれ、式(1)、式(2)のようになります。
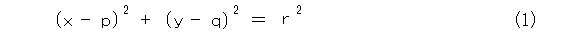

円と直線の共有点は、式(1)と式(2)とを連立させたときの解になります。その解が、1個のみのときに接しています。したがって、式(2)を x か y について解いて、それを式(1)へ代入しできた2次方程式の解が1個のみのときが接線です。2次方程式で解が1個のみというのは、重複解のときに限るので、判別式を使えば接線が求まりますね。
これから、曲線の方程式が n 次式のときには、重複解を持つという条件を使えば接線が求まりそうです。でも、一見これで求まりそうな感じですが、よく考えたら(考えなくても) n 次式の判別式なんて知りません。
それどころか、三角関数や指数関数、対数関数などでは、お手上げです。こうなってくると、いつものことで、さっさと諦めてしまうというのが頭に浮かんできます。
もう一度、円で考えてみましょう。2個交点があるときに、片方の交点をもう一方の交点に近づけていけば、各々の交点を通る直線は接線に近づきます。
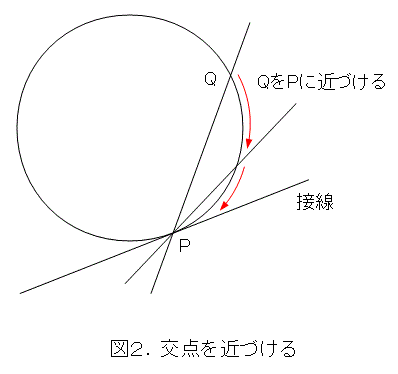
確かに、重複解は、2個の解が重なったもの、つまり2個の交点が重なったものです。そう考えると、片方の交点をもう一方の交点に近づけた極限の姿と考えるのがよさそうです。これなら、判別式を必要とせず、色々な曲線に適用できそうですね。
そこで問題となるのは、片方の交点をもう一方の交点に近づけた極限が一意的に定まる(存在して1個ということ)かどうかです。滑らかな連続曲線なら問題ありません。これを確かめるのは、当然読者の宿題です。
それはそうと、ただ、円は簡単に描けて解りやすいし、図形として扱いやすいのだけれども、式の取り扱いが面倒です。式(1)を、それぞれ y 、 x について解くと、
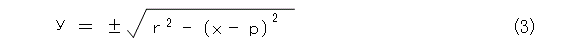
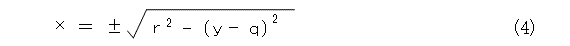
となり、関数として扱うときは少し面倒になります。そもそも、円は、座標軸に平行な接線を持っているため、 y について解いた式でも、 x について解いた式でも破綻する点が出てきます。
そこで、円を図3のように、4つの弧の集合と考えましょう(それぞれ、式(3)、(4)の4つの式に対応している弧)。図では、見やすくするために、各弧をちょっとずらして描いています。
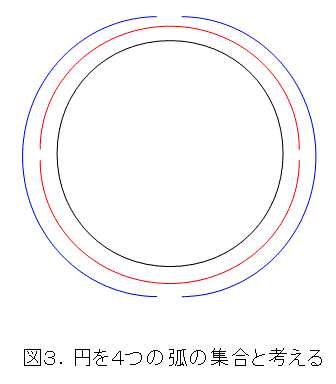
こうしておいて、各接線を求めるときは、都合のよい弧を用いて計算すればよいでしょう。
このように曲線は、一つの式で全体を表現せず、それぞれ都合のよい式で表現できる部分を貼り合わせて考えればよさそうですね。ここでは、これ以上深入りはしません。詳しく知りたい人は自分で考えましょう。
ともかく、代表として、通常の関数表現 y = f(x) で考えておけばなんとかなりそうですね。
さて、 y = f(x) と2点 ( t , f(t) ) 、 ( t + h , f(t + h) ) で交わる直線は図4のようになります。
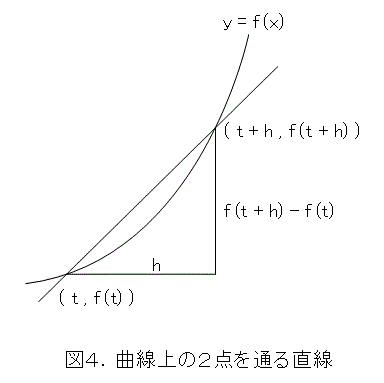
これから、傾きは式(5)となります。
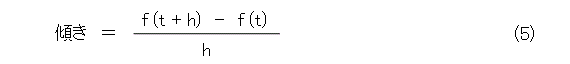
したがって、直線の方程式は式(6)のようになります。
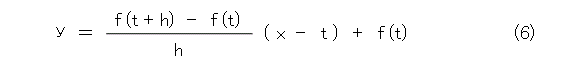
h を 0 に近づけて極限を取れば、接線は式(7)となります。
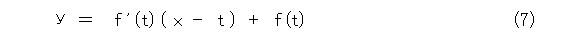
その際に、図4で h を 0 に近づける様子を見れば、接線は曲線を近似していることが解かりますね。
3.接円
次は接円ですが、これ、いきなり破綻していますね。図5を見れば、直線上の点Pで直線に接している円は沢山あり、一意に定まりません。
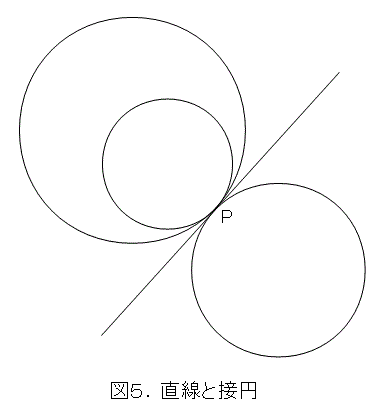
前章のように、曲線上の2点を取って、そこを通る円を描いてみようにも、2点で円は定まらないため、沢山の円が候補にあがってきてしまいます。
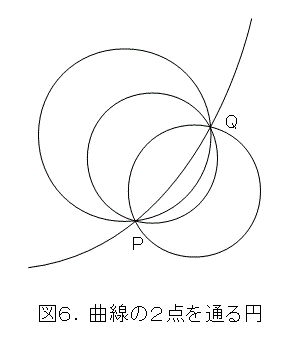
やはり、破綻ですね。もう諦めましょうか。
4.曲率円
円の性質をよく考えなおしてみましょう。円の作図をやった人ならよく知っていると思いますが、一直線上にない3点が与えられると、その3点を通る円は一意に定まります。3点からどうやって円を作図するかは知っていますよね。
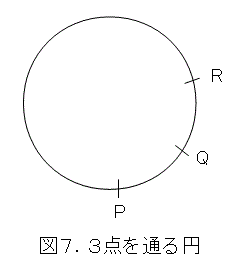
こうして、曲線上から一直線上にない3点を取って、それを通る円なら一意に定まりますね。ちなみに、2章では曲線を直線で近似していましたが、今度は、曲線を円弧で近似しています。
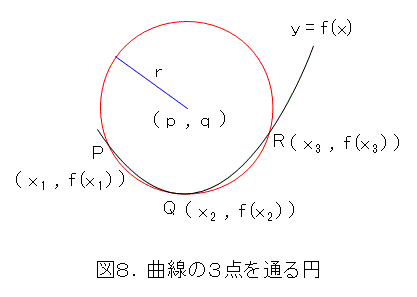
そうしておいて、2点Q、Rを点Pに近づけた極限を取れば一意に定まりそうです。このことは、第2章で扱ったように、曲線の方程式を n 次式とするなら、3重に重複した解と考えられます。
さて、図8で、円の中心と半径は、式(8)、式(9)、式(10)を連立させて解けば求まりますね。
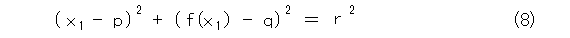
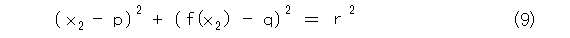
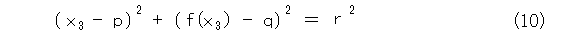
その上で、2点Q、Rを点Pに近づけた極限を取って、一意的に確定することを確かめればよいのですが、さすがに、この計算はやる気がしないなー。もちろん、ちゃんとやりたい人は頑張ってやってみることをお勧めします。
そこで、いつもの荒っぽい方法でやてみましょう。図8で線分PQは曲線の変化を示していますね。折れ線PQRは曲線の変化の更に変化を示していると考えられるでしょう。こう考えると、以下のようにやればよさそうな気がしてきます。
点 ( x , f(x) ) 、 ( x + h , f(x + h) ) が同じ円上に乗っているとすると、式(11)、式(12)が成り立ちます。
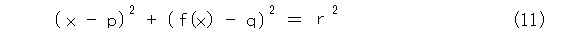
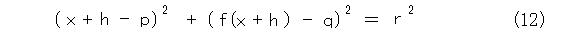
式(12)から式(11)を引いて、
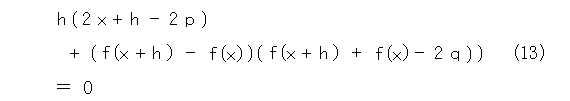
両辺を h で割って、
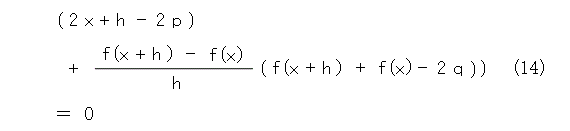
h を 0 に近づけた極限を取って、
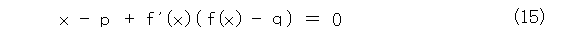
となります。
今度は、式(15)を k だけずらして、
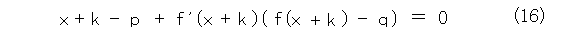
式(16)から式(15)を引いて、
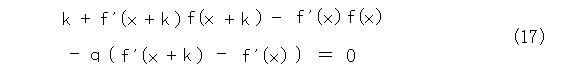
両辺を k で割って、さらに都合よく変形して、
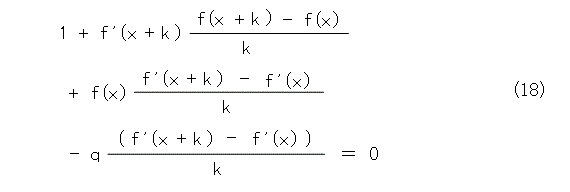
k を 0 に近づけた極限を取って、
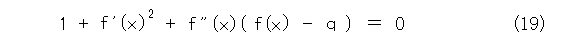
となります。
次に、式(11)、式(15)、式(19)を、 p 、 q 、 r について解いて、
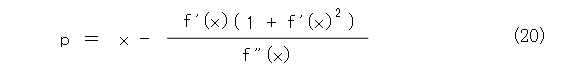
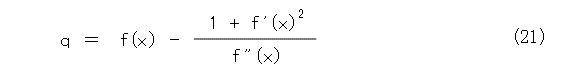
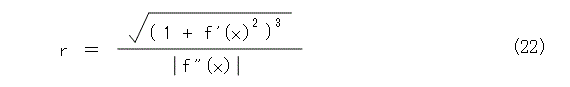
となります。これで、曲線を円弧で近似する円は一意的に定まることが解かりました。この円は特別な名前が付いていて、曲率円と呼ばれています。
曲率円の半径は、曲率半径と呼ばれていて、さらに、曲率半径の逆数は曲率と呼ばれています。これ、「ここのカーブは曲率がどうとかこうとか。」などとよく使う言葉ですね。
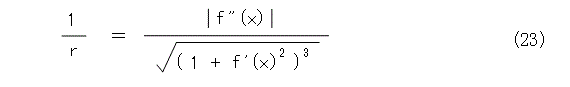
曲率は、円の半径の逆数なので、曲率が大きいほど半径が小さく、曲線は急に曲がっています。色々な曲線で曲率を求めて比較することをお勧めします。
5.おわりに
曲率の話は、大概の微積分の本に書かれています。通常、曲線に2重接触する円ということで曲率円を定義しています。まあ、それでよいのだけれども、あえて、面倒な方法を取ってみました。多少なりとも図形的なイメージが沸いたでしょうか。
ここのところ、余計な手間をかけて、遠回りばかりしています。それによって、色々なイメージが沸いたり、よい思考訓練になったりすると思います。何度も書きましたが、理科好き子供の広場では、舗装道路を進むよりも、遠回りして、でこぼこ道を進み、周りの風景を楽しむということを推奨しています。この点、本稿を読まれた方はどうお考えでしょうか。
完
2021年4月18日
著作者 坂田 明治(あきはる)
|