|
第112話
ヘッセの標準形を考えよう
|

「主な目的」
今回はヘッセの標準形についての話です。ヘッセの標準形を求めたことのある人なら、場合分けや、結果をまとめる際に複号が出てきて面倒になった経験を持っていると思います。本稿では、このような手間を省き、ヘッセの標準形の表記の一意性を目指しています。
本 文 目 次
1.はじめに
3.距離の有向化
6.おわりに
著者 坂田 明治
第112話 ヘッセの標準形を考えよう
1.はじめに
今回は、ヘッセの標準形について考えましょう。
ヘッセの標準形は結構なじみの深い人が多く、「あっ、あれか。」と想像のつく人も多いかと思います。(試験にときどき出るもんね)
一応、ちゃんと書くと、図1のように、原点Oから直線に下ろした垂線の足をH、線分OHの長さを r とし、線分OHと x 軸のなす角を図1のようにすると、直線の方程式は式(1)のようになります。
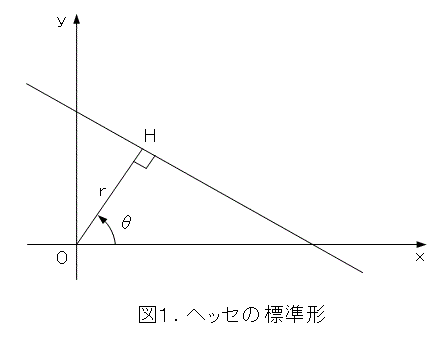
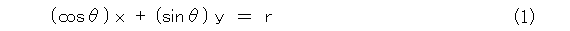
この式(1)がヘッセの標準形です。空間中の平面の方程式に関するヘッセの標準形も似たようなものです。
なお、本稿では、あえて「長さ」と「距離」を混同して使います。これは、慣例によって、線分の長さやベクトルの長さという使い方と、点と点の距離や点と直線の距離などという使い方があり、混同して使ったほうが解かりやすいと思われるからです。
2.平面上の直線のヘッセの標準形
まあ、式(1)のように書くと、すぐ、「三角関数を使うなんてやだな。やっぱり、直線の方程式が式(2)の場合にヘッセの方程式を書いてほしいな。」とケチをつける奴がいますよね。こうなると、必然的に、「そうか、んじゃ、自分でやってみろよ。」と、ケチをつけた奴にやらせるよね。(大体、こういう奴にやらせると破綻することが多い)

とりあえず、 a を正、 b を正、 c を負とします。そうすると、直線の方程式から、図2のようになります。
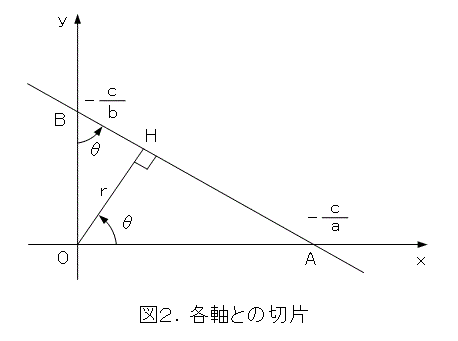
このとき、
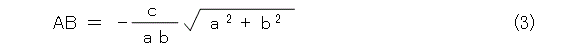

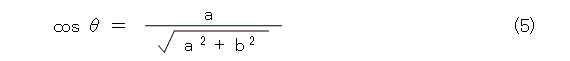
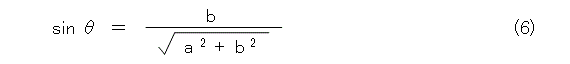
となります。これから、ヘッセの標準形は式(7)の形になります。
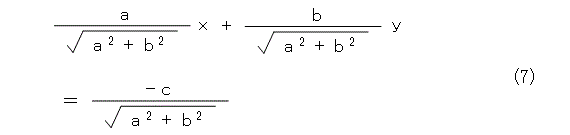
面倒くさいが、場合分けしてまとめると、式(8)のようになります(当然、場合分けと計算は読者の宿題)。ここで、式(1)のヘッセの標準形では、右辺が線分OHの長さなので正か 0 だよね。このことに注意して算出しようね。

ただし、複合は、右辺が正となるように選ぶという条件付です。
とても標準形とは思えないカッコの悪さですね。そういえば、式(8)をよく見ると、 c が 0 のとき(原点を通る直線)はどっちの複合を取ればよいのでしょうか。どっちでもよいなんていうのは、標準形とは名ばかりで、表記の一意性がないのを認めているみたで嫌だな。このままでよいのか。
3.距離の有向化
そもそも、ヘッセの標準形を式(1)だとして、それで終わりにすればよいのに、式(2)を持ち出して、このときにヘッセの標準形を書こうとするからこんなことになるのだ(つまり、言い出した奴が一番悪い)。このままでは気分が悪いので、なんとか解決しようと思いますが、どうでしょうか。(もう、いつものように、やーめたとしたいな)
で、どうあってほしいのかを考えて行きましょう。式(8)のように複号なんて付けないで、式(7)の形に一本化できればいいな。つまり、ヘッセの標準形が、式(9)として一意的に書ければね。
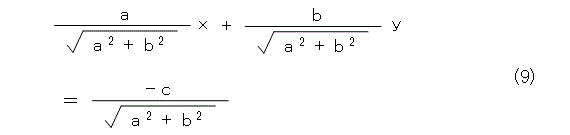
この形なら、式(2)の定数項を移項して、両辺を式(10)で割っただけなので、解りやすいし、式(10)は、それ自体が意味を持っていますね(後で出てくる法線ベクトルの長さ)。

それでは、式(9)がヘッセの標準形になるようにできないかなー。その際に、式(9)をよく見ると、 c が正のときは、右辺は負になるから、距離も負を許すようにしなけれなりません(つまり、距離の有向化)。毎度やってるように、どっかの国で、都合が悪くなると、強引に解釈を変えて辻褄あわせをしているみたいだな。
それで、どこから手をつければいいのか全然解かりません。まあ、とにかく、様子見として、 c が 0 のときから考えましょう。

このときは、原点を通る直線となります。
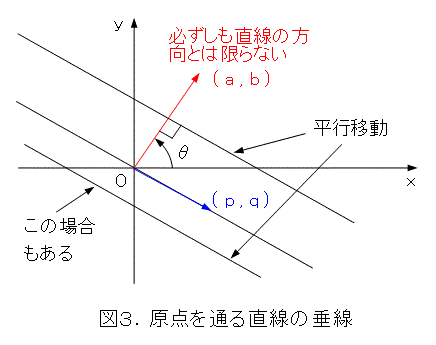
原点から、原点を通る直線への垂線では、何のことか解かりません。そこで、やっぱりいつものゴマカシをして辻褄あわせをします。
原点を通る直線を平行移動して原点から離せば、とにかく垂線が意味を持ってきますね。それで、この垂線を式(11)の直線の垂線としてしまえばよいでしょう。これで垂線が意味を持ったので、これを求めます。式(11)をよく見ると、ベクトル ( a , b ) が直線に垂直であると気づきます(ただし直線の方向とは限らない)。というのは、式(11)の直線上の任意の点 ( p , q ) を取ると、

が成り立ちます。これは、ベクトル ( a , b ) とベクトル ( p , q ) の内積です。内積が 0 だから、この2つのベクトルは垂直です。そうすると、式(11)、を平行移動した式(2)に対して、その係数を取り出して作ったベクトル ( a , b ) は元の直線に垂直です。そこで、ベクトル ( a , b ) を式(2)の直線の法線ベクトルと呼ぶのは合理的ですね。
そうすると、x 軸の正の方向と、法線ベクトルの方向がなす角をもって(つまり、 x 軸の正の方向から反時計回りに法線ベクトルの方向に計った角度)、 x 軸と垂線のなす角とすれば、原点を通る直線でも、垂線と x 軸とのなす角が意味をもってきますよね。
更に、式(10)はベクトル ( a , b ) の絶対値とか、長さとか、ノルムといわれているものなので、式(13)は法線方向の単位ベクトルとなります。
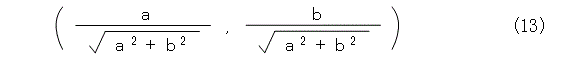
こうして、式(2)を眺めなおすと、式(2)で両辺を法線ベクトルの長さで割って、定数項を右辺に移項したものが、式(9)ですね。要するに、式(9)は式(2)を規格化したものと考えられます。
c が 0 のときを基に、角度の問題は片付いたので、次に、距離の有向化を考えましょう。
とりあえず、原点Oから、式(2)の直線までの距離は、場合分けをちゃんとやって、式(14)となります。(いつものように、これも読者の宿題)

そこで、 a を正、 b を正、 c を負とした直線と、 a を正、 b を正、 c を正とした直線を描き、原点から下ろした垂線の足をそれぞれ、H、Iとします。
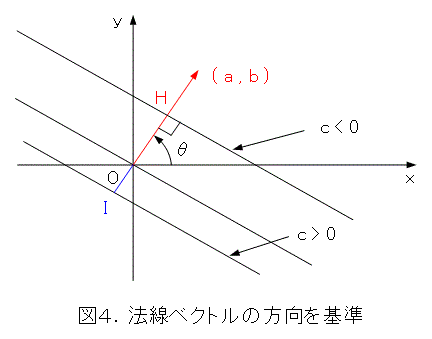
このとき、
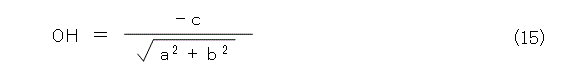
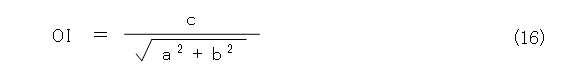
となるので、法線ベクトルの方向を基準として、距離に正負、つまり方向化をすると、式(16)は負の符号をつけなければなりません。つまりこれは、まさしく、式(15)の形になり、ヘッセの標準形は式(9)として一意に定まります。
次に、調子に乗って、任意の点S ( s , t ) から、式(2)の直線までの距離(有向化したもの)を求めてみます。
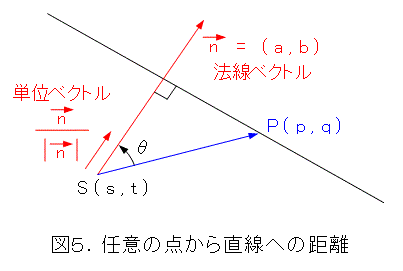
式(2)の直線上に適当に点P ( p , q ) を取ります。そのときに、式(17)が成り立ちます。

こうすると、法線ベクトル方向の単位ベクトルを使って、内積で直線までの距離を表すことができますね。式(18)の最初の式が距離で、それを成分計算したものが第2の式で、式(17)を代入したものが第3の式です。
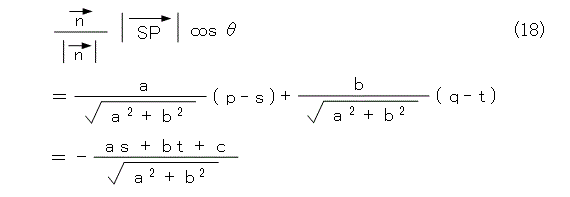
したがって、 任意の点S ( s , t ) から、式(2)の直線までの距離は式(19)となります。
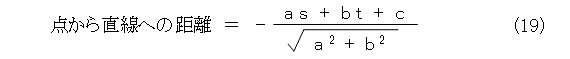
これから、式(2)の直線から、任意の点S ( s , t ) までの距離は、向きが逆になり、式(20)となりますね。(いやー、ここまできて、以下のことに気づいて辻褄合わせのためにやったんだな)
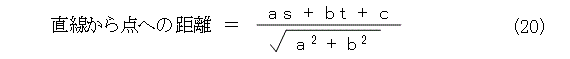
さて、式(2)の直線によって平面を正領域と負領域に分けたものが図6です。
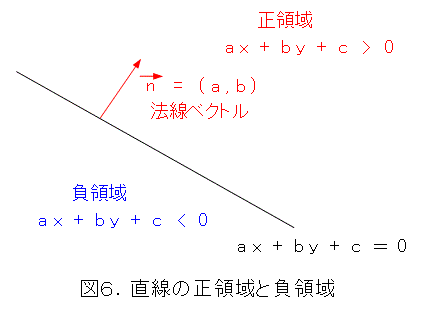
図6において、式(20)によって、直線から点までの距離の正負で分類すると、丁度、距離の正負と、領域の正負が一致します。これで法線ベクトルによって距離の向きを付けることは有効であると確認できましたね。(よかったことにしてごまかしている)
4.2直線の交角の2等分線
距離の有向化ができると、2直線の交角の2等分線が簡単に求まります。この問題も、ときどき試験に出ます。これ、落とし穴があって、それに引っかかるのを楽しんでいる教師がいました。
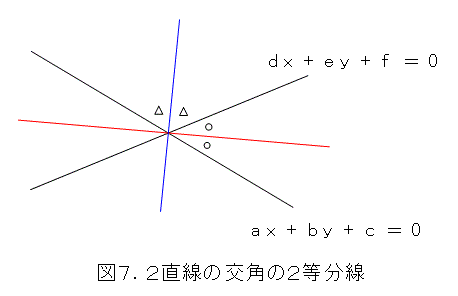
図7のように、実は交角の2等分線は2本あります。これを見落として、1本しか求めない人がいるので、この教師は面白がって(?)出していたようです。
図7のそれぞれの直線から点 ( x , y ) までの距離は、それぞれ式(21)、式(22)となります。


そこで、図7の2直線で区切られた4つの領域は、直線からの距離が、正正、正負、負正、負負の4通りになります。そうなってくると、この組み合わせで距離が等しいときを書くと、次の式(23)、式(24)ですね。
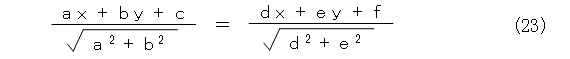
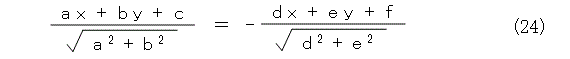
あとは、それぞれ左辺に移項して整理すれば直線の方程式が求まりますが、書くのが面倒なので以下省略。(ちゃんと書き下すのが読者の宿題)
5.空間上の平面のヘッセの標準形
今度は、空間中で平面のヘッセの標準形を考えましょう。これもよく試験に出る問題ですね。
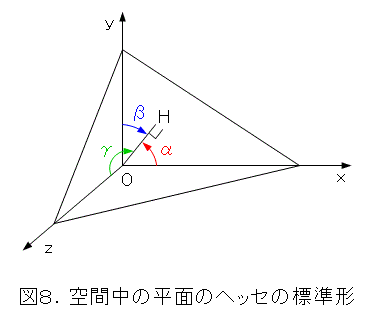
原点Oから平面へ垂線の足Hを下ろし、線分OHの長さを r 、線分OHと x 軸、 y 軸、 z 軸のなす角を図8のようにすると、ヘッセの標準形は式(25)となります。
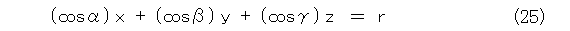
ここで、図1でも、図8のように角を取れば、式(1)は式(25)と同じ形になりすね。
さて、平面の方程式が式(26)で与えられたときを考えましょう。
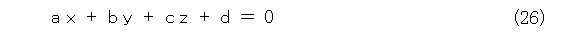
このときに、ベクトル ( a , b , c ) が式(26)による平面に垂直であることは、直線の場合と全く同様です。したがって、ベクトル ( a , b , c ) を平面の法線ベクトルと呼ぶのは妥当ですね。そして、法線ベクトルの方向を基準として、距離に正負、つまり方向化をするというのも直線の場合と全く同様です。こうして、直線のときと全く同様にして、ヘッセの標準形は式(27)のようになります。
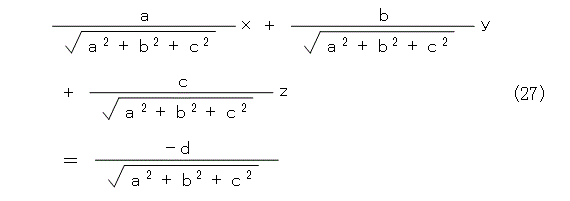
また、点と平面の距離も直線のときと全く同様です。書くまでもありませんね。
6.おわりに
今回は、ヘッセの標準形について考えました。その中で、距離の方向付け(正負の意味付け)を行うことによって取り扱いが簡単になり、特に、場合分けなどを回避できることを見ました。こういうことは、いつでもうまく行くとは限りませんが、それでも考えてみる価値はあります。例え失敗し、何も得られなかったとしても、思考訓練としての意味はあると思います。
よく、「地道にやらなければいかん。」とか、「楽をするな。こつこつとやれ。」などと言う人がいますが、楽をするために頭を使い、工夫をするというのも、よい思考訓練であり、重要なことだと思います。この点、本稿を読まれた方はどうお考えでしょうか。
完
2022年2月20日
著作者 坂田 明治(あきはる)
|