第１１３話

　部屋割り論法を考えよう

　

「主な目的」

今回は部屋割り論法についての話です。部屋割り論法は感覚的で解かりやすい方法です。例えば、５人で旅行したときに、４部屋しか空きがなければ、どれか１部屋に２人泊まることになります。これが部屋割り論法です。常識的で、簡単な考えですが、意外と役に立ちます。本稿では、部屋割り論法を通して、身近なところにある単純な方法についての考察を行います。

　

　

本　文　目　次

　１．はじめに

　２．部屋割り論法

　３．閉区間 [ 0 , 1 ] での応用例

　４．無限個の場合

　５．おわりに

　

著者　坂田　明治

　

　

　

第１１３話　部屋割り論法を考えよう

　

１．はじめに

　今回の話題は、部屋割り論法です。こう書くと、「あー、あれか。電車の席取り合戦のことか。」と思う人も多いかと。一応、念のため、電車の席取り合戦を書いておくと、例えば、電車の席が３２で、乗ってきた人が３３人のときに、必ず、１人はあぶれるというものです。まあ、これは始発か、始発に近い駅でよく起こることで、いつも途中駅で乗って立ちっぱなしの著者には関係ないことです。

　

　では、なんで、今回この話題にしたかといえば、草刈中の出来事が原因です。だいたい、何も考えず、どこでも空きがあればやたらめったらと植物を植えやがって、そのせいで草刈が非常に面倒じゃないか。そもそも、どこに何が植えてあるのか解からず、植えたやつと思われる植物を避けて草を刈るのがどれだけ大変なことか解かっているのか（こうこう、やたらと植物を植えるのに限って、「邪魔になったら切っていいよ。」というけれども、本当に切ると怒る）。滅茶苦茶でゴチャゴチャしている植物のせいで、「こいつら、席取り合戦で割り込んできた連中と同じじゃねーか。」と炎天下で暑くてたまらない上に、更に頭がカッカしていました。よく熱中症にならなかったもんだ。ということから、今回は部屋割り論法にすることを決めました。

　

　ちなみに、特に、始末したいと思っている植物は以下です（まあ、あまり見たくないと思うが）。まずは、通称トゲツルグサといわれている「カナムグラ」と「イシミカワ」。こいつらには、さんざん痛い目に遭わされたので個人的恨みから、見つけ次第引っこ抜いて処分。発芽期が限られているので、見落としさえしなければいいが。

　

　つぎは、ガビガビソウこと「コセンダングサ」。果実というか、種がなっている状態というか、とにかくその写真を見ればガビガビのいわれが解かります。服にやたらとくっついて嫌な思いをしたし。同じ位嫌なのが、ノラカボチャこと「アレチウリ」です。これは、どっかのサイトで「ノラカボチャではありません。」と書いてあったので、面白がってノラカボチャと呼んでいます。こいつ、花が咲くとスズメバチが来るので危険です。で、こいつらは、見つけ次第引っこ抜いていますが、抜いても後から後から出芽するのでやっかいです（一体、種がどれ位あるんだ）。

　

　あとやっかいなのは、ビンボウカズラこと「ヤブガラシ」です。こいつも花が咲くとスズメバチが来るし、根が残るとまた生えてくるし、根は取りきれないし、多年草だし。他にもまだ沢山あるけど、まあ、いいや。

　

　

２．部屋割り論法

　さて、部屋割り論法というのは、 n 個より多くのものを、 n 個の部屋に押し込むと、どこかの部屋に２個以上押し込むことです。

　

　例えば、７本の植物を６個の鉢に植えようとすると、どれかの鉢は２本の植物を植えなくてはなりませんね。

　

　

　部屋割り論法が成り立つことは、背理法で確かめられます。つまり部屋割り論法が成り立たなかったとして、どの部屋も１個しか入ってないとします（０個しか入ってない部屋を考えてもよいが、話は同じ）。

　

　まず、 n 個より多くのものを m 個とします。つまり式１です。

　

　

　n個の部屋に押し込むとき、どの部屋も１個しか入ってないので、１を n 個の部屋に渡って足し合わせること、つまり、１の n 倍が元の個数 m になるはずですね。ところが、

　

　

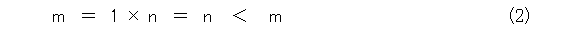
となって矛盾します。したがって、部屋割り論法が成り立ちます。

　

　このように、部屋割り論法は大したことのない論法のように見えますが、部屋割り論法の使い方に気が付かないと七転八倒の苦しみを味わうことがあるため、案外試験によく出ます。例えば、次のような問題です。

　

　n + 1 個の整数があるときに、ここから２個の整数を適当に取ると、その差が n の倍数になる。

　

　まず、第１感は、「これは、出題者の性格が悪く、場合分けを怠ると減点するに違いない。」ということでしょうか。つまり、場合分けに目を向けさせ、部屋割り論法に気付かせない策略ですね。ここでは、部屋割り論法のことをコチャコチャ書いているので、この種の罠はかけられないけど。

　

　それで、まずは、 n + 1 個の整数を並べます（なんでもいいから適当に並べる）。それを、

　

　

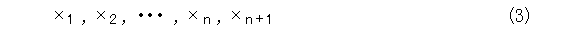
とします。このうち、等しいものがあったとして（重複のある場合）、

　

　

とすれば、

　

　

となるので、その差は n の倍数ですね。

　

　上記のように、整数に等しいものがあれば成り立つので、そうでない場合、つまり、 n + 1 個の整数が互いに相異なるときを考えましょう。

　

　大体、話の流れからして、ここで部屋割り論法が出てくるのは明白ですね（罠のかけようがない）。その上、 n + 1 個の整数なんて、とって付けたような個数を見れば、 n 個の部屋を用意するというのが見え見えです。

　

　さて、整数は以下のように表すことができます。

　

　

ここで、 r は n で割った余りなので、 0 から n - 1 までの整数です。

　

　そこで、 n で割った余りで部屋割りをすると、部屋の数は丁度 n 個になります。そうすると部屋割り論法によって、同じ部屋に入る整数が少なくとも２個存在します。同じ部屋に入るということは、 n で割った余りが等しいということなので、その２整数は以下のように書けます。

　

　

　

　式（７）と式（８）の差をとって、

　

　

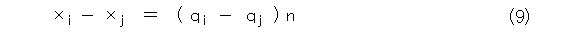
となるから、差が n の倍数になりますね。

　

　

３．閉区間 [ 0 , 1 ] での応用例

　今度は、閉区間 [ 0 , 1 ] 上の、相異なる位置に n + 1 個の点をばらまけば、２点間の距離が 1/n 以下になるものがあるかという問題を考えてみましょう。それにしても、タイトルからして部屋割り論法なんで、最初から部屋割り論法を使えばできるというのが見えてしまっているなー。しかも、 n + 1 個なんてわざとらしくて、これで、 n 個の部屋を作ればよさそうだ、というのまでばれてしまっている。

　

　とにかく、 n + 1 個の点があるのだから、小さい順に、

　

　

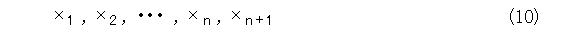
としましょう（さっきの式（３）と全く同じだけど、今度は小さい順だ）。

　

　さて、閉区間 [ 0 , 1 ] を n 等分して、 n 個の部屋を作ります。

　

　

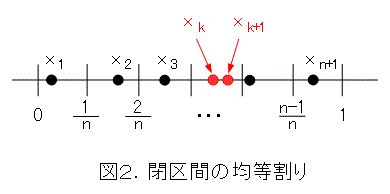
　すると、部屋割り論法によって２個以上の点が入っている部屋があるので、それを図２のようにします。ここで、 n 等分した各部屋の大きさは 1/n だから、式（１１）が成り立ちます。

　

　

　したがって、２点間の距離が 1/n 以下になるものの存在が示されました。めでたし、めでたし。

　

　と納得した人は罠にかかっています（やったね）。あえて書かなかったけど、部屋割りというのは、互いに共通部分を持っていません。

　

　図２では、閉区間 [ 0 , 1 ] を n 個に部屋割りするようなフリして、 n 個の閉区間に分割しており、各区間の端点が共有されています。無理矢理半開区間にするという手もなくはないが、これだと区間の端点の扱いが面倒なのでやりたくありません。

　

　

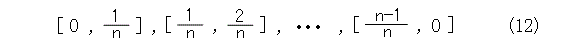
　式（１２）のように書けば、確かに、各区間の端点共有が見て取れます。そうなると、気楽に部屋割り論法を使ったのでは、正しい推論とはいえなくなりますね。

　

　そうすると、対策は３つ考えられます。まず、思いつくのはあきらめることです（おすすめ！）。あきらめられない人は、他の方法を考えなくてはなりません。そこで、第２の方法として、部屋割り論法をやめるというのが考えられます。これ、背理法を使っても簡単にできるので、読者の宿題ですね。第３の方法は、部屋割り論法を拡張して、上でやったやり方がそのまま使えるようにすることです。

　

　今まで、部屋割り論法を、わりと感覚的に捉えてました。これは、例えば、４人で旅行に行ったときに、幹事の手落ちで、３部屋しか予約されてなく、しかも、その旅館には空き部屋が無いため部屋の追加ができず、この３部屋のうち１部屋を相部屋にするという状況でした（当然、幹事はボコられる）。

　

　

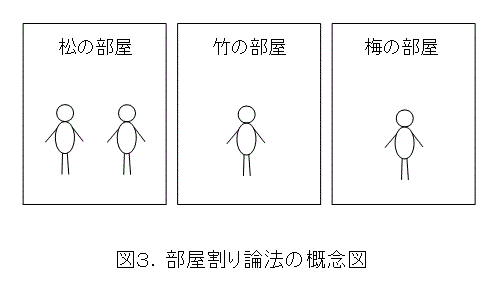
　部屋割り論法を拡張するために、もう少し正確に記述しましょう。図３をよく見ると、部屋の役割は泊まりに来た４人を３つに分けることのみです。部屋の高級感や料金などは関係ありません。そう考えると、４個の要素よりなる集合を、３個の部分集合に分けるということになりますね。その際に、各々の部分集合は、互いに共通部分を持ちません（２部屋に、同時に泊まれる人はいないから）。

　

　この状況から、元となる集合Mに対して、その部分集合を部屋割りとみなすには、以下のようになっていると考えるのが自然でしょう。（これを類別という）

　

　

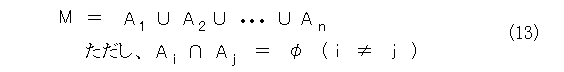
　こう考えると、拡張するのは簡単ですね。閉区間 [ 0 , 1 ] でも使えるように、式（１３）のただし書きを削除するのが見えています。更に、式（１３）の等号も包含関係にすればなおさら拡張されます。（これを被覆という）

　

　

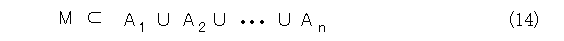
　もっともっと拡張するために、Mの要素全てではなく、対象となる要素に限定したらどうでしょう。

　

　つまり以下のように、部屋割り論法を書き直してはどうでしょうか。

　

　集合Mを n 個の集合で被覆したときに、集合Mから、 n 個より多くの要素を取ると、被覆をした集合のどこかに２個以上の要素が入っている。

　

　こうして拡張された部屋割り論法が成り立つことは、普通の部屋割り論法と全く同様に示せますし、その結果、本章で扱った問題の解決策が、全く変更を加えることなく使えます。

　

　

４．無限個の場合

　今までは、部屋の数は有限、対象となる要素（点）の個数は有限でした。ここでは、これらを無限個にした場合について考察しましょう。

　

　まずは、部屋を無限室にします。部屋割り論法は、部屋の数より多くの人がいるときに、無理矢理部屋に押し込むと、２人部屋が出てくるというものでした。ということで、部屋が無限室の場合には、無限人が対象となりますね。その上で２人部屋が出てくるかということを考えてみましょう。

　

　これには、無限室を持つ宇宙ホテルとがめつい支配人ガメツを考えるのがよろしいかと。宇宙ホテルが満室だったときのことです。運悪く、新規の客が泊まりに着ました。金に汚いガメツは、ここでこの新規の客も、何とかして泊めてしまったほうが宿泊代が儲かるし、そもそも、満室だからといって宿泊を拒否すると、SNSで満室だということは出さずに、一方的に宿泊拒否の悪口を叩かれ、評判が悪くなり、客が来なくなって儲からなくなると考えました。

　

　そこで、１号室の客を２号室へ移し、新規の客を１号室へ泊め、２号室の客を３号室へ移し、１号室の客を２号室へ泊め、３号室の客を４号室へ移し、２号室の客を３号室へ泊め、以下同様に部屋を移しました。こうすれば、全員１人部屋に泊まれます。ガメツは、金のためには、宿泊客の都合なんて考えていないもんね。

　

　

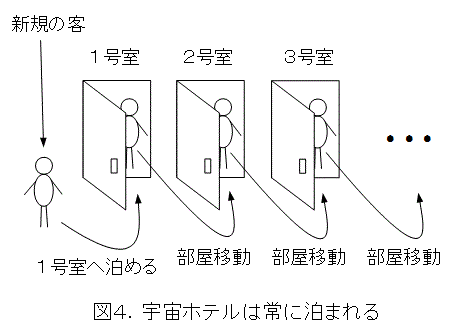
　こうして、ガメツは全員を１人部屋に泊めて、がめつく全員から宿泊料金を徴収しました。

　

　以上から、部屋が無限にあったのでは、うまく部屋割り論法が使えないことが解かりましたね。

　

　つぎに、部屋の数は有限室として、対象となる要素の数が無限個の場合を考えましょう。無限個を有限の部屋に押し込めたら、どこかの部屋に無限個入らねばならないのは明らかですね（どの部屋も有限個なら全体が有限個になるから）。こんなのが何か使い道があるのかと思うでしょうが、使い道はあります。例えば、以下のような場合に役に立ちます。

　

　閉区間 [ 0 , 1 ] 上の、相異なる位置に無限個の点をばらまけば、相異なる点からなる収束点列が存在する（この点列の極限を集積点という）。

　

　これを示すには、以下のように部屋割り論法を使います。

　

　最初に、

　

　

とします。ここにばらまいた無限個の点があります。

　

　次に、この区間を２等分すると、少なくとも、そのどちらかには無限個の点があります。無限個の点のある方を適当に選んで、

　

　

とします。今度は、これを２等分して、無限個の点のある方を適当に選びます。以下同様に、前の区間を半分にして無限個の点のある方を適当に選び、区間列を作ります。

　

　

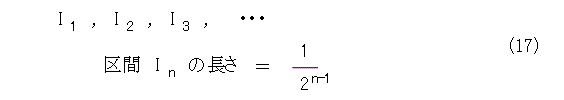
　こうすると、式（１７）の閉区間列は、縮小閉区間列となり、１点に収束します。このとき、収束する点を a とします。

　

　

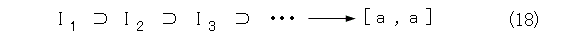
　式（１８）の各区間は、元のばらまいた点を無限個含んでいるので、それぞれから、適当に点を選びます。この際に、選ぶ点は、それ以前の各区間で選ばれた点とは別の点を選びます。それぞれの区間には無限個の点があるのだから、これは可能ですね。こうすれば、互いに相異なる点列が作れるでしょう。そして、この点列は a に収束します。

　

　

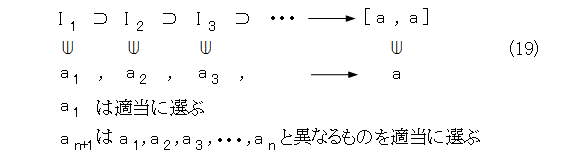
　こうして、 相異なる点からなる収束点列の存在が示されました。

　

　

５．おわりに

　１つの席に対して２人の人がいれば、どちらか１人があぶれるか、２人で1つの席に座るしか手はありません。これは、子供でもよく経験しています。このことから、部屋割り論法は、感覚的に解かりやすい、簡単な論法です。しかし、こんな部屋割り論法が意外と役立つということを見てきました。これから、感覚的によく感じていることでも、よく考えると、色々と使え、役に立つものがあるといえるでしょう。もちろん、いつでもうまくいくとは限りませんが、身近にある単純なことや方法をよく考えてみるのは面白いし、よい思考訓練になります。この点、本稿を読まれた方はどうお考えでしょうか。

　

完

　

2022年8月20日

著作者　坂田　明治（あきはる）