|
第115話
漸化式を連立化してみよう
|

「主な目的」
今回の対象者は、線形連立漸化式、行列、行列のべき乗に興味を持っている方です。具体的に扱う内容は、線形連立漸化式の行列表示、行列の固有値から行列の対角化または三角化によって線形連立漸化式の解を表示することです。式変形などにとらわれることなく、考え方の流れを楽しみましょう。
本 文 目 次
1.はじめに
2.ツルカメ算
3.漸化式の連立化
4.連立漸化式を解く
5.おわりに
著者 坂田 明治
第115話 漸化式を連立化してみよう
1.はじめに
第114話では、2階1次の漸化式や3階1次の漸化式を解きました。今回はもっと楽して解けないかを考えてみましょう。つまり、式(1)の漸化式を腕力による力詰めではなく、もっとカッコイイやり方で解けないかということです(この際、計算が面倒になっても目をつぶる)。要するに、中身はともかく、見た目だけよければよいとします(人間を見た目で判断すると危険なので、なんか落とし穴がありそう)。

それで、なんか見た目だけキレイな例がないかと考えると、連立方程式の書き方を思いつきました。

式(2)の連立方程式は、ごちゃごちゃしているように見えますが、行列を使って書き直すと式(3)のように見やすくなります。
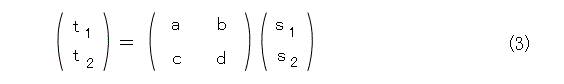
更に、式(4)のように置くと、
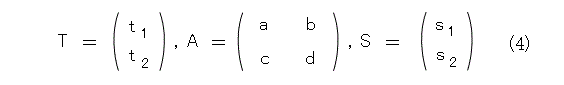
式(5)のように極めて簡単になります。

中身は式(2)のままですが、なんか簡単になったような気がしますね。以下、この手を使って考えましょう。
2.ツルカメ算
おそらく、最初に連立方程式を習うのは、ツルカメ算だと思います。次の問題を考えましょう。
「ツルとカメが合わせて10匹(ツルは1羽、2羽って数えるんじゃないか)。ツルとカメの足が全部で26本ある。ツルは何羽でカメは何匹か。」
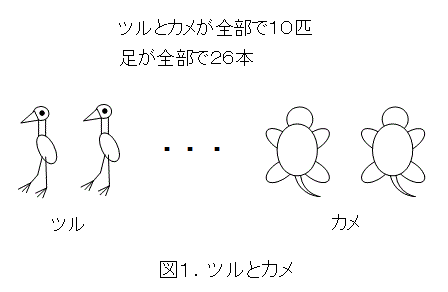
この問題を解くのに使われるのが、ツルカメ算という残虐非道な方法です。まず、ツルとカメから足を2本ずつ切り落としてしまいます(こんなことをしたら怒られるよな)。
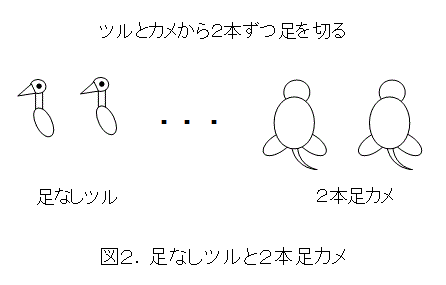
するとツルとカメは全部で10匹ですから、足を20本切り捨てることになります。足は全部で26本だから、20本切り捨てた残りは6本ですね。そして、カメは2本足なので、6本の足の半分がカメの数となります。つまり、カメは3匹です。

ツルとカメ全部で10匹だったので、3匹がカメなら残りの7羽はツルとなります。こうしてツルカメ算が完成します。
こんな足を切るなんて方法は使いたくないよね(ちなみに、ツルの代わりにアヒルを使えば、足を羽の中に引っ込められるので、ツルとカメが2本ずつ足を引っ込めればよくなり、問題なし)。そこで、ツルの数とカメの数を文字化してみましょう。つまり、ツルを x 羽、カメを y 匹とします。そうすれば、 ツルとカメが合わせて10匹、ツルとカメの足が全部で26本は式(6)と書き表されます。

こうすることによって、式変形だけで解くことができます。やり方は色々ありますが、第1式を2倍して、第2式から引けばカメの数が求められます(ツルカメ算と同だけど、足を切るという行為をしなくて済む)。
とにかく、連立方程式化すれば、足を切るなんて、余計な行為を想定しなくてもよくなり、機械的な計算で求められます。うまく使えるようになると、色々役に立ちそうですね。
3.漸化式の連立化
さて、式(1)の漸化式を連立化してみましょう。それには、文字をもう1個導入すればよいので、簡単に考えて、式(7)のようにしてみます(失敗したら考え直す)。

すると、式(1)は、式(8)、式(9)と連立化されます。
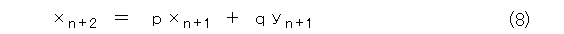

これだとカッコ悪いので、式(8)の項番号をずらして書き直します。
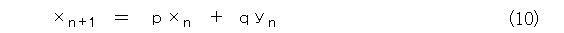

式をながめていると、もっと一般的に拡張したくなるでしょう。
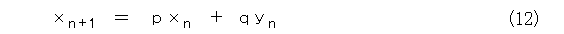
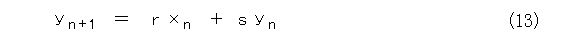
行列を使うと、もっと簡単ですね。

連立1次方程式を扱うときに、いつも付いているただし書きがあります。これ、ただし書きの式が 0 になるとして、式(12)を s 倍したものから、式(13)を q 倍したものを引けば、理由を納得できます。自分で実際に式を書いて確かめましょう。
更に、式(15)のようにおきます。
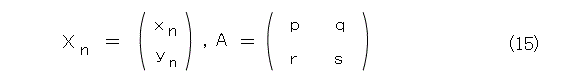
すると、等比数列と同じ形になりました。

これから、等比数列のときと同じように、一般項が求められます。
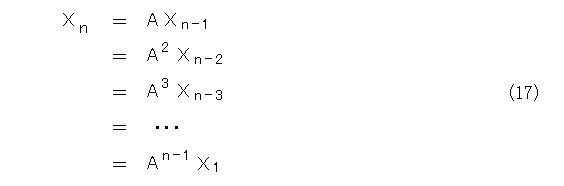
もちろん、力詰めで式(14)を解きたい人は、式(12)、式(13)から頑張って解きましょう。その際に、式(13)は式(11)を一般化したとはいえ、出発点で、文字を追加導入して、項番を1つ下げたことを思い出しましょう。つまり、式(8)を復活させます。そうして、式(13)を式(8)へ代入したものと、式(12)を連立させると、1つの数列だけの2階1次の漸化式が得られます。これから、第114話でやったようにして解けます。当然、これは読者の宿題です。
4.連立漸化式を解く
ここにきて、「はじめに」の冒頭で書いた落とし穴にはまっていることに気付きました。行列のべき乗を計算しなくてはなりませんが、これ、第102話で面倒になって手抜きした(というよりもサボった)話です。どうしよう。
行列のべき乗を計算しようと思っても、行列の積はグチャグチャで、とてもまともに扱えるものではありません。とりあえず、2次の正方行列の積を書いてみましょう。
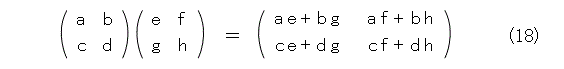
もう、見ただけでべき乗なんて考える気がしません。こういうとき、さっさとやめるのが第1選択ですが、まあ、諦めず(諦めると文句言う奴がいる)、とりあえず、2乗を計算してみましょう。
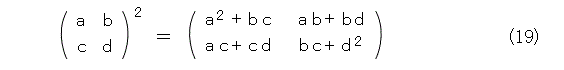
やっぱり、グチャグチャですね。複雑過ぎて手が出ないときは、簡単なもので様子をみるのが手です。一番簡単なものはゼロ行列(成分が全部 0 )で、次に簡単と思われるのは単位行列です。これらは2乗しても同じ行列になります。その次に簡単なのは対角行列でしょう。実際に2乗してみます。
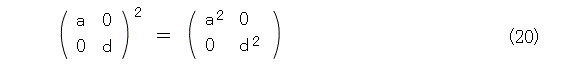
なるほど、これならべき乗計算に都合がよくなります。そこで、元の行列を、何とかして、対角行列に変換できればよさそうな気がします。
では、どうしましょうか。まず、元の行列をAとして、それを対角行列Tに変換するとはどういうことでしょうか。行列は1次変換、つまり、写像なので、Aの定義域をTの定義域、 Aの値域をTの値域に写し、その上で、写像Aを写像Tへ移していると考えねばなりません。そう考えると、対角行列Tでの写像は、座標変換をPとして、まず、座標変換Pで平面を平面に変換し、次に、行列Aで写像し、その結果を逆座標変換P-1で戻したものと同じ作用をするということになります。
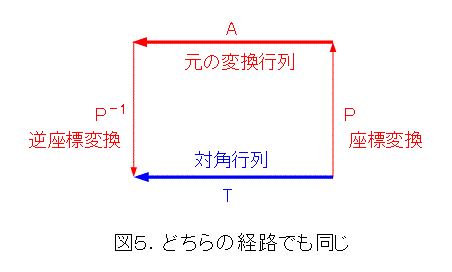
これを式で書いたものが、式(21)です。

Aについて解くため、式(21)の両辺に、左からPをかけ、右からP-1をかけると式(22)となります。

こうしておいて、PとTを定めることを考えましょう。そのために、PとTを以下のようにおきます。
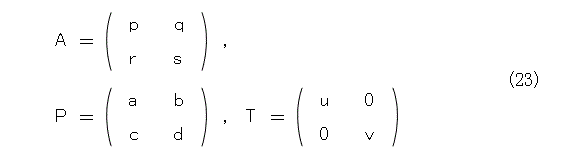
さて、今のところ何の手がかりもないので、とにかく何かやってるフリだけはしてみましょう。問題の対角行列は、単位行列のスカラー倍からどの位かけ離れているかを考えましょう(こんなダメっぽいことするのは、手詰まりでやけくそになってるから)。とりあえず、単位行列のスカラー倍を引いてみます(この評価をするなんらかの基準が必要になるだろうな)。つまり、式(22)の両辺から t E(Eは単位行列)を引いて様子を見ましょう。
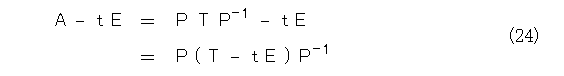
式(24)を見ていると、両辺の行列式を取れば、うまいことにPとP-1が消えますね。
ここで、行列式というのは、行列Qに対して、式(26)のように成分による計算値を対応させることです。

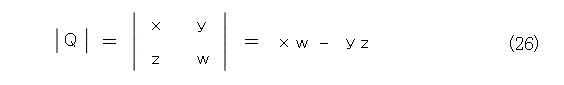
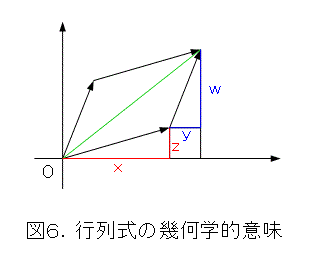
行列式の幾何学的意味は、式(25)の列ベクトルが作る平行四辺形の面積(正負を付ける)です。図6を参考にして、平行四辺形の面積を計算し、正負の意味を調べるのは読者の宿題です。
更に、Rを行列とすると、式(27)が成り立ちます。この検証は読者の宿題です。

この式が成り立つと、

だから、
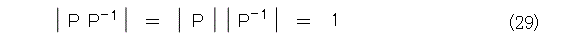
となります。
すると、式(24)で両辺の行列式を取って、

が出てきます。
この行列式を成分で書きましょう。
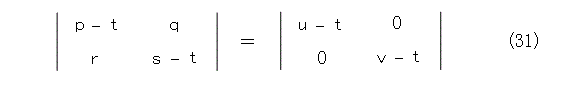
ここで、対角行列が、単位行列のスカラー倍とどの位かけ離れているかの評価を行列式によって行います。行列式を基準として、対角行列が、単位行列のスカラー倍と一致しているとすれば、式(30)は 0 ですね。つまり、式(31)が 0 です。
そこで、式(31)を計算した上で、式の値を 0 とおいてみましょう。
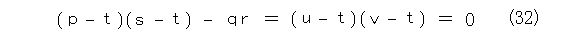
式(32)を固有方程式、その解を固有値と呼びます( t についての方程式)。更に、式(32)は2次方程式で、その解は、 u 、 v であり、式(23)から、行列を対角化すると、固有方程式の解が対角成分に並ぶということが見て取れます。なお、式(32)の左辺を計算すると、式(14)のただし書きから、 u 、 v とも 0 ではありません。自分で確かめましょう。
しかし、ここまでのやり方はかなりテキトーだったので、本当に対角化できるかどうかを調べる必要があります。実際に対角化が可能かどうかは、式(21)、同じことですが、式(22)のPがちゃんと選べるかどうかです。逆行列を求めるのは面倒なので、式(22)の代わりに、式(33)を考えましょう。

ただし、Pは逆行列を持たねばならないので、式(34)が成り立たねばなりません。この確認は読者の宿題です。
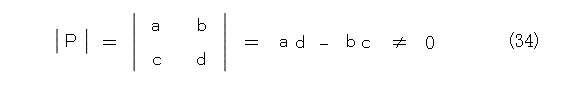
式(33)を成分で書くと、式(35)になります。
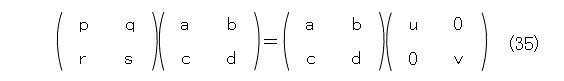
成分を計算した結果が式(36)です。
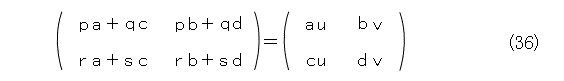
式(36)の成分を比較して、ちょいと右辺の文字の順序を入れ換えたものが、式(37)、式(38)、式(39)、式(40)です。




これらの式は p 、 q 、 r 、 s についての場合分けを考えなくてはなりませんが、以下では、式(41)の場合についてのみ扱います。そうでないときは、自分で調べましょう。

これは、式が4本に見えますが、式(37)と式(39)は固有方程式(32)の解が u であることから同じ方程式になります(たとえば、式(37)を c について解いて、式(39)の左辺から右辺を引いたものに c を代入し、固有方程式(32)の解が u であることを使えば 0 になるから)。式(38)と式(40)も同様です。したがって、実際は式(37)と式(38)の2本だけです。これから、適当に、 a 、 b 、 c 、 d を選べばPが作れます。ただし、Pが逆行列を持つことから、式(34)が成り立たねばなりません。
式(37)、式(38)をそれぞれ c 、 d について解いて式(34)へ代入しましょう。
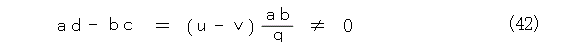
これから、 u と v は異なること、つまり固有方程式(32)は異なる解であるときに、Pは逆行列を持つことが解かります。そして、式(37)、式(38)、式(39)、式(40)を満たすように、たとえば、式(43)みたいに、 a 、 b 、 c 、 d を選びます。
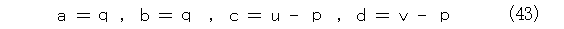
するとPは式(44)のようになります。
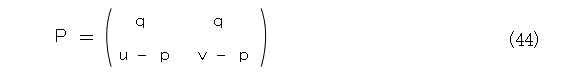
これから、Aは式(45)のように書けます。
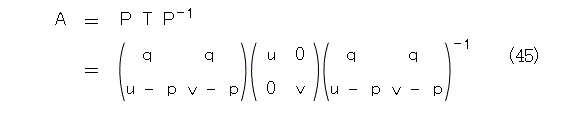
したがって、Aの n 乗は以下です。
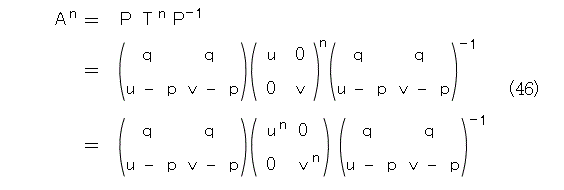
式(15)、式(17)と式(46)とから、固有方程式が異なる解を持つときの一般項が求まります。
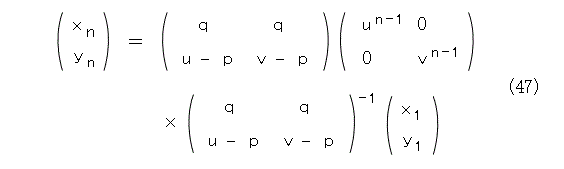
あとはただの行列計算なので、実際にやってみることをお勧めします。
今度は、固有方程式が重解を持つときを考えましょう。つまり、ここでのやり方では、うまく対角化できないときに、どうするかということです。
立ち返ると、元々は、式(17)が計算できること、つまり、行列のべき乗が計算できることでした。ということは、対角行列にならなくても、べき乗が計算できる行列であればよくなります。どんな行列がよいか考えてみましょう。
対角行列は、対角成分の他が 0 でした。具体的には、12成分と21成分が 0 です。少しゆるめて、どちらか片方のみ 0 としてみましょう。どちらでも同じなので、21成分を 0 とします。そうすると、たとえば、式(48)のような行列です。

式(48)のべき乗を少し書いてみましょう。
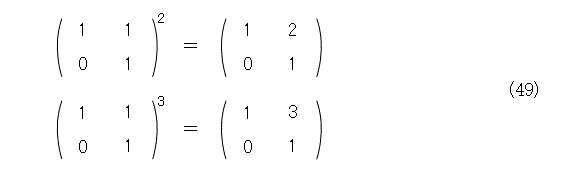
これから、式(50)が予測されます。あとは帰納法で調べるだけです(読者の宿題)。
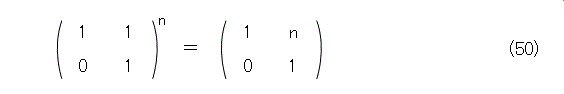
このことから、式(51)のような行列になればいいな、と思ってしまいます。

対角成分が u なのは、固有方程式が重解を持つことから、それらが対角成分に並ぶのではとの期待です。12成分が u なのは、なるべく面倒なことにならないでほしいとの期待からです。
こうするとべき乗は簡単に計算できて、式(52)のようになります(なんか、ものすげー簡単になった)。
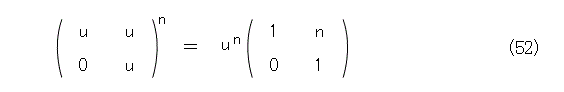
そこで、式(53)のようにおいて、式(54)が成り立つようにできるかどうかです。
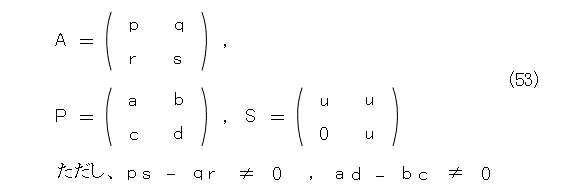

式(54)から、式(55)が出ます。

そこで前にやったように、 単位行列のスカラー倍を引きます。
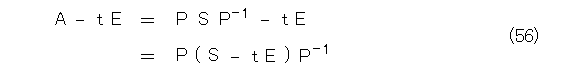
両辺の行列式を取って、
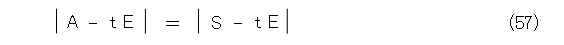
成分表示すると、
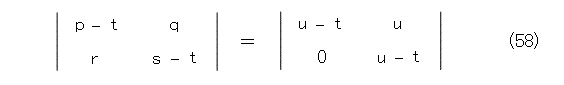
式(32)と同様に、これを 0 とおいてみます。
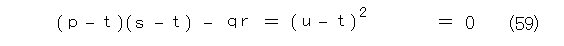
式(32)と全く同様の式が現れました(固有方程式)。違いは、 u を重解(固有値)としている点です。この場合も、式(53)のただし書きから、解は 0 ではありません。
あとは、式(60)を満たすようなPを見つけるだけです。これは、自分でやりましょう。

ともかくPが求まったとします。そのときに、式(61)のようになります。
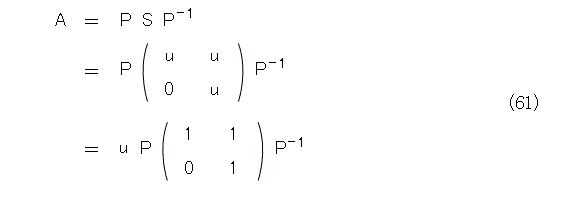
これから、べき乗は以下のように計算できます。
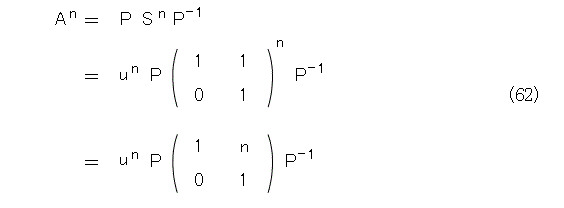
式(15)、式(17)と式(62)とから、固有方程式が重解を持つときの一般項が求まります。
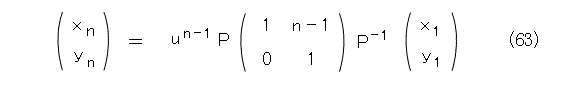
5.おわりに
第114話では、2階1次の漸化式を力詰めで解きましたが、今回は、見方を変えて、連立化して考えてみました。連立化すると、等比数列と似た状況になり、自然に、行列のべき乗を求める問題になりました。そして、都合よく計算できるようにしたいという思いから、何らかの基準の下で同じになることを考えました。
このように、見方を変えるということは、有意義であると思われます。たとえ、うまく行かなかったとしても、そこからなにも得られなかったとしても、無駄にはなりません。考えること自体が思考訓練として意味のあることだからです。この点、本稿を読まれた方はどうお考えでしょうか。
完
2023年4月29日
著作者 坂田 明治(あきはる)
|