|
第90話
ひもの波の話
|

「主な対象読者」
今回の主な対象読者は高校生以上です。ある程度の数学的知識を必要とします。しかし、絵を多用していますので、中学生以上なら、概観を眺めるという意味で、挑戦してみる価値があるかも知れません。
「本稿の目的」
本稿の目的は、よく知っているはずのことが、あまり一般的に考えられていないことを知り、考える楽しさを味わうことです。日常見ているはずの現象を注意深く考察する訓練と考えてください。
本 文 目 次
1.はじめに
2.速度、加速度、力
3.向心力
4.波の速度
5.おわりに
著者 坂田 明治
第90話 ひもの波の話
1.はじめに
今回は、波の速度について考えましょう。なわとびのひもなどがあれば簡単に実験できます。片方の端をどこかに縛るか、誰かに持ってもらって、波を作り、波の到達時間を計ります。実験結果と、以下の理論的計算結果を比べてみましょう。

どのような波を扱うかというと、「ひもの波」です。まず、図1のように、2点をひもで結びます。そのとき、普通は、図1のように垂れ(たれ)下がった曲線になります。これは懸垂線(けんすいせん)という曲線で、張力が場所によって異なります。そうなってくると、取り扱いが非常にやっかいなので、重力を無視する(無重力)とか、水平にピンと張った場合とか、都合のいい条件を入れます。

さて、図3のようにA点を上下に一回だけ振ると、図4ような波が発生し、A点からB点へ伝わります。

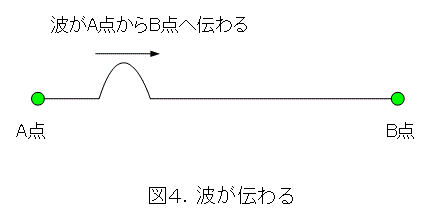
この波の速度は、物理の教科書など、色々なものに書かれています。しかし、波動方程式を使わないで求めるのは結構面倒です。では、もっと別なことを考えましょう。

今度は、A点を図5のように1回転させます。すると、図6のような円形の波が発生してA点からB点へ伝わります。
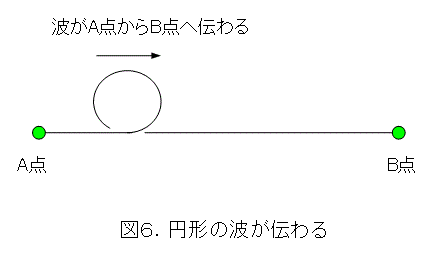
なんか、かえって難しくなっているような気がするかも知れません。こんな波でも波動方程式を使っていいのかと疑問を持つ人もいるでしょう(自分で考えよう)。ですが、こういう、あまり一般的でなさそうな問題を考えるのは楽しいですよ。
2.速度、加速度、力
まあ、のんびりやりましょう。
まずは、速度の話からです。端的に言って、速度というのは位置の変化です。簡単のため、直線上で考えましょう。以下、都合のいいように、色々仮定されているとします。
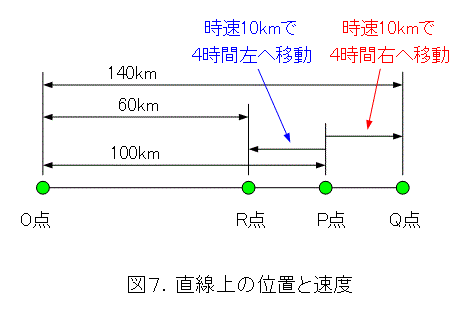
O点を基準(この点のことを原点と言います)として、右へ100kmの所にP点があったとします。そして、P点がQ点(O点から右に140km )に移ったときを考えます。位置の変化になりますが、このままでは速度というには都合が悪いでしょう。P点がQ点に移るのに、瞬間移動したのか、1時間かけて移動したのか、はたまた1億年かけて移動したのかが解りません。観測者にとっては迷惑千万です。いったい、いつまで観測すればいいのでしょうか。
そうなってくると、経過時間も考えなければなりません。こうして、速度の表現は、「位置の変化と時間」とするのがよさそうです。この場合は、「右へ40km移動するのに4時間」となります。4時間で40km移動していますので、1時間当たりに換算すると、40km/4 時間で 10km/h (10km/時 )です。右へ移動していますので、「右へ10km/h で移動」と書くのがよろしいかと。
更に、経過時間を入れて、「右へ10km/h で4時間移動」を考えると、
10km/h × 4h = 40km (10km/時 × 4時間 = 40km )
ですから、「右へ10km/h で4時間移動」で「右へ40km移動」となります。丁度、図1で P点がQ点へ移動したことを表しています。
ここで、重要なのが、「右へ」という方向です。これを「左へ」とすると、図1で P点はR点へ移動してしまいます。
ここまでくると、「右へ」を「+」で表し、「左へ」を「−」で表すと都合よくなるのが見えてきます。慣例にしたがって、「+」を書かないようにすれば、「右へ10km/h で移動」は「10km/h」、「左へ10km/h で移動」は「−10km/h」と簡単に表せるでしょう。
P点、Q点、R点の位置関係から、速度は、「位置の変化をかかった時間で割ったもの」と表現するのがよさそうです。もっと簡略化して、「時間に対する位置の変化率」と呼びましょう。図7をよくみれば、位置の変化は「右」(「+」)か「左」(「−」)ですから、速度には方向のあることが解ります。
そして、 Q点の位置は、100km+10km/h × 4h = 140kmと計算されます。同様に、 R点の位置は100km−10km/h × 4h = 60kmと計算され、いずれの場合も、速度と時間から位置が計算できます。
今度は平面で考えますが、空間の場合も同様です。
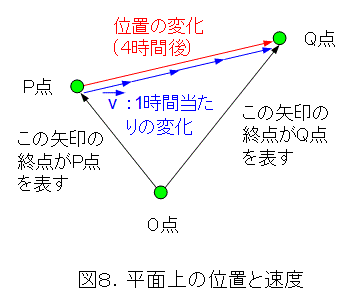
やはり、O点を基準(原点)として、4時間でP点がQ点へ移動したとします。位置の変化は式(1)で示されます。

やってることは図7と全く同じです。しかし、平面上の移動は、直線上の移動のように右左だけでは表せませんので、位置の変化は矢印で表すことになります。したがって、この変化は有向線分であり、ベクトルとなります。
一方で、時間はスカラー(スカラーとは1次元的な量)と呼ばれています。そして、1時間当たりの変化は式(2)で示されます。ベクトルが右から割られることを嫌う人もいますが、ここでは気にしないで進めます。この方が図7の説明と合っていますね。
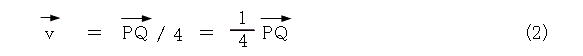
ここで、どうでもいい話ですが、ベクトルのことをベクターとか、ベクタ、ベクトールと呼ぶ人もいます。まっ、人それぞれです。スカラーのことをスカラ(防御力アップの呪文ではありません。念のため)と呼ぶ人もいます。スカラーと呼ぶのであれば、ベクターと呼ぶのが合っていると思います。スカラなら、ベクタですよね。スカラーとベクトルではなんか合わないような。
図7の説明と同様に、速度は「時間に対する位置の変化率」です。式(2)は速度になり、明らかにベクトルですから、速度には方向性があります。
また、図7の説明と同様に、式(3)、式(4)から、 Q点の位置が計算できます。

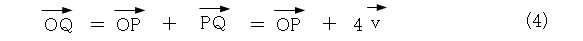
更に、矢印として表現されたベクトルの長さを、「絶対値」とか「ノルム」と呼びます。特に、速度の絶対値(速度を表す矢印の長さ)のことを「速さ」(スピード)と呼びます。図7の説明のところでは、右左または、+−を取った10km/hが速さ(スピード)となります。
平面(空間)で、速度はベクトルですから、方向と速さで表さねばなりません。ですから、北東へ向かって20km/hなどと表します。台風の予報などでよく見かけると思います。km/hのほかに、m/s (m/秒 )もよく使います。 m/sの代わりに、 m/secと書くこともあります。 m/min (m/分 )も使います。混同を避けるため、「分」はmではなくminを使っています。mではメートルと区別がつきませんね。
次に、加速度について考えましょう。加速度というと、車の加速を思い出しますね。たとえば、「俺っちの車は(軽だけど)、スポーツカータイプだから(軽だってば)、抜群の加速性能だ(だから軽だってば)。見よ。この加速度(だから軽なんだってば)」。こういう奴に限って、ほかの車を「なにとろとろ走ってんだよ。亀の方がよっぽど速いぞ」と言う。こんなイメージでしょうか。
車が走るというのは、進行方向と速さ(スピード)をもって移動することです。たとえば、北に向かって60km/hで走ることなど。車が走るのを、速度で表しているということが一目瞭然(いちもくりょうぜん)ですね。そして、加速によって、速さが速くなるので、速度を変化させています。ということから、加速度は速度の変化と考えてよさそうです。ここでも、経過時間を考えなければ都合がよくありません。なんか、速度のときと同じですね。
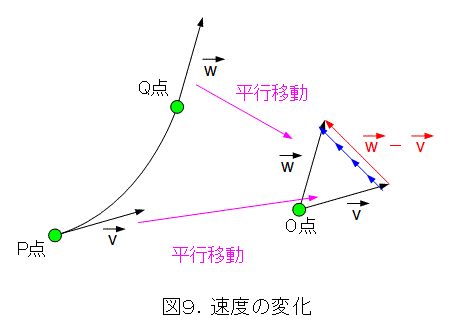
図9はP点での速度の矢印と、Q点での速度の矢印をO点まで平行移動したものです。こうすると、位置に対する速度と、速度に対する加速度とは同じようになります(図8参照)。してみると、加速度は、「時間に対する速度の変化率」と考えるのがよろしいでしょう。ここまでくると、速度の説明のところにあった原点の意味が明らかになります。加速度の説明との対称性を際立たせるためですね(同じだと言って、詳しい説明を省略する手抜きともいう)。
加速度の大きさは、速度の変化を時間で割っていますので、m/s/s (m/秒/秒)などとなります。うっとうしいので、分数の計算をして、m/s2 (m/秒2 )と書きます。ここで、読み方ですが、 x m/s2 を「毎秒毎秒 x m 」と読ませているみたいで、これではなんか解りにくいと思いませんか。「毎秒 x m/s の変化」と読んだ方がいいような。

さて、図9のように曲線状に移動する場合を考えると、時々刻々、位置と速度が変化しています。この場合、ごく短い時間で考えて、それぞれ、時間に対する位置の変化率と速度の変化率を考えなければなりません。これは、微分を考えることになりますので、位置を時間で微分したものが速度、速度を時間で微分したものが加速度となります。ま、あまり気にしないで進みましょう。
最後は力について考えましょう。日常的に力を感じるのは、ものを押したり引いたりするときです。
力をかけると、止まっていたものが動き出したり、動いているものは、動いている方向が変わったり、速くなったり、遅くなったりします。この現象をよく考えてみましょう。止まっているものが動き出すということは、速度が0から変化することです。動いている方向が変わるということも、速度が変化することですね。速くなったり、遅くなったりすることも速度の変化です。
いままで書いてきたことから、加速度が加わったことと同じ現象ですね。すると、力は加速度と同質のものと考えてよさそうです。もう少し考えましょう。重いものを押したときと、軽いものを押したときでは、軽いものの方が小さい力で動き出します。色々な実験の結果から、重さと加速度と力の関係が解りました。重さを用いるとうっとうしくなりますので、「質量」を用いて、

となります(これを力の定義だと思った方がいいです)。ここで、F は力(ベクトル)、m は質量(スカラー)、a は加速度(ベクトル)です。色々とうっとうしくなるので、以降、ベクトル記法はやめます。
式(6)を運動方程式と呼びます。式(6)が「運動の第2法則(運動の法則)」です。ほかに、「運動の第1法則(慣性の法則)」、「運動の第3法則(作用反作用の法則)」があります。これらは、出発点となる法則で他から導けるものではありません(同等なものを仮定すれば導けますが、それでは堂々巡りになるだけです)。
この際、色々とうるさい制約は無視します。
今度は、力の単位について考えましょう。なぜか、質量を記載するのにkg (キログラム)をよく用いますので、式(6)から、力の大きさは、kg m/s2 と書きます。ここで、読み方ですが、 x kg m/s2 を「毎秒毎秒1kg当り x m 」と読ませているみたいで、やっぱり、なんか解りにくいと思いませんか。ここでも、「毎秒 1kg当り x m/s の変化」と読んだ方がいいような。
また、kg m/s2 のことをN (ニュートン)と書きます。上の段落の例では、x N (x ニュートン)となります。この方が、記法や読み方は簡単ですが、上の段落で書いた力の単位も覚えておきましょう。
3.向心力
いよいよ、お楽しみの向心力です。実際に向心力を求めてみましょう。
まず、角度の単位から見直します。通常使っている「度数法」は、1年が、大体360日だったので、円を360等分したものだそうです。調べてないので、この話が本当かどうかは知りません。しかし、ここから先の話では、「度数法」だと、係数がやたらと出てきて面倒になります(これを「π の逆襲」と呼びます)。そこで、もっと理論的な「弧度法」を用います。
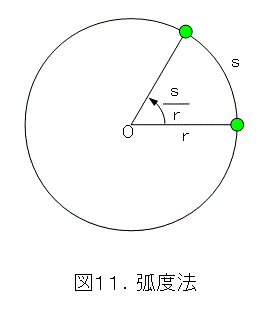
弧度法というのは、弧の長さを半径で割ったものです。図11では、弧の長さを s 、半径を r としています。弧に対応する角度は s/r となります。長さを長さで割っていますので、無単位ですが、それでは解りにくくなるときは「ラジアン」という単位を付けて記載します。図11で、角度は、s/r ラジアンです。逆に、角度θが与えられれば、弧の長さはrθ となります。ここで、直角はπ/2 ラジアンとなります(後で使う)。
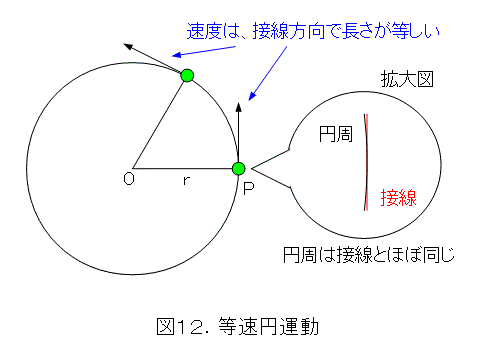
中心O半径 r の円周上をPが反時計回り(時計の針と逆回り)に等速円運動(どこでも速さが同じということ)をしているとします。図12のように、Pのごく近くを拡大すると、円周と接線はほぼ同じになります。したがって、接線方向が速度の方向となります。これから、速度は、図12のようになります。また、接点では、接線と中心方向は垂直です。
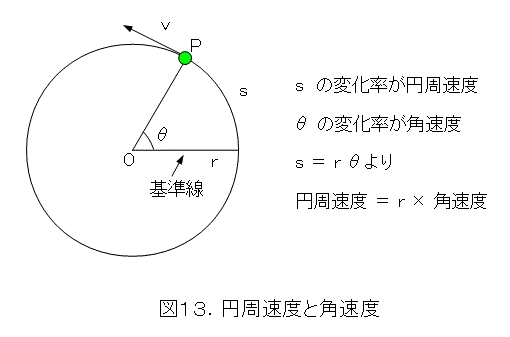
次に、円周速度と角速度について考えましょう。まず、弧度法を使っていますので、弧長と角度はほぼ同じものです(比例するという意味)。すると、図12のように、円周速度と角速度とはほぼ同じものになります(比例するという意味)。ここで、円周速度と角速度はスカラーと考えましょう(速度なんて書いてあるけど)。
等速円運動では、円周速度が一定ですから、角速度も一定となります。角速度が一定ということは、角度の変化率が一定です。変化率というのは、時間に対する変化率のことでした。つまり、時間に対して比例するということですね(比例定数が変化率)。
これから、
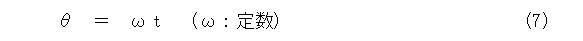
と書けます。
ここから先、かなり大胆な近似計算を行いますので覚悟してください。記号を準備します。変数の前にd と付けたら、その変数は微小(0に近いということ)であることとします。たとえば、微小な時間を表すのはdt です。微小な時間に対しては、角度も微小にしか変化しませんので、

となります。
角度が微小であれば、弧長も微小ですので、
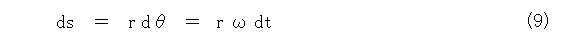
が出てきます。
円周速度をv とすれば、v は微小な弧長の、微小な時間に対する変化率ですから、

です。
もうひとつ準備をしましょう。
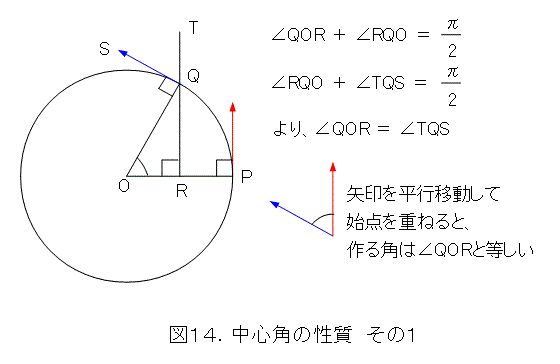
等速円運動をしているとき、円の2点間の速度の作る角に関しては、図14のような関係があります。
いよいよ、向心力を求めるときがきました。
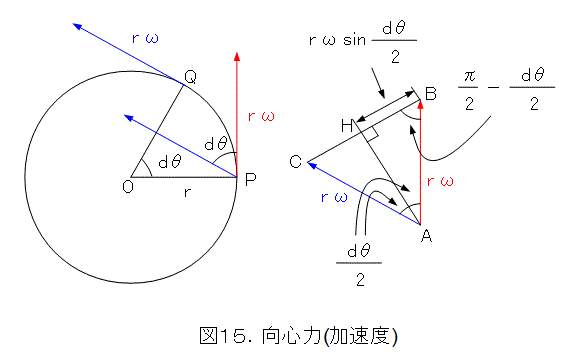
図15から、
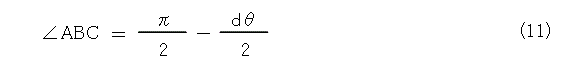
ですが、dθ は微小なので無視して、式(11)の右辺はπ/2 とみなせます。これは、BCがABに垂直であること。つまり、速度の変化である加速度は、接線方向と垂直です。P点にかかる加速度なので、結局、中心へ向いていることを示しています。質量を掛けても方向は変わりませんので、本当に向心力となっていることが解ります。
次に大きさを求めましょう。まず、dθ が微小なので、dθ/2 も微小です。これから、

とみなします。
こうすると、v の微小変化dv は、図15によって以下のように求まります。
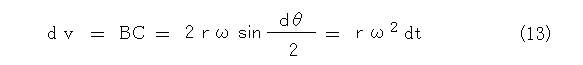
ここまで来ると向心力が求まります。運動方程式(式(6))で、Fを向心力(の大きさ)、m を等速円運動しているものの質量、a を加速度(の大きさ)として代入するだけです。a = dv/dt であることに注意して、

と求まります。
4.波の速度
今度は波の速度を求めましょう。
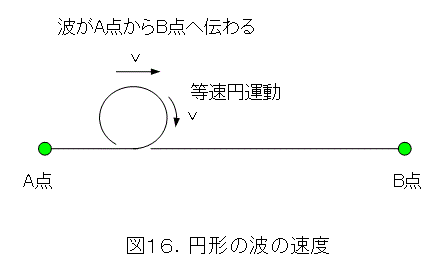
円形の波は、A点からB点へ向かっていますので、波の速さだけが問題となります。回転速度が、波の進行速度になりますので、回転速度を求めればよいことになります(回転方向が今までと逆だけど)。これ、レールの上を転がる車輪と同じですね。なお、ここでも、波の発生で張力が変わらないとか、都合のいいような仮定が続きます。
また、いくつか準備します。最初は、「張力」です。
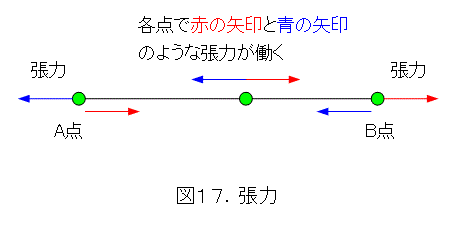
張力は、ひもを引っ張っている力です。ひも自体は動かず、重力を無視しているので、図17のように、どの点でも互いに逆向きの張力がかかって釣り合っています。
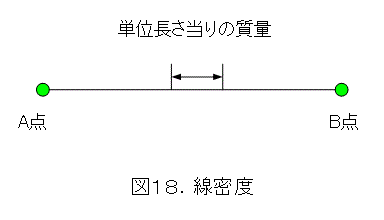
次は「線密度」です。これは、図18のように、単位長当りのひもの質量です。1メートル当り何キログラムという量です(m を質量としたため、うまく単位系が書けなくなってしまった)。ひもは、線密度が一様(どこでも同じということ)と仮定します。すると、波の速度は一定と考えられますので、円周速度は一定になります。ひもの線密度をρとし、せっかくなので、今までに使った記号を流用します。
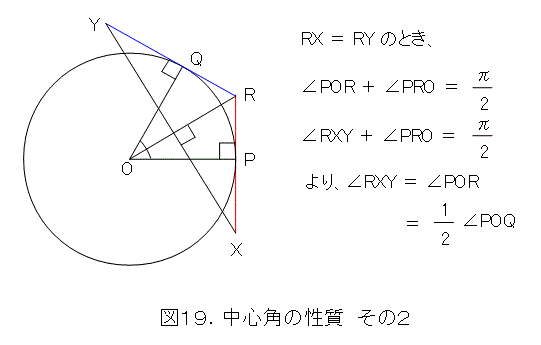
円の性質も必要です。円の外の点から、円周に接線を2本引きます。このとき、図19にある性質が成り立ちます。
以下、面倒なので、張力はスカラーとベクトルを混同して扱います。色違いでベクトルとしては違っており、スカラーとしては同じとして扱います。
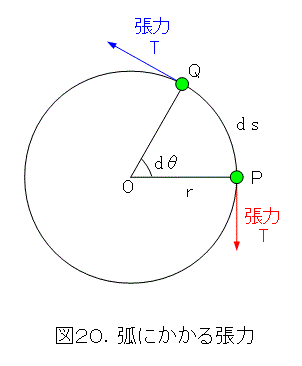
さて、図20のように、円周上に微小な弧ds を取ります。また、これに対する微小な角度をdθ とします。ds = r dθ ですので、質量に関して、

が成り立ちます。
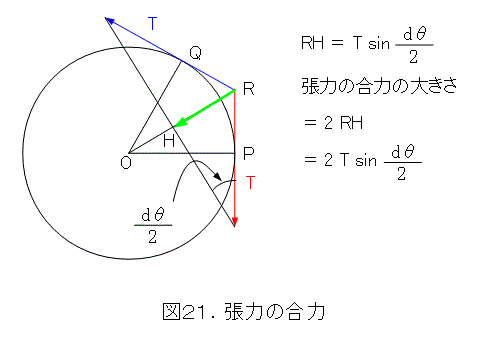
図21のように、微小弧にかかっている張力を平行移動し、始点を重ね合わせると、張力の合力が求まります。
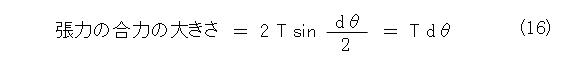
一方で、式(14)から向心力の大きさが求まっていますので、式(14)に式(15)を代入して(式(10)も代入)、
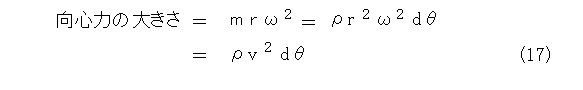
と向心力が求まります。
張力の合力が向心力となりますので、

が成り立ちます。v について解いて、

となり、これが波の伝わる速さです。
この式に見覚えのある人も多いと思います。普通の教科書に図4の波の伝播速度として書いてありましたよね。
5.おわりに
波というと、サインカーブを連想する人も多いかと思います。また、波は円と密接な関係にあることを知っている人も多いでしょう。
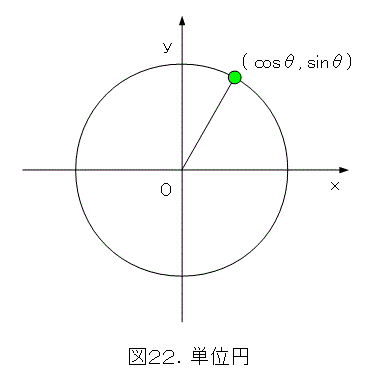
単位円周上の点が回転すれば、x 座標やy 座標から、よく知っている波としてサインカーブが出てきます。しかし、円と波が密接な関係にあるなら、「なぜ、波の形として円が出てこないのか」と疑問を持った人もいるかも知れません。この疑問とは、池に石を放り込んで円形に拡がっていく波のことではありません。波そのものが円形になるということです。
本稿の冒頭で見たように、円形の波は簡単に作れます。図3と図5を見比べれば解るように、波の進行方向を逆転しています。つまり、通常の波を裏返すと円になるということです。なるほど、ものごとには表と裏があり、裏が本来の姿を現すということでしょうか。
その昔、まだテレビゲームもなかった時代、遊び道具は限られていました。なわとびのひもなども遊び道具でした。よく、円形の波を作って、それを絡めるという遊びをしたものです。限られた道具を工夫して使っていましたね。懐かしいと思う方も多いかも知れません。
このような遊びをしていた子供が、高校で波を習うと、波はサインカーブと毒され、円形の波があることをすっかり忘れてしまうのはなぜでしょうか。不思議ですね。
完
平成25年11月27日
著作者 坂田 明治(あきはる)
|