|
第91話
立方体の倍積の作図
|

「主な対象読者」
今回は作図に興味を持つ人が対象です。作図には、理論と、実際の作図があり、理論を楽しむ他に、作図用の器具を製作する楽しさもあります。工作の好きな人は、実際に作図用の器具を製作してみるのも面白いでしょう。
本 文 目 次
1.はじめに
2.作図用の器具
3.作図できる理由
4.実際の作図
5.おわりに
著者 坂田 明治
第91話 立方体の倍積の作図
1.はじめに
定規とコンパスだけで作図できないものは多々あります。角の三等分はできませんし、正7角形の作図もできません。このことは、「第80話 不可能にまつわる話 5.角の三等分」、「第86話 正7角形の作図問題」に出ています。このように「あれもこれもできません」というのばかりでは面白くありません。
しかし、同時に、「第80話 不可能にまつわる話 5.角の三等分」でアルキメデスの方法によって角の三等分をしていました。これは定規の使い方を、与えられた2点を結ぶ直線を引くというだけの機能から開放した作図でした。
また、「第88話 電車の速さと車輪の速さ 〜寝心地の話続編〜」でサイクロイドを作図する器具を作りました。より前の作品「第6話 鏡の国の光子さん その二」では、だ円を作図しています(器具といえるほどのものではありませんが)。
以上の例から、定規とコンパス以外の器具を使えば、作図できる図形の種類が増えると予想されます。そこで今回は、立方体の倍積問題の作図を考えましょう。なお、立方体の倍積問題というのは、与えられた立方体の辺から、体積を2倍にする立方体の辺を作図するという問題です。
2.作図用の器具
まず、立方体の倍積問題を簡単に書くと、体積1の立方体(辺の長さは1)に対して、体積2の立方体の辺を作図するということです。これは、2の立方根(3乗根)の作図です。しかし、2の立方根は定規とコンパスで作図できません。(「第80話 不可能にまつわる話 5.角の三等分」に詳しい説明があります。また、以下、掛け算、割り算の作図を使いますが、これらの方法についても詳しく書いています)
そこで、定規とコンパス以外の器具の登場となります。
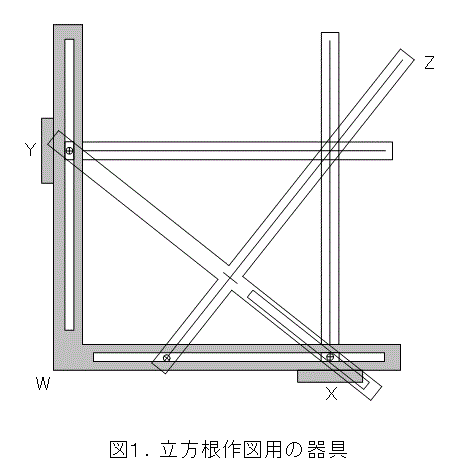
図1は立方根の作図用器具です。いかにも器具らしいですね。
使い方を説明します。L字型をしているWに対して、Xは横方向にスライド、Yは縦方向にスライドします。そして、十字型であるZがスライドして、図1の右上の方にあるように、3本の直線が1点で交わったときに立方根ができます。どこに立方根ができるかは第3章で詳しく扱うことにします。
この動きは少し複雑なので、個々の構成要素を詳しく見て行きましょう。
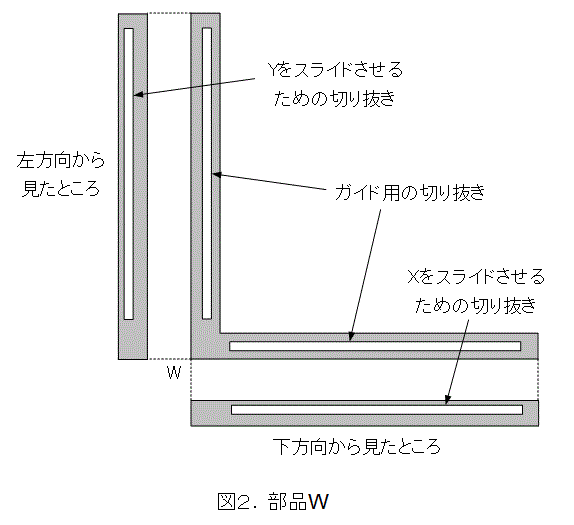
最初はWです。上から見ると、L字型になっており直交しています。すなわち、横の腕と縦の腕が直角です。これは、図に描いていませんが、L字型のそれぞれの中心線が直角になっていることです。そしてガイド用の切抜きがあり、中心線に沿っています。
次に、側面から見てみましょう。画面の下方向から見ると、Xを差し込んでスライドさせるための切抜きがあります。もちろん、これはL字型の側面の中心線に平行です。画面の左方向から見た場合も同様です。ただし、XとYを差し込んだときに衝突しないように、それぞれの切抜きの位置はずれています。
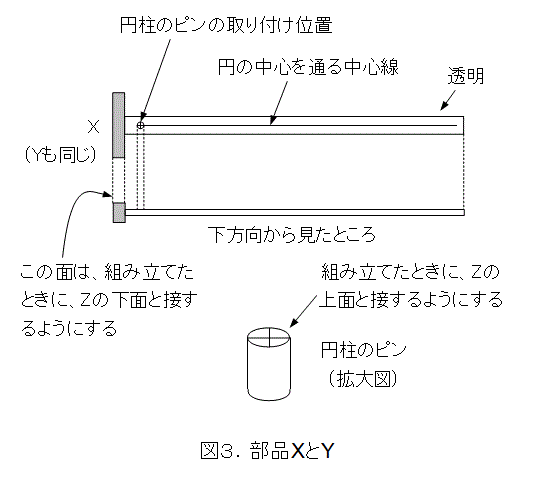
XとYはWの側面から差し込むT定規みたいなものです。図3で、透明な部分の定規には中心線を描いておきます。更に、XとYをWの側面から差し込んだときに、円柱のピンを、ガイド用の切抜きに合わせて取り付けます。この円柱の上面には、直行する直径を描き、中心が解るようにしておきます。また、取り付けたときに、透明な部分の定規の中心線と、円柱の直径を直線的に接続し、この中心線は、それぞれ取り付けたZの腕の中心線と直交するようにします。
なお、取り付けたときの円柱のピンの長さは、円柱の上面とZの上面が接するようにします。この理由は第3章で説明します。
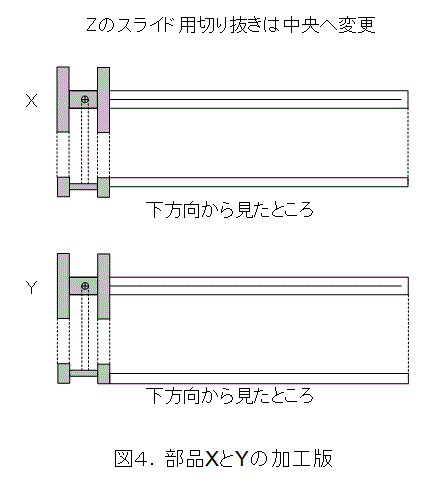
図3の作りでは不安定なので、図4のように改良することもできます。これは、図1の器具を置く台と、X 、Y 、Zがそれぞれ接するようにしたものです。他にも色々と改良の余地があります。
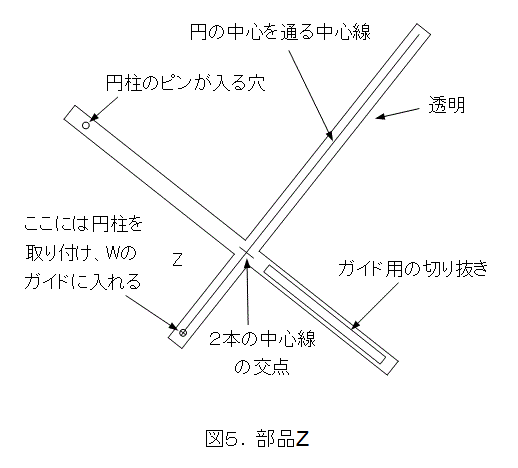
Zは十字型の定規です。もちろんこの十字は直交しています。
以上を組み立てれば、図1の器具となりますが、改良の余地が多々あります。第3章を読んでから、もっと作図に適したように改良して作るとよいでしょう。
3.作図できる理由
この章では、作図用の器具を数学的に模式化し、どこに立方根ができるかを説明します。
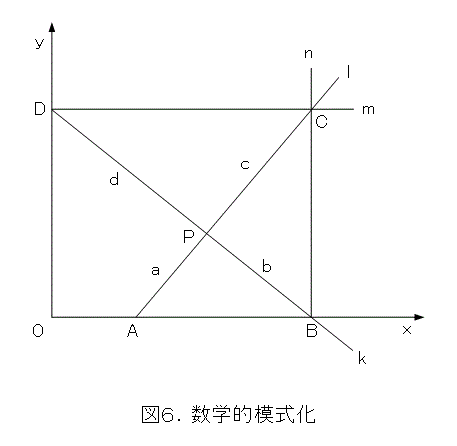
図6は、Wの中心線をそれぞれ x 軸と y 軸、X 、Yの中心線をそれぞれ直線 m と n 、Zの直交する中心線を k と l としたものです。また、a 、b 、c 、d は長さなので全て正とします。
さて、ここで重要な事実があります。d > a であれば、必ず(どっかの国の国民の生活水準と同じように) k を右肩下がりにできます(理由は自分で考えましょう)。その結果、k は x 軸の正の部分で交差します。つまり、図6に描いてあるようにできるということです。これはまた、図1の器具が作れるということです。
最初に図を見てしまったから、当たり前と思うかも知れませんが、その図が本当に描けるものであるかと考えることは重要です。特に、今回は「作図」がテーマになっていますので尚更です。
では、悪い例を出しましょう。「全ての三角形は二等辺三角形」というパラドックスがあります。
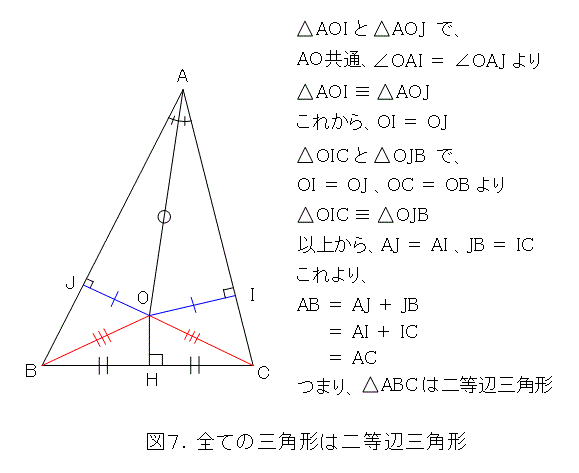
勝手な三角形を書いて、最も悪い原因(定規とコンパスで作図できます)と、その頂角に対応する辺の垂直二等分線(定規とコンパスで作図できます)の交点を取り、そこから2辺へ垂線を下します(定規とコンパスで作図できます)。図7にあるように、直角三角形が何個かできます。直角三角形の合同条件は簡単なので、図7に書かれているようにして、「全ての三角形は二等辺三角形」を示せます。
さて、何が悪いのでしょう。引っ掛かった人の最も悪い原因は、「自分で作図して確かめないこと」です。人が描いたものをそのまんま使っているのが原因です。定規とコンパスを用いて、自分で作図すればたちどころに解決しますので、実際にやってみましょう。
ということで、本当に描ける図であるかどうか確かめることには意味があります。
図6へ戻りましょう。直角三角形が何個ができています。直角三角形の相似条件は簡単なので、すぐに、
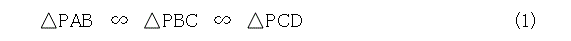
が解ります。相似比に注目すると、

となります。これから、


が出てきます。式(3)の両辺を2乗すると、

式(4)と式(5)を掛け合わせて、

これから、

ここで、d = 2 a とすれば、

したがって、

特に、a = 1 とすれば、

となって2の立方根が作図できます。
a = 1 としなくても、割り算は定規とコンパスで作図できるので、a を適当に大きな数にしておいて、もうひと手間かけても作図できますね。
また、d = f a とすれば、

となります。d > a でしたので、1より大きな作図可能な数の立方根は作図できます。0 、1 の立方根は自分自身なので作図不要ですし、0 と 1 の間の数は、逆数を取って作図し、その逆数を取ればいいので立方根が作図できます。なお、逆数は、割り算が定規とコンパスで作図できることから問題ありませんね。
以上から、図1の器具を使えば、作図可能な数の立方根は作図可能であることが解ります。また、図1の器具のどこに作図されるかも解りましたね。器具の下ではなく、器具の上に作図結果ができてしまいます。ですから、円柱のピンの上面とZの上面を接するようにする必要があったのです。穴を開けるなどして改良し、器具の下に作図結果を描けるようにした方がよいかも知れません。
他にも問題点が浮き彫りになっています。作図する数に対応してZを用意しなくてはなりません。いちいち作るのも面倒なので、もっと簡単にやる方法を考えましょう。
4.実際の作図
まず最初に、作図には、理論と実際の作図の両面があります。理論的に考えられる直線や円などは、現実にある定規やコンパスでは作図できません。大きさをもたない点や、幅のない直線などは描きようがないでしょう。更に、定規やコンパスなどは、微妙にゆがみやたわみがあったりします。その点でも完全な作図にはなっていません。つまり、実際の作図は、近似的なものであるということです。より完全なものに近づけるには、精度を上げる必要があります。これは際限のない努力で、精度を上げ、誤差の範囲を抑えるのは非常な努力を要します。それでもやる必要がある限り挑戦は続きます。
本稿では、精度を考えていませんから、その辺は適当にやっています。適当ついでに開き直って、更に手抜きをし、もっと簡単に立方根を作図する方法を考えてみましょう。
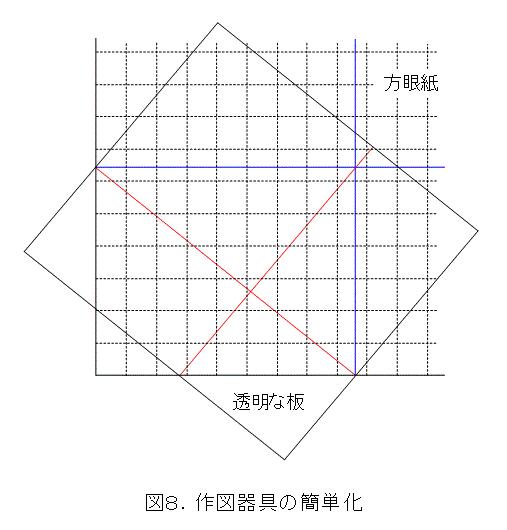
作図器具の、各構成要素をもっと簡単にならないか考えてみると、方眼紙と透明な下敷きなどの板があればできそうです。方眼紙にWに相当する部分の線を引いておきます。そして、透明な板に直交する直線を引いておきます。あとは透明な板を動かし、図8のようにします。方眼紙の縦横の線が、必要な部分に丁度一致することはまれなので、その辺は目分量でやります。そのときに、「作図には誤差があるので、これは許容範囲だ」と自分を言い聞かせます。
これで、立方根の作図ができました。どこにできたかは第3章で示されています。もう少し工夫すれば、図8の青い直線を取り扱えます。しかし、3直線が1点で交わっていることの確認は目視ですので、精度はあまり上がらないでしょう。
5.おわりに
古代ギリシア人達は、定規とコンパスでの作図を考えるとともに、色々な作図用器具を考案して作図を行っていました。定規とコンパス以外の器具を用いれば、当然、作図可能な範囲は広がります。普通はそう考えますが、話はそう簡単ではありません。その器具を用いたことによって作図でき、しかも、定規とコンパスでは作図できないことを示さなければならないからです。
それはそうと、「第86話 正7角形の作図問題」のアクセスログを調べてみると、「正七角形、簡単な作図」という複合キーワード検索で入ってこられる方が多く見受けられます。何を意図してこのキーワード検索をしているのかは本人しか知りませんが、ある程度推察はできます。
おそらく、「正五角形の作図」を学んだ人が、次は「正七角形の作図」と考えたのでしょう(正六角形の作図は簡単)。ここでふと、二つほど疑問がわきます。一つは、先生が授業で、正五角形の作図を教えた後、正七角形は定規とコンパスで作図できないと教えていないのでしょうか。
何か理由があるのでしょうか。最悪、先生が作図不能であることを理解してないために教えられないということもありえます。そうだとすると問題です。先生の質に関わり、勉強嫌いの原因にもなりかねません。
もっとも、自分で勉強して正五角形の作図を学び、次は正七角形の作図を学ぼうとしている人もいるかも知れません。かつて、家が貧乏で、独学だったため、人付き合いが悪く、出世し損ねた人もいましたから。
もう一つの疑問点は「簡単な」ということです。何でもネットで探せば簡単な方法が手に入るとでも思っているのでしょうか。これは重大な問題です。どうすればよいかは、今後の検討課題としましょう。(政治家みたいな終わり方だな)
完
平成26年3月8日
著作者 坂田 明治(あきはる)
|