|
第94話
重心の位置
|

「本稿の目的」
本稿の目的は、式の導入実験にあります。これは、導入の手間を調べるためであり、読者を想定しておりません。 しかし、それではあまりにも無体な所業なので、重心を求めることについて記載しています。著者が過去に行ったときに比べ、色々と道具が用意されているため、多少は実験しやすくなっていると期待されます。
本 文 目 次
1.はじめに
2.質点系の重心
3.物体の重心
5.おわりに
著者 坂田 明治
第94話 重心の位置
1.はじめに
今回は、読者を対象としていません。
以前より、記号がまともに使えないため、式が入らないという問題がありました。記号が環境に依存するなんて、まったくなに考えてるんだ。それに、小さすぎる、肝心なものが用意されてない。困った、困った、なんとかしてほしい、と文句言ってても話は進みません。
そこで、本稿は式を入れる手間の実験用に作ったものです。ほら、理科好き子供の広場のトップページにも「知的好奇心に基づく実験場」と書いてありますし。まあ、極端なことをいうと、積分記号の取り扱い実験が目的です。他の記号はおいおい導入を試みましょう。
話題はなんでもよかったので、重心の位置を求めることにしました。2章、3章が個人的実験の章です。重心の位置測定方法を知りたい人は、4章へ飛んだ方がよいと思います。一応、実験方法が書いてあります(一応ね)。
2.質点系の重心
この章と、次の章を書くに当たって、ベクトル記号(有向線分記号)は用いません。x i とか x はベクトルです。一々太らせたり、上に矢印を付けたりしません。こういう使い方の方が一般的です。しかし、どうしても気分が悪いという人は、x i や x は x 座標と思いましょう。他に y 座標と z 座標があり、手抜きで x 座標しか書いてないと思っても差し支えありません。
まずは質点系で考えます。
最初は、質点が1個だけの場合です。
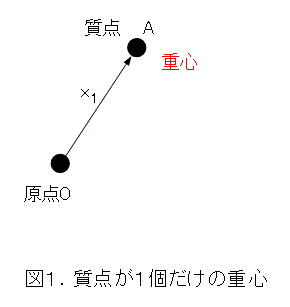
このとき、質点の重心は、質点の位置になります。当然ですね。

あえて重心の位置を式で書けば、式(1)のようになります。
次に、質点が2個の場合を考えましょう。質点1と質点2で、質量が等しいとします。
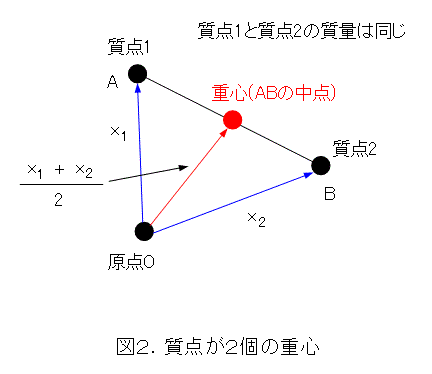
このとき、重心は、質点1と質点2の位置の中点となります。感覚的に考えてもそうですね。これさえ解れば、物体の重心まで求められます。以下、順を追って求めて行きましょう。
中点というのは、位置の平均でしたね。
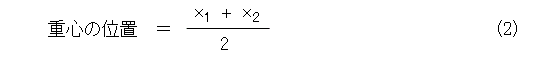
式で書けば、式(2)となります。確かに位置の平均(より詳しく書くと、「相加平均」)になっていますね。
重心というのは、それぞれの質点からの影響が拮抗(きっこう)(釣り合うということ)する場所ですから、質量が等しい限り位置の平均となります。
したがって、質点が3個で、質量が等しい場合も、以下のようになります。
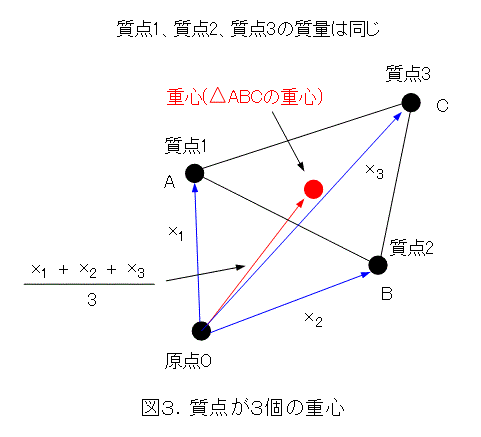
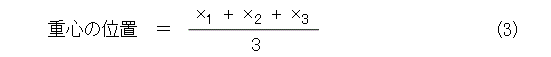
丁度三角形の重心になっていますね。
質点が n 個で、質量が等しい場合も位置の平均ですから、以下のようになります。
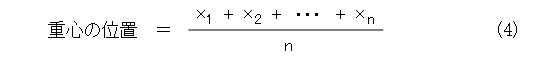
さて、質量が、異なっている場合を考えましょう。質点1が質点2の2倍の質量だったとします。このときは、質点1の所にもう一個質点1が重なっていると考えて、質点が3個の場合に帰着されます。
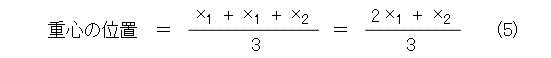
m 1 、m 2 を正の整数として、質点1の質量を m 1 、質点2の質量を m 2 、とすれば、それぞれ、質点が m 1 、m 2 個ずつ重なっていると考えて、式(6)のようになります。
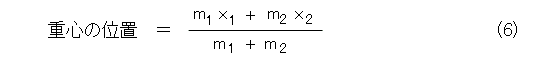
より一般に、質点を n 個とし、それぞれの質量を m 1 、m 2 、・・・ 、m n (これらは正の整数)とすれば、それぞれ、質点が m 1 、m 2 、・・・ 、m n 個ずつ重なっていると考えられるので、式(7)が得られます。
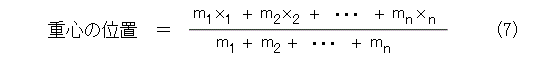
今度は、質量が正の有理数)になる場合を考えましょう。質点1の質量を m 1 = q 1 / p 1 、質点2の質量を m 2 = q 2 / p 2 ( p 1 、p 2 、q 1 、q 2 は正の整数)とします。質点1、質点2に同じ数をかけても重心の位置は変わりませんから(質量が同じなら、重心は位置の平均になることが出発点でした)、それぞれに、 p 1 p 2 をかけます。そうすれば、それぞれの質量は、正の整数になるので、式(8)が求まります。

同様にして、式(7)は質量が正の有理数でも成り立つことが解ります。
分母がうっとうしいので、式(9)のように、全質量で割っておけば、式(10)のように見通しがよくなります。
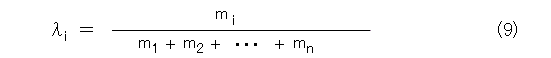
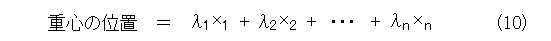
ここで、質点の質量がちょっとしか変わらなければ、重心の位置もちょっとしか変わりません。このことから、式(10)を連続拡大し、正の実数に対して式(10)から重心の位置が求まります。これで質点系の場合は求まりました。
式(10)は、係数が正で、係数の総和が1ですから、線形代数を勉強された方にはなじみの深い式ですね。
3.物体の重心
いよいよ、物体の重心を求めるときがきました。なお、ここで、物体を剛体と考えても差し支えありません(時間を止めて考えているから)。
まず、いつものように、物体を切り刻んで微小部分の集まりとします。
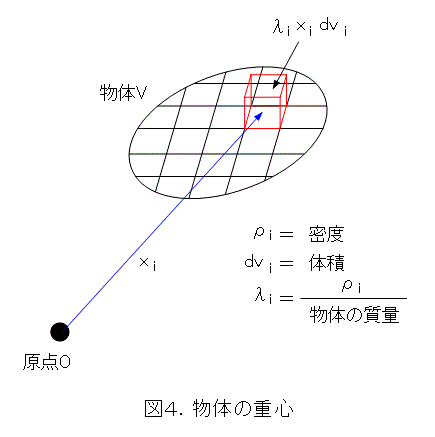
その上で、微小部分を質点で近似します。図4の x i の位置の微小物体で、密度を ρ i とし、体積を dv i とすると、質量は ρ i dv i となります。物体の質量をMとし、 λ i = ρ i / Mとおけば、重心の位置は式(11)で近似できます。
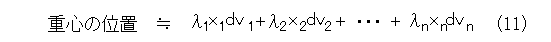
極限移行して、重心の位置は式(12)となります。
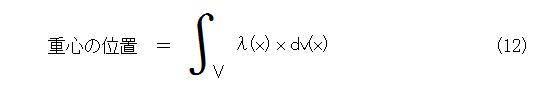
物体の質量は、密度を積分すれば求まるので、式(13)となります。
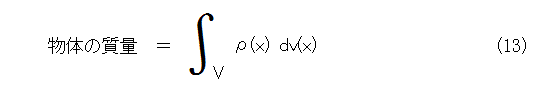
これらから、どうしても式(12)では「いやじゃ」という人は、
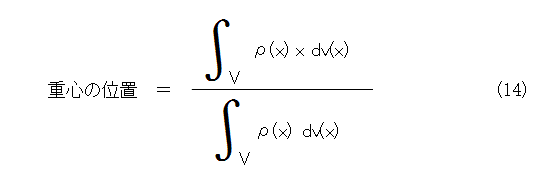
とすればよろしいかと思います。
4.おまけ 物体の重心を求める実験
ここでは、重心を求める実験方法を紹介しましょう。簡単のため、厚紙を切って作った物体を考えます。2次元化していると考えても差し支えありません。
よく、以下のようにすれば物体の重心が求まると書かれています。
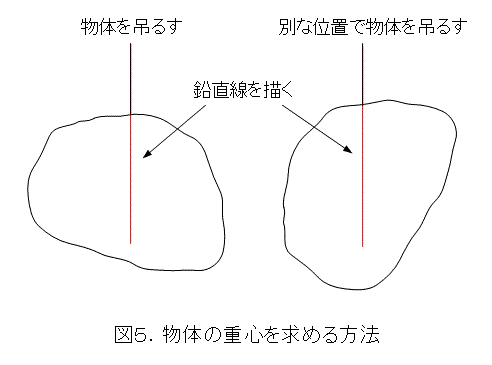
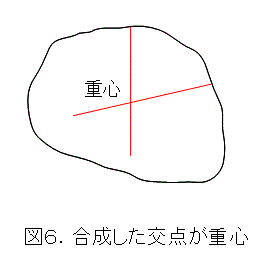
要するに、物体を2箇所で吊るし、鉛直線を描き込み、その交点として重心を求めるというものです。間違いではありませんが、こう書いてる人は、本当に自分で実験したことがあるのか疑問です。
だいたい、よくこんなにも気楽に書けるなと思います。昔、やってみましたが、色々と難しいし、理論的な位置と合わないし、その上求まらないものもありました。
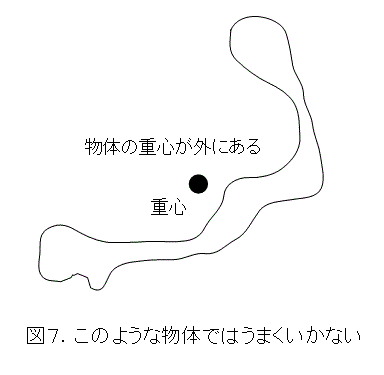
図7のように、重心が物体の外にはみ出している場合は求まりません。正確には、物体には鉛直線がちょびっとしか描けず、物体を板の上に乗せ、そこで鉛直線を延長して求めると、やたらとずれがでてくるということです。
そうでなくとも、色々難しい問題が出てきます。まず、物体をどうやって吊るすのでしょうか。糸を接続しなければなりませんが、これはどうするつもりでしょう。クリップに糸を付け、クリップで物体を挟む(はさむ)のはだめです。物体とクリップが一緒になってしまうため、何を測っているのか解らなくなります。
更に、なんとか吊るしたとしても、物体がふらふら動いたり、糸に合わせて定規を当てようとしても、ずれたりしてうまくいきません。
そこで、実験方法を考えてみました(あくまでも考えただけね)。
まず、実験には重心の解っているものを使いましょう。三角形の重心は作図で求まりますから、厚紙に三角形と重心を作図して、三角形を切り出します。当然ですが、作図による誤差もあります。
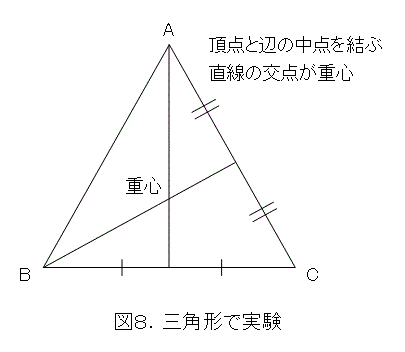
次に、三角形に小さな穴を開けて、ここに黒い糸を通して縛ります。これによる誤差も少しでます。黒い糸はある程度太くしなくてはなりません。写真を撮ったときに見えるようにするためです。
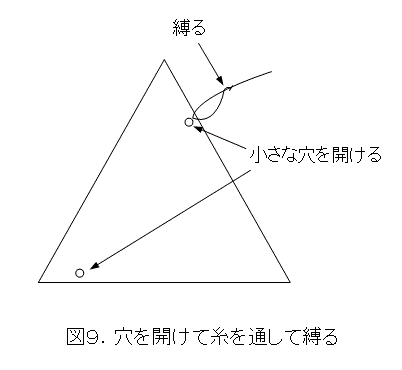
糸を付けるのは一箇所ずつとします。つまり、片方のみ糸を付けて測定し、測定後、その糸は外してから、もう一方に糸を付けて測定するということです。
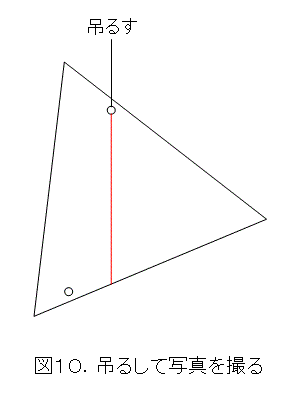
この測定は、どこか白っぽい壁を見つけてスクリーンとして用います。また、デジタルカメラを三脚かなにかで固定します。そして、吊るした三角形は、白い壁に接するようにし、ふらふらさせないで撮影します。当然、もう一方の穴に糸を付けた場合も同じ位置で撮影します。
撮影した2枚のデータはパソコンに取り込み、片方の写真を半透明化します。それから、2枚とも黒い糸に重なる直線を描き込みます。こうしておいて、パソコン上で、半透明化した画像を適当に回転や平行移動させて重ね合わせます。
ちゃんと同じ距離、同じ角度で撮れていないと、うまく重なりません。これは難しいので、この際、多少のずれは誤差として無視しましょう。
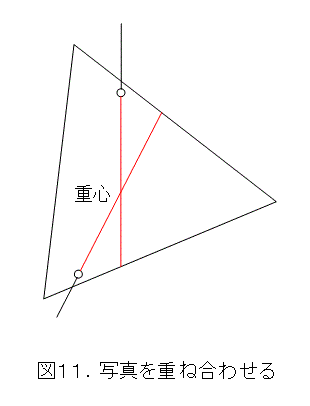
こうやって重心を求めますが、恐らく、最初に作図した三角形の重心とずれていると思います。まあ、測定誤差ということで納得しましょうね。
これでなんとかできると思います。しかし、実験機材とソフトがないため、確認はできていません。
5.おわりに
今回は、式の導入による手間を調べるのが目的でした。その意味では、ある程度なんとかなりそうです。
これで締めくくっても構わないけど、おまけの方でやったことについて書いておきましょう。理論的にはそうなるから、あるいは、やればできそうな感じなので、自分で確かめもせず、こうすればできると他人に教えるのはどうでしょうか。実際にやってみたら、難しいどころかできない。なんてことにもなりかねません。
よく、コピペはいかんと言われていますが、自分で確かめもせずに人に教えるのは、それとあまりかわらない気もします。どうでしょうか。
念のため、注意をしておきます。コピペが全くだめということはありません。引用としてのコピペなら許されています。その際には、引用部分が解るように「」などで囲み、著者と出典を明示します。詳しくは、「論文の引用」で探すのがよろしいかと思います。
完
平成27年2月22日
著作者 坂田 明治(あきはる)
|