|
第97話
制限作図問題 〜正五角形の作図付〜
|

「主な対象読者」
今回は作図に興味を持つ人が対象です。作図には、実際の作図と、その作図の根拠を与える理論とがあります。理論的に作図可能となった場合、その作図可能であることを導き出す推論にしたがって作図をすれば作図できますが、一般的に複雑です。しかし、作図可能であるということから、とにかく作図方法があると保障されます。そこで作図方法を考えれば、簡単な方法が発見できることもあります。作図の好きな人は、作図可能な図形の作図をしてみるのも面白いでしょう。
本 文 目 次
1.はじめに
3.反転
4.コンパスで作図
5.正五角形の作図
6.おわりに
著者 坂田 明治
第97話 制限作図問題 〜正五角形の作図付〜
1.はじめに
今回は、久しぶりに作図問題です。第80話、第86話を読まれた方は、定規とコンパスでは作図に限界のあることが解っていると思います。そして、第91話を読まれた方は、定規とコンパス以外の器具を追加して用いれば、作図可能な範囲が拡大するということを知ったはずです。
それなら、もっと色々な器具を導入してやれば、更に作図可能な範囲は拡大するであろうという考えが自然に浮かびます。当然、色々な器具を導入して、作図可能な範囲を広げるのが今回の目的だと期待されたことでしょう。
そういう期待を裏切り、今回は、器具にもっと制限を加えてみます。具体的には、コンパスだけの作図です。
2.コンパスだけの作図
まず、予想を立てましょう。定規を用いず、コンパスだけで作図をするのだから、当然、定規とコンパスで作図をするよりも、作図できる範囲は狭くなると予想されます。その予想が当たっているかどうかを調べていきましょう。なお、今回は、第80話、第86話のような代数的な取り扱いは出てきません(数体を使いません)。すべて初等幾何の範囲で済みます(しかも円だけ)。
ちょっと考えれば(考えなくても)、定規を使わないのだから、相異なる2点を結ぶ直線の作図はできません。予想は正しかった。
完
このパターンは以前にもやりましたね(第89話)。これでは面白くないので、直線について考え直します。
ユークリッド幾何学(普通の幾何学のこと)では、最初に、
「相異なる2点を通る直線が1本だけ引ける」
というのが公理として出てきます。これ、よく使うし、常識的な範囲ですね。
逆に、直線が先に与えられれば、直線上に相異なる2点を取れます。そして、上の公理によって、その相異なる2点から直線が1本定まります。この直線は、当然、元の直線です。こう考えると、相異なる2点の組と、直線とは同じものとしてよい(同一視)ことになります(苦しい言い訳にしか見えませんが)。
以上、相異なる2点の組があれば、そこに直線が引かれているとみなします。
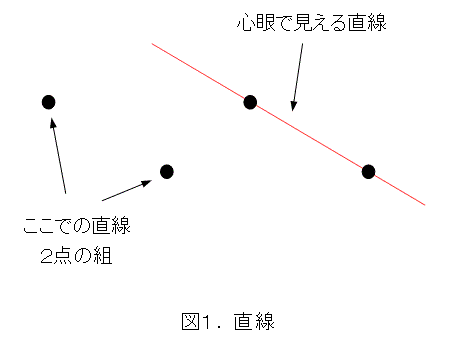
いや、すごいことになりましたね。図1のように、実際には相異なる2点の組を直線としますが、心眼によって、そこに直線が見えるようにしてしまえというのですから(心眼を開眼)。
なお、この「なんとかとみなす」というのは、非常に重要な考え方です。やがて役に立ちます。しっかり身に付けましょう。
これで振り出しに戻りました。定規とコンパスによる作図の範囲と、コンパスだけを使った作図の範囲を考え直しましょう。
定規とコンパスによる作図については、第80話に書きましたが、ここでもう一度出します。
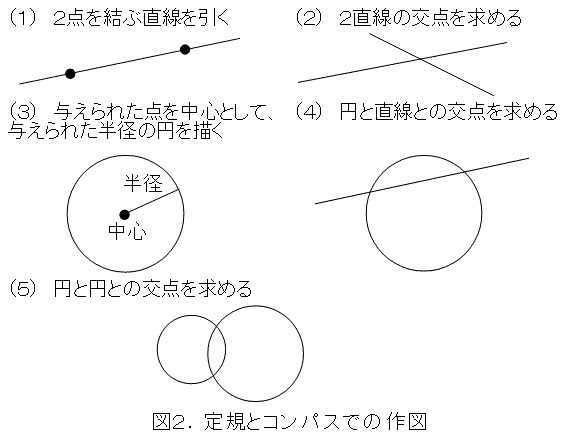
この図2にある一連の手順を有限回組み合わせることが、定規とコンパスで作図するということです。
こうして、図2の手順について、コンパスのみで作図ができるかできないかを調べれば、作図できる範囲について、狭くなっているかどうかが解るようになりました。実際に調べていきましょう。
まず、(1)は、心眼を開眼したのだからできたことになります。(3)と(5)は当然できますね。そうすると、問題なのは、(2)と(4)です。この2つについて、やるべきことは、作図できるなら、作図方法を示し、作図できないなら不可能の証明をすることです。
3.反転
誰でも、コンパスを使った作図として思いつくのは円です。コンパスと円とは切っても切れません。したがって、ある程度、円の性質を知らないと話しになりません。
ここでは、円に関する変換として反転を扱い、その反転の性質を調べます。なお、第63話で反転について少しやっており、その性質を使ってポーセリエの反転器とハートの反転器を扱っています(今回は、第63話に少し内容を追加します)。なお、関数論を学ばれた人なら、反転のことを詳しく知っていると思います。
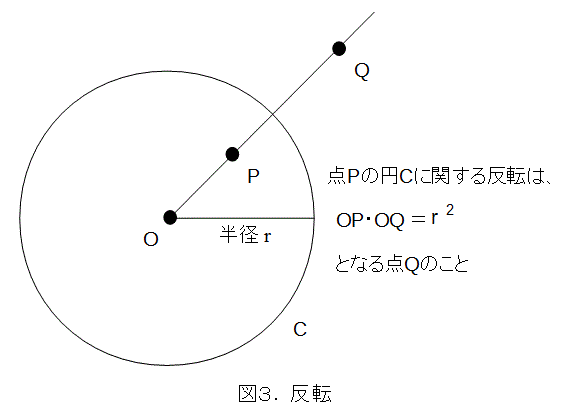
中心Oの円Cに関する反転というのは、図3にあるように、点Pを点Qに変換することです。図3を見れば解りますが、点Qの円Cによる反転は点Pです。つまり、点Pと点Qは円Cに関して互いに反転になっています。つまり、反転の反転は元に戻ります。これから、点Pに対して点Qは逆点、点Qに対して点Pは逆点とも呼びます。
反転の性質として、すぐに解ることは、円周上の点は動かさないことと、円の中と外が入れ代わることです。
ここで、1点だけ問題点が出てきます。円Cの中心Oは反転によってどこへいくのでしょうか。図3で点Pを中心Oへ近づけていくと、点Qはどんどん遠ざかっていきます。それで、中心Oの反転は無限遠点とします(平面に「無限遠点」という1点を付け加える)。逆に、無限遠点の反転は中心Oとします。こうすることによって、全ての点が漏れなく1対1に対応します。
さて、反転の最も重要な性質は、直線と円が互いに変換するということです。正確に書くと、以下の4つの性質です。
(a) 中心Oを通る直線は、中心Oを通る直線に変換される
(b) 中心Oを通らない直線は、中心Oを通る円に変換される
(c) 中心Oを通る円は、中心Oを通らない直線に変換される
(d) 中心Oを通らない円は、中心Oを通らない円に変換される
(a)は図3を見れば明らかでしょう。
(b)は以下のようにします。
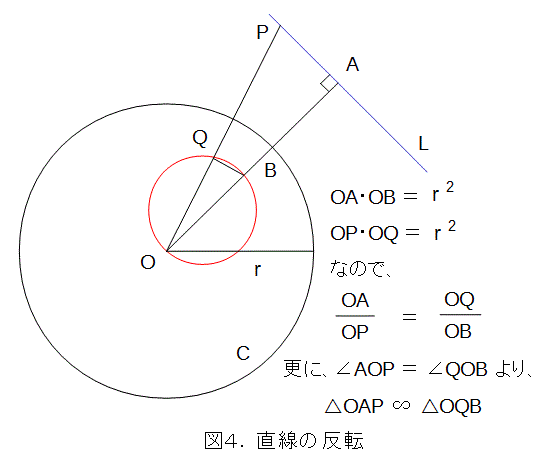
図4で、中心Oを通らない直線Lに対して、中心Oから下した垂線の足をAとし、Aの円Cにおける反転をBとします。また、点Pを直線Lの任意の点とし、その円Cにおける反転をQとします。
図4から、三角形OAPと三角形OQBは相似になります。すると、角OAPは直角なので、角OQBは直角です。したがって、点QはOBを直径とする赤い円の上にあります。これで、(b)が成り立っていることが解ります。
(c)は、反転の反転は元に戻ることから明らかでしょう。
(d)を示すにために、少し準備をします。
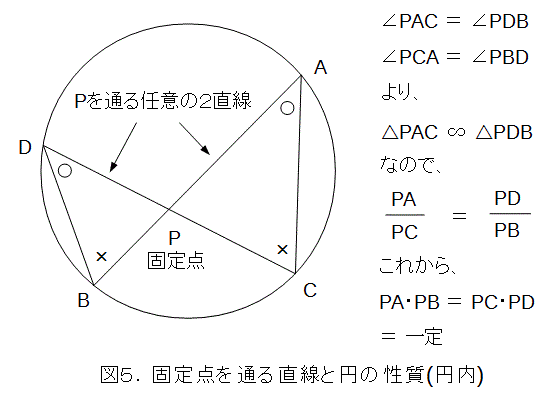
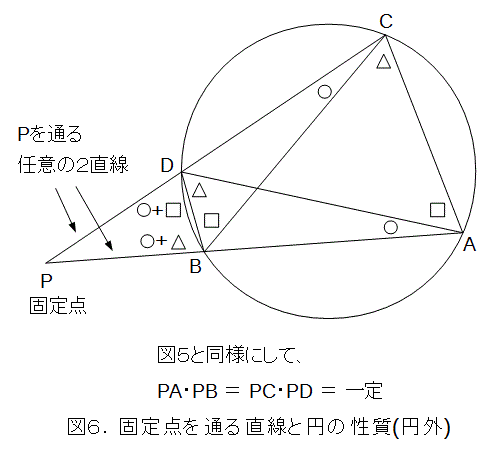
円と、点Pが与えられたときに、点Pを通る任意の直線が円と交わる点をA、Bとします。このときに、PA・PBは一定になります。Pが円周上にあるときは、積が0になるので自明です。それ以外のときは、任意に2本直線を引き、「円周角は等しい」という性質を使って、図5、図6のように示せます。
さて、円Cの中心をO、半径を r として、Oを通らない円Dの反転を考えましょう。円Dの中心をP、半径を s とし、Oから円Dへ任意に引いた直線との交点をA、B、その反転をそれぞれX、Yとします。また、OからPへ直線を引き、更に、Xを通ってPBと平行な直線を引いて、OPとの交点をQとします。
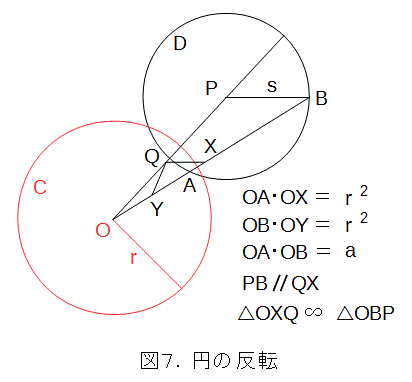
準備で述べたことにより、OA・OBは一定なので、簡単のために、その値を a とします。また、QXを t としておきます。


式(1)を式(2)で割って、
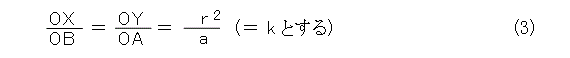
図7の三角形の相似についての記述により、

変形して、式(3)を用いると、
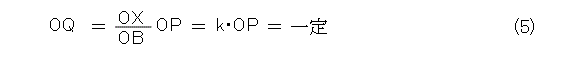
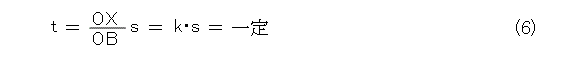
を得る。
ここで、式(5)、式(6)をよく見ると、Oから円Dへ任意に引いた直線に対して、著者のようにふらふらせず、常に、Qの位置は一定、また、QXの長さ t は一定になります。
これは、点Qが円の中心であり、t が半径であることを示しています。つまり(d)が成り立ちます。
4.コンパスで作図
反転の性質によって、円と直線が変換するということが解りました。これから、直線関係の作図も、ひょっとして円からできるのではないかという希望が出てきます。
それでは、反転の作図がコンパスだけでできるかどうかを考えてみます。
(期待) 中心O、半径 r の円Cによる、任意の点Pの反転Qはコンパスだけで作図できる。
最初に、点Pが円Cに乗っていると、反転QはP自身なので何もしなくても作図できたことになります。
点Pが円Cの外部にあるときを考えましょう。当然ですが、コンパスだけで作図するので、直線を引いてはいけません。直線は心眼で見ましょう。
Pを中心とし半径OPの円Dと、円Cとの交点をR、Sとし、それぞれR、Sを中心とする半径 r の円を描き、その円とOPとのOでない方の交点をQとします。
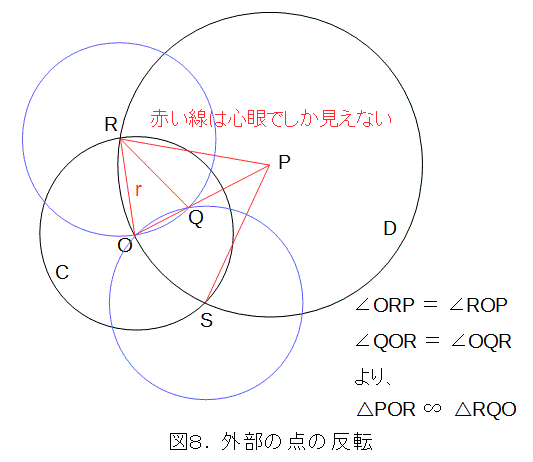
三角形の相似から、

これから、

となって、QはPの反転であることが解ります。
今度は点Pが円Cの内側にあるときを考えましょう。Pを中心として、半径OPの円と円Cが交われば、図8と全く同じなので問題ありません。やっかいなのは、半径OPの円を描いても、円Cと交わらないときです。
こういうときはどうするか。「やーめた。」とか「見なかったことにしよう。」というのはダメです。「交わらないなら、交わるようにしてしまえ。」と強引にいきましょう。基本的に、線分を拡大して、円との交点ができるようにします。
とりあえず、線分ABの2倍を作図します。言うまでもありませんが、直線を引いてはいけません。直線は心眼で見ましょう。
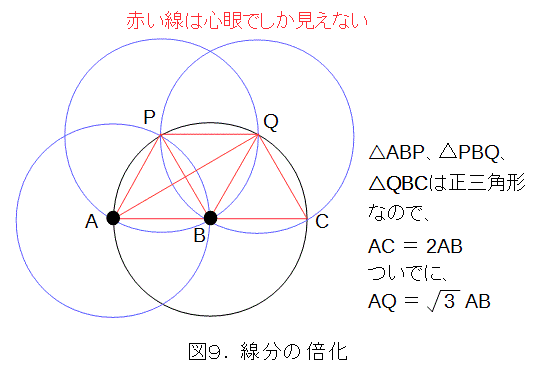
図9のように、Bを中心として半径ABの円を描き、点Aからはじめて、順次半径がABの円を描き、その円と元の円との交点を中心に円を描きます。そうすれば、線分ACは線分ABの2倍になります(円の直径)。ついでに、ABを単位長とすれば、コンパスだけで3の平方根の作図ができています。
同じ手順を繰り返せば、整数倍の作図が可能です。元に戻って、点Pが円Cの内側にある場合、OPを何倍かすれば円Cの半径 r よりも大きくなります。つまり、円Cの外部に出ます。なお、これを保障するのがアルキメデスの公理です。
いま、n 倍して円Cの外部に出たとします。そのときの点をQとします。

Qの反転をRとすると、
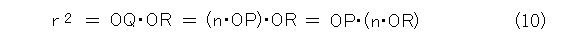
式(10)より、ORを n 倍した点がPの反転であることが解ります。
これで、反転を作図できることが示されました。ここで、OPを単位長とし、円Cの半径を適当にとって、OPの n 倍が円の外に出るようにして反転すれば、単位長の 1/n が作図できます。更に、これを m 倍すれば、m/n の作図が可能です。また、図9をBCからはじめてAを作図していると読み換えれば、負の数の作図もできています。これらにより、コンパスだけで有理数の作図は可能だと解ります。この辺の考え方は第94話でもやったような。
なんか、ひょっとして、コンパスだけで、定規とコンパスで作図可能なものを作図できそうな気分になってきましたね。少し、遊んでみましょう。
「線分の中点を作図(簡単)」(自分で作図しましょう)
線分ABに対して、

となるCを作図する。そして、Aを中心として、半径ABの円を描き、Cの反転をDとする。このときに、
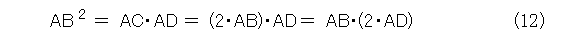
両辺をABで割って、

これで点DがABの中点であることが解り、中点はコンパスのみで作図できました。(有理数が作図できるのだから当たり前)
「円の中心を作図」(自分で作図しましょう)
これは、図8の逆読みでできます。
まず、中心が不明の円Dが与えられたとして、円D上に、任意に1点Oを取ります。次に、Oを中心として、適当な半径で円Cを描きます。この際に、図8のように、円Cと円Dは交わるようにします。その交点をR、Sとします。更に、点R、点Sを中心として、それぞれ半径がOR(OSに等しい)となるように円を描き、その交点の内、Oでない方をQとします。
円Dの求めたい中心をPとすると、図8から、Pの円Cに関する反転がQです。反転の反転は元に戻りますので、点Qの円Cに関する反転を作図すれば、それは点Pとなります。これで、円の中心を作図できました。
「円弧の2等分を作図」
中心Oの円が与えられたときに、円上の点A、Bに対して、弧ABを2等分する点Cの作図をしましょう。優弧、劣弧のどちらでも同じなので、弧ABは劣弧として作図します。
まず、A、Bを中心として、半径AOの円を描きます。次に、Oを中心として、半径ABの円を描き、A、Bを中心とする円との交点を、それぞれP、Qとします(実際には交点が2個できるが、以下全て、図にあるように選ぶ)。今度は、P、Qを中心として、それぞれ半径PB、QA(これらは等しい)となる円を描き、交点をRとします。最後に、PまたはQを中心として、半径ORの円を描き、弧ABとの交点をCとすれば、点Cによって弧ABは2等分されます。
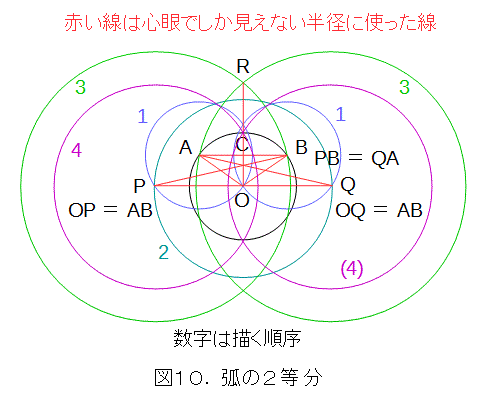
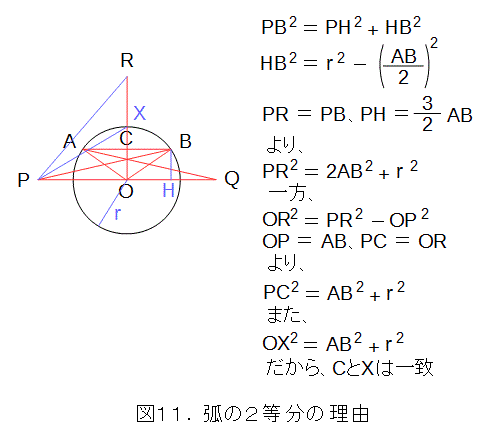
上記作図法によって、Cが弧ABの中点になっていることを示します。
中心Oで弧ABの乗っている円の半径を r とし、BからPQへ下ろした垂線の足をH、弧ABの中点をXとして、CとXの一致を示す方針で行います。概略説明は図11です。図を見て、詳細は自分で考えましょう。
では、いよいよ第2章で保留にした(2)、(4)について考えましょう。
直線と直線よりも、直線と円との方が考えやすそうなので、まずは(4)を考えます。円の中心をOとする円Cと、2点A、Bが与えられたとします。
A、Bの少なくとも一方が円C上にあれば、何もしなくても作図できたことになるので、A、Bは円C上にないとします。簡単のため、Aが円Cの外部、Bが円Cの内部にあるとしましょう。線分ABを有理数倍できるので、これで一般性を失いません。
例外となる方からやっていきましょう。直線ABが点Oを通っているとき、Aを中心として、半径OAの円を描き、円Cとの交点をP、Qとします。弧PQの中点が直線ABと円Cとの交点になります。弧PQの中点は作図できるので、交点は作図できました。
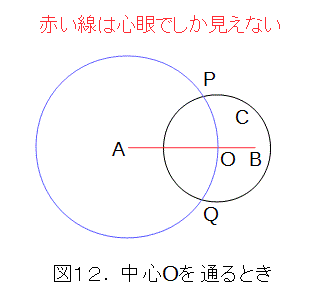
今度は、直線ABが点Oを通っていない場合です。
このときは、まず、A、Bを中心として、それぞれ半径AO、BOの円を描きそのOでない交点をPとします。次に、円Cに関してPを反転し、それをQとします(コンパスで作図可)。更に、Qを中心として、半径QOの円を描き、円Cとの交点をX、Yとします。このX、Yが直線ABと円Cの交点です。
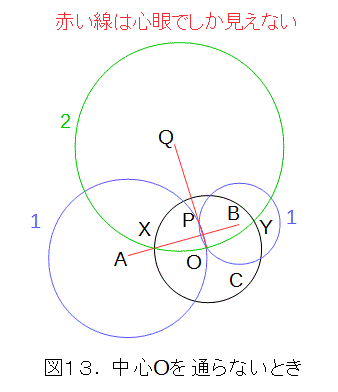
X、Yが、直線ABと円Cの交点であることを示しましょう。A、BはそれぞれO、Pから等距離にあります(青い円)。そこで、X、YもO、Pから等距離にあれば、二等辺三角形AOPの垂直2等分線上にあることになります。しかも、二等辺三角形AOPの垂直2等分線は直線ABなので、X、Yは直線ABに乗って完結します。
ところで、P、Qは互いに反転であり、図8のR、SをそれぞれX、Yに読み換えれば、O、Pから等距離にあることが解ります。
これで、直線と円の交点はコンパスだけで作図できることが示せました。
残る(2)を考えましょう。問題は、2直線の交点が作図できるかどうかです。しかし、これはやるまでもなく作図可能ですね。まず、2直線に対して、適当に円を描き、2直線の反転を作図します。この際に、直線の反転は円になるようにします。反転後は、円と円との交点の作図となります。円が与えられれば、円の中心は作図できるし、中心が解れば半径も解ります。また明らかに、円と円との交点は作図できます。後は、その交点を反転して作図完了です。
なお、円と円との交点は2点ですが、交点の1つは、反転に使った円の中心にきます(第3章の(b))。これを反転すると無限遠点にいくので問題ありません。自分で試してみましょう。
こうして、定規とコンパスで作図できるものは、全てコンパスだけで作図できるということが解りました。
5.正五角形の作図
おまけとして、円に内接する正五角形をコンパスだけで作図します。もともと、正五角形は定規とコンパスで作図できますので、今までやったことを使えば、コンパスだけで作図できます。しかし、このやり方は、ごちゃごちゃして面倒ですから、もっと簡単に作図する方法を述べます。
まず、与えられた円の中心をOとし、円上に1点Aを取ります。図9と同様に、Aを中心として、半径AOの円を描き、この円と元の円の交点をBとし、以下同様に、C、Dを取ると、正三角形が3個できます。
次に、A、Dを中心として、半径ACの円を描き、この2円の交点をPとします。
今度は、Aを中心として、半径OPの円を描くと、図10から、この円は弧BCの中点Qで交わります。
更に、Qを中心として、半径OAの円を描き、元の円との交点をS、Tとします。
最後に、S、Tを中心とし、半径OPの円を描き、その交点の内、Oに関してPとは反対側にある点をXとします。すると、AXの長さが、円に内接する正五角形の一辺の長さになります。
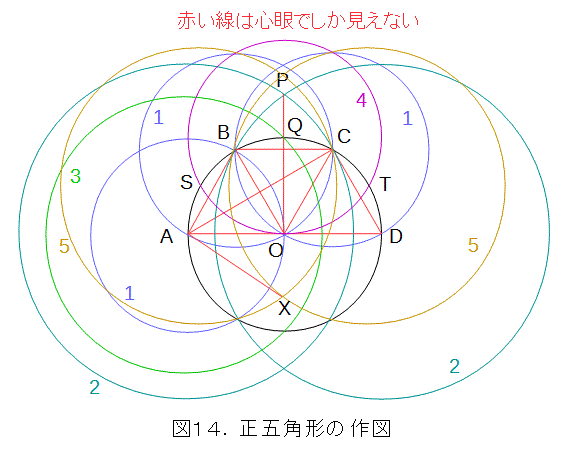
正五角形の一辺の長さが解ったので、後は、Aを中心として、半径AXの円を描き、元の円との交点を中心として、順次半径AXの円を描いていきます。これで円に内接する正五角形は、コンパスだけで作図できました。
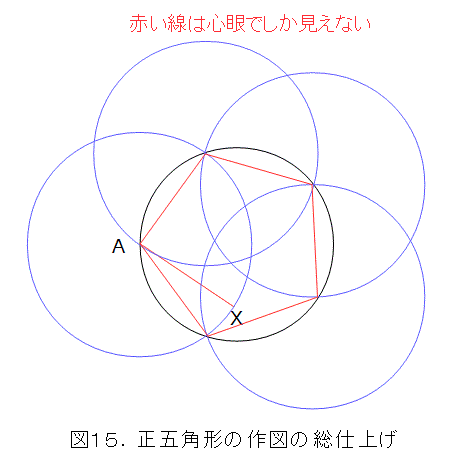
さて、残りを片付けましょう。AXが円に内接する正五角形の一辺になることを示します。
簡単のため、AOの長さを1とし、SからOPへ下ろした垂線の足をHとして、作図にしたがってAXを計算します。
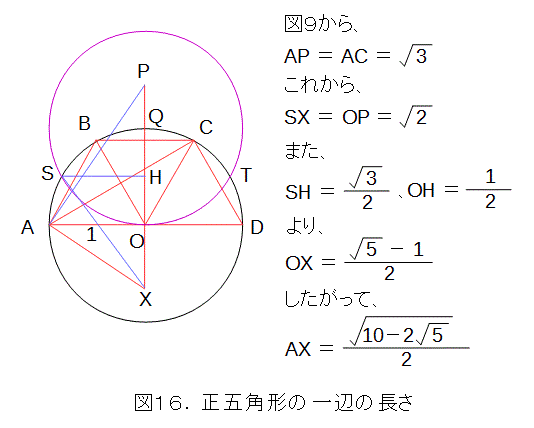
得られたAXは、単位円に内接する正五角形の一辺の長さなので、まさしく正五角形が作図できていたことになります。なお、理論的に、円に内接する正五角形の一辺の長さは求まります。これは、自分で計算して、AXの長さに一致することを確かめましょう。
6.おわりに
今回は、定規とコンパスで作図できるものが、全てコンパスだけで作図できるということを確かめました。しかし、これで終わりではありません。定規だけだったらどうなるでしょうか。実は、円が与えられたときに、定規だけでは円の中心を作図できません。この証明には、第95話で出てきた、射影幾何、特に射影変換の知識が必要になります。
定規だけでは作図できる範囲が狭くなるとしても、定規だけの作図問題はどうでしょうか。また、コンパスの使用回数に制限を加えて、何回まで使用を許したら、定規とコンパスで作図できるものを全て作図できるかが問題となります。
結論から言うと、コンパスの使用を1回だけに制限しても(定規は無制限に使用)、定規とコンパスで作図できるものは全て作図できます。今まで、コンパスを何回も使用していたので、この結果は驚きでしょう。
こう見てくると、作図は、「なんでぇ。作図なんて。」などとバカにできるものではありません。手を抜いていい加減にやると、誤った結論に至り(第91話、第92話)、真剣にやっても作図できなかったり(第80話、第86話)、制限しても作図できたりと罠だらけです。切り抜けるにはどうすればよいのでしょうか、本稿を読まれた方はどうお考えでしょうか。
完
平成28年2月20日
著作者 坂田 明治(あきはる)
|