|
第98話
ノギスの話
|

「主な対象読者」
今回はアナログ機器に使われている原理に興味を持つ人が対象です。具体的には、ものさしを2本使って、目で直接見るのが辛いような細かなものを扱えるようにすることです。
本 文 目 次
1.はじめに
2.ノギス
3.線分の等分割
4.くりこみ
5.おわりに
著者 坂田 明治
第98話 ノギスの話
1.はじめに
今回はノギスの話です。その昔、小学校か中学校のなんかの授業でノギスが出てきました。もっとも、家にノギスやマイクロメーターがあり、見慣れていたため、特に珍しいとも思いませんでした。
そういえば、ツベルクリン反応の腫れ(はれ)を調べるために、小型のノギスを使っていた記憶があります。当然ですが、我々バカガキは、ツベルクリン反応とか、BCGについて何も知らず、拷問としか思っていませんでした。「注射器」のことを「拷問器」と呼んでいたもんね(ハンコ注射となる前のことです)。そこで、ツベルクリン反応の測定前に、叩いたりぶつけたりして腫れを少しでも大きくし、なんとかしてBCG注射の拷問から逃れようとあがいていました。ちなみに、今では、ツベルクリン反応検査を省略してBCG接種されます(2005年度から)。
話をノギスへ戻しましょう。授業で、教師が、19ミリメートルを20等分しているから0.05ミリメートルまで測れるとかいっていたと思います。こんな天下り説明でいいのか 。
2.ノギス
最近はデジタルノギスが主流みたいですが、ここは昔ながらのアナログノギスを考えましょう。ホームセンター辺りでも、一応は売っていますので、実物を見たことがない人は、是非見に行きましょう。
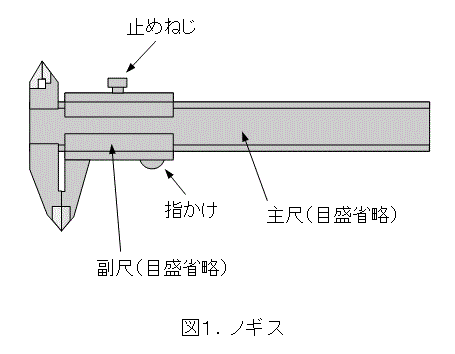
ノギスは色々な用途に使える精密機器です。なにせ、0.05ミリメートルまで測れるのですから。
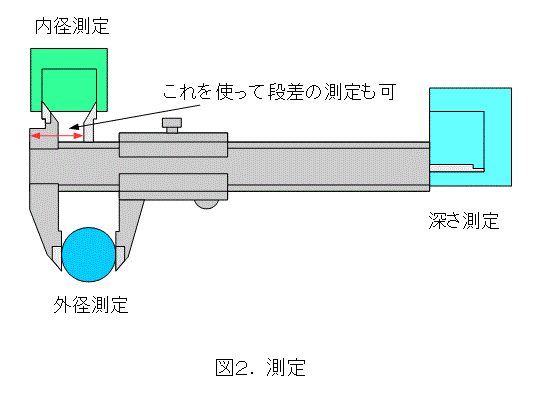
もちろん、測定には手練が必要です。0.05ミリメートルまで測れるということから、ちょっと傾けたり、余計な力をかけたりすると歪んでしまい、何を測っているのか解らなくなります。
更に、主尺と副尺の目盛を読み取るときに、読み取り誤差が発生します。その上、目盛を読み取っても、頭の中で長さを再構成しなければなりません。(再構成しなくてもすむように副尺の目盛をふっているものもあります。後で出てきます。)
これから話題にするのは、この主尺と副尺です。名前の通り、ものさしを2本使っています。
少し、ものさしについて考えましょう。まず、ものさしを2本使うと、足し算が測定できます。試しに、
3 + 14
をものさしで求めてみましょう。
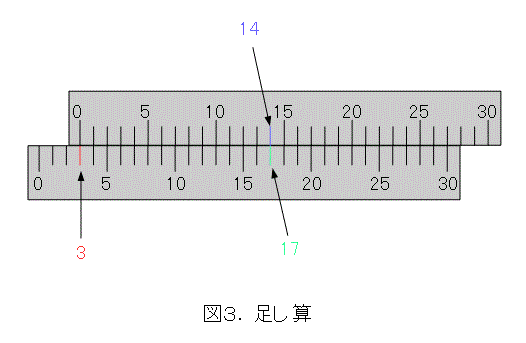
図3のようにして、計算しなくても 3 + 14 = 17 が求まります。引き算もできますので、自分で考えましょう。
普通のものさしは、足し算と引き算の測定ですが、「対数目盛」を使えば、掛け算と割り算が測定できます。この原理を利用したものが計算尺です。
昔は、計算尺が中学校で出てきました。やっぱり家にあったので、これも珍しくなかった。計算尺に関連して計算競技会やなんかの検定もあったと思います。
計算尺は問題がない訳ではなく、計算結果に誤差があり、更に、読み取り誤差もありました。それでも計算尺を使えば計算が楽になりました。
それが電卓の影響で、まったく計算尺を見ることがなくなるとは。こんなことでいいのだろうか。人間の叡智(えいち)が生んだ優れた発明や発見があまりにも簡単に失われすぎる気がします。どこかで対数の話をしようかとも思いますが、どうしたもんでしょうか。
3.線分の等分割
さて、ノギスでは0.05ミリメートルまで測れます。0.05ミリメートルは1ミリメートルの1/20ですから、1ミリメートルを20等分すれば、この測定ができるようになります。
線分の等分割は簡単な作図です。したがって、1ミリメートルの20等分割も簡単ですが、実際は無理です(線の太さが問題になるため)。それにできたとしても、目盛を読み取れないでしょう。
とりあえず、例として、線分を7等分割しましよう。
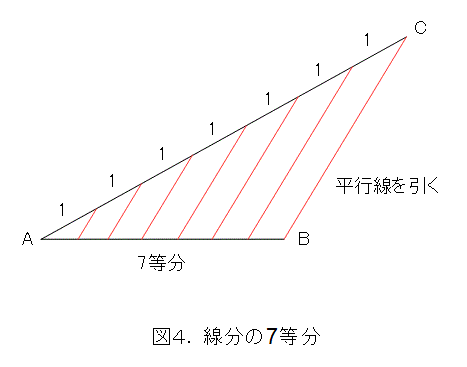
線分ABを7等分割しましょう。まず、点Aを通る適当な直線を引きます。その直線上に、コンパスで同じ長さ(ここでは1とします)になる点を順に7個取り、終点をCとします。
次に、点Cと点Bを直線で結び、先ほど取った全ての点からBCに平行な直線を引きます。この平行線と線分ABの交点が、7等分割点になります。
同じように20等分割も簡単にできます。しかし、実際に1ミリメートルを20等分するのは無理です。
4.くりこみ
まともな方法では1ミリメートルを20等分できず、したがって、0.05ミリメートルは作り出せません。では、どうしましょうか。真っ先に浮かび上がるのは、「あきらめる」ことですけど。
問題なのは、1ミリメートルが小さすぎて、20等分できない(これができる筆記具を持ってない)ということです。小さすぎてダメなら、拡大することを考えましょう。
主尺と副尺を用意します。主尺は基本的な長さを測るものなので、目盛をいじれません。手を加えるとすると、必然的に副尺の方になります。そこで、副尺の目盛(1ミリメートル)に、0.05ミリメートルをくりこみます。
このようにすると、主尺と副尺の目盛の差は0.05ミリメートルとなり、前章で書いた1ミリメートルを20等分するよりはやりやすそうな気がします。
何をやっているのかというと、1ミリメートルを20等分して0.05ミリメートルを作るという直接的なやり方をやめて、主尺と副尺の目盛の差として間接的に0.05ミリメートルを作ろうということです。
さて、くりこむのに、足し算でくりこみましょうか。それとも引き算にしましょうか。今のところ、どっちがよいか解らないので、両方考えてみましょうね。
まずは、引き算でくりこみます。1目盛である1ミリメートルから0.05ミリメートルを引くので、
1 - 0.05 = 0.95
となり、1目盛が0.95ミリメートルになります。
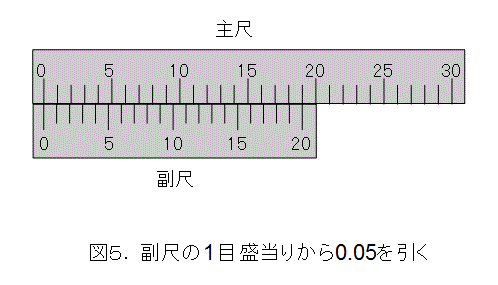
0.95ミリメートルを20倍すると丁度19になるので、副尺の20目盛は、主尺の19ミリメートルのところと一致します(もちろん主尺と副尺の0を合わせる)。これで、副尺の目盛は、19ミリメートルを20等分すれば作れることが解りました。しかも、1ミリメートルを20等分(無理だってば)するより、19ミリメートルを20等分する方が現実的にできそうです。
なお、注意点があります。0.05ミリメートルを引き算で組み込んだ結果、19ミリメートルを20等分にすればよいと出てきました。これは、19ミリメートルを20等分ということから始めたものではありませんね。本稿のやり方では、はじめにで出てきた教師の出発点が結論になります。この点はしっかり抑えておきましょう。色々な応用を考える上で道標(みちしるべ)となりますので。
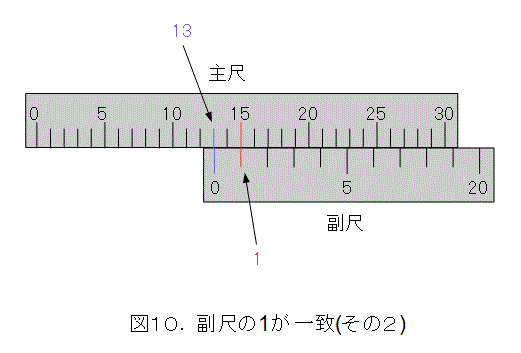
では、一致した目盛から何がいえるのかを考えましょう。図6のような場合です。以下、ノギスで考えていることをお忘れなく。ついでに、図2の青丸を測っているとイメージしましょう。
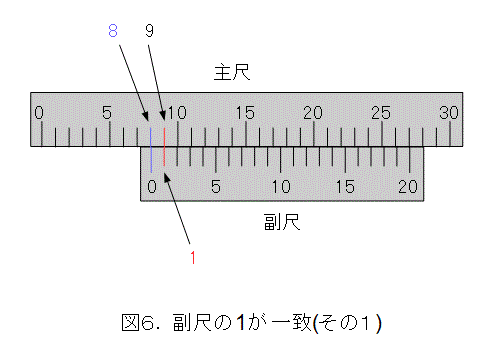
このときは、まず、主尺と、副尺の0を見て、測った物体が8ミリメートルちょいの長さであることが解ります。なお、長さを測っている主体は主尺です。副尺は、これを補助しているとの位置づけになります。
更に、副尺の1の目盛線が主尺と一致しています。したがって、副尺の0の位置は、主尺の9から副尺の1目盛分少ない位置になります。つまり、
9 - 0.95 = 8.05
となり、青丸の外径は8.05ミリメートルと求まります。図5のちょっと上の式を代入すれば、
9 - ( 1 - 0.05 ) = 9 - 1 + 0.05
= 8 + 0.05
として計算できます。(普通はこっちを使う)
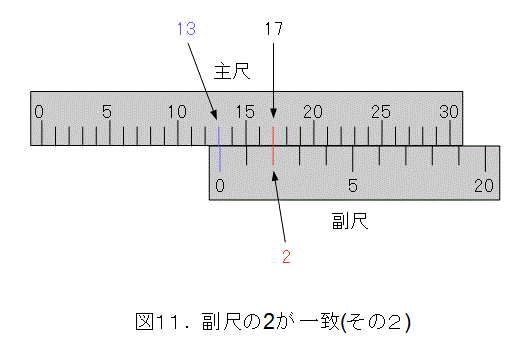
今度は、図7の場合を考えます。
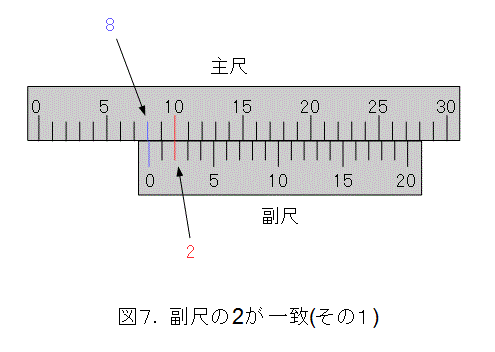
このときも、まず、主尺と、副尺の0を見て、やっぱり測った物体が8ミリメートルちょいの長さであることが解ります。
更に、副尺の2の目盛線が主尺と一致しています。したがって、副尺の0の位置は、主尺の10から副尺の2目盛分少ない位置になります。つまり、
10 - 0.95 ・ 2 = 8.10 (「・」は掛けるの意味。掛け算記号は文字化けしそうなので)
となり、青丸の外径は8.10ミリメートルと求まります。もちろん、図6の説明と同じ理由で、
8 + 0.05・2 = 8 + 0.10
としても計算できます。(普通はこっちを使う)
以下同様にして、とにかく、副尺の目盛り線が一致すれば、青丸の外径が求まります。
金属の加工精度は無視して、もっとノギスの精度を上げてみましょう。今までは、0.05ミリメートル単位で考えていましたので、これを倍の精度にしましょう。1ミリメートの20等分の倍で40等分です。計算すると、0.025ミリメートル単位ですね。これを副尺へくりこみます。
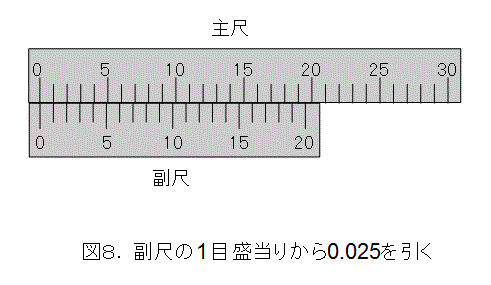
これで、倍の精度で測定ができます。そして、副尺の40目盛は主尺の39ミリメートルのところで一致します(もちろん主尺と副尺の0を合わせる)。つまり、副尺の目盛は、39ミリメートルを40等分すれば作れるということが解りました。
同様にして、望む精度で測定用の目盛を作ることができます。手順は、まず測定精度を決め最小単位を作ります。これを副尺へくりこみ、その上で、主尺と目盛が一致するところを求めます。たとえば、1ミリメートルの1/30を測定したかったら、これを副尺へくりこんで、29ミリメートルを30等分すればできます。上の方で述べた注意点は、このような形で効いてきているが解るでしょう。
さて、図8へ戻って、副尺の目盛を2目盛間隔に間引きましょう。これは、精度0.025ミリメートルを半分の精度0.05ミリメートにしたものと同じです。したがって、目盛の幅を広げて精度はそのままです。
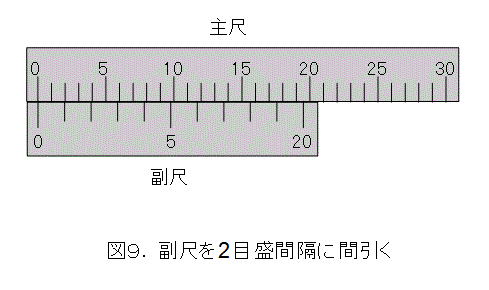
図6、図7と同様にして、0.05ミリメートが測れていることが解ります。
こちらの方が目盛が広くて見やすくなります。その上、目盛が広いということは、数字が書き込みやすいことでもあり、図12のように数字をつければ、余計な計算をしないでも測れるということにもなります。

精度が思いのままというところから、このようなことまで出てきました。
次に、足し算でのくりこみを考えましょう。
1目盛である1ミリメートルに0.05ミリメートルを足すので、
1 + 0.05 = 1.05
となり、1目盛が1.05ミリメートルになります。

1.05ミリメートルを20倍すると丁度21になるので、副尺の20目盛は、主尺の21ミリメートルのところと一致します(もちろん主尺と副尺の0を合わせる)。これで、副尺の目盛は、21ミリメートルを20等分すれば作れることが解りました。
では、目盛線が一致したところから何がいえるのかを考えましょう。図14のような場合です。
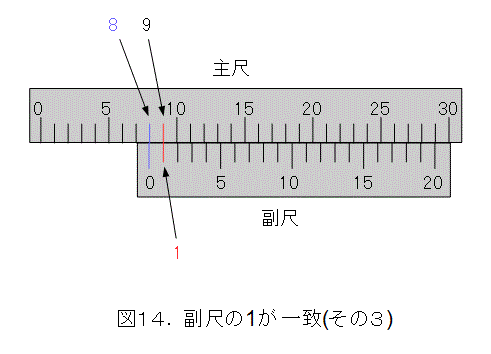
このときは、まず、主尺と、副尺の0を見て、測った物体が8ミリメートルより、ちょい短い長さであることが解ります。
更に、副尺の1の目盛線が主尺と一致しています。したがって、副尺の0の位置は、主尺の9から副尺の1目盛分少ない位置になります。つまり、
9 - 1.05 = 7.95
となり、7.95ミリメートルと求まります。図13のちょっと上の式を代入すれば、
9 - ( 1 + 0.05 ) = 9 - 1 - 0.05
= 8 - 0.05
として計算できます。
今度は、図15の場合を考えます。
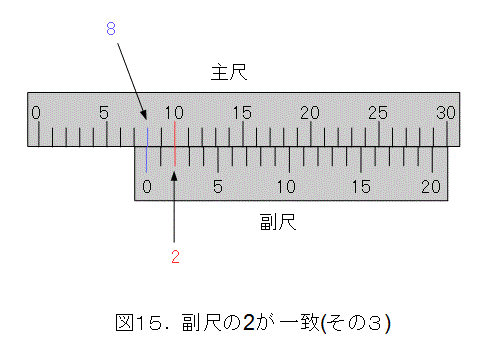
このときも、まず、主尺と、副尺の0を見て、やっぱり測った物体が8ミリメートルちょい短い長さであることが解ります。
更に、副尺の2の目盛線が主尺と一致しています。したがって、副尺の0の位置は、主尺の10から副尺の2目盛分少ない位置になります。つまり、
10 - 1.05 ・ 2 = 7.90
となり、7.90ミリメートルと求まります。もちろん、図14の説明と同じ理由で、
8 - 0.05・2 = 8 - 0.10
としても計算できます。
以下同様にして、とにかく、副尺の目盛り線が一致すれば、長さが求まります。
結局のところ、引き算でくりこんでも、足し算でくりこんでも大差ないということが解りました。もっとも、目盛を読んでから、足し算で計算する方が、引き算で計算するよりも楽っぽいけど(あくまでも「っぽい」)。
5.おわりに
今回は、アナログノギスを念頭に、2本のものさしについて考えました。目盛の工夫と、2本のものさしの使い方によって、よく見えないような細かな単位を読み取れるようになりました。すごいことだと思います。
アナログノギスはまだ残っているので、手にとって確かめることもできますが、計算尺の方は、とっくに製造を止めており、よほどのことがないと手に入りません。それは、対数目盛のついた2本のものさしについての知恵を見る機会がないことを意味します。こんなことでいいのでしょうか。
デジタルがいいとか悪いとかではありませんが、一般的に、デジタルは中身がブラックボックス化しており、アナログは原理が見えています。そして原理が見えていれば、そこに興味を持つ可能性も出てきます。将来のことを考えると、たとえ実用性は劣るとしても、少しでもいいから、アナログ機器を残しておくことに意味があると思います。この点について、本稿を読まれた方はどうお考えでしょうか。
完
平成28年5月28日
著作者 坂田 明治(あきはる)
|