|
第99話
ブール代数の話
|

「主な対象読者」
本稿の目的は、先を目指すための実験です。具体的には、予想を立てて、それを確認するという方向の実験です。全てにおいて、予想を立てることは重要です。これは、予想が当たっているかどうかではなく、予想を立てること自体が思考訓練として重要という意味です。今回は、予想を立てて、それを調べるという方向へ誘導する都合上、当たりばかりです。しかし、外れを出し、その上で考え直すことの方が、より重要であるため、今後の取り組みに残します。
本 文 目 次
1.はじめに
2.ベン図
3.ブール代数
4.同型
5.有限ブール代数
6.ストーンの定理
7.おわりに
著者 坂田 明治
第99話 ブール代数の話
1.はじめに
理科好き子供の広場は簡単すぎて面白くないようです。「激ムズでいーから。」という人がいました。まあ、他の意見は何も出てこないため、これが全てかどうかは解りません。
しかし、「激ムズでいーから。」という人がいる以上、この人の要求にも応えようと思います(つまり、本稿はこいつのためだけに書いたということ)。今回は、ほんのちょっと難しい世界に入ろうではありませんか。
なお、当初予定していたのは、「0と1の世界(仮称)」でした。0と1だけの世界で関数を考え、それがどうなるかを調べるという話です。0と1だけなので、2で割った余りの世界と考えてもよいし、命題論理や真偽表の世界と考えてもよいし、また、一番簡単なブール代数とも考えられます。この上で、シェファー関数を扱うつもりでした。
今回、ちょっとだけ難しい世界に入ろうということで、予定を変更してブール代数の話にします。よく使う概念ばかりなので、考え方の基本を身に付け、自由に使えるようになりましょう。
2.ベン図
ベン図をまともに扱うと、理科好き子供の広場1回分の量になってしまうため、ちょっと触れるだけにします。(証明等は読者の宿題とすればいいや)
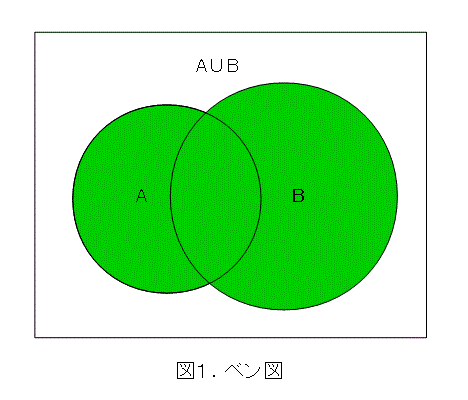
図1のようなのがベン図ですね。共通集合、合併集合、補集合、包含関係について、理解をたすける上できわめて有用な手段なので、ベン図を描きましょう(と、昔、学校の先生が言ってました)。
ところで、一般的な4つの集合のベン図を図2のように書く人がいます。
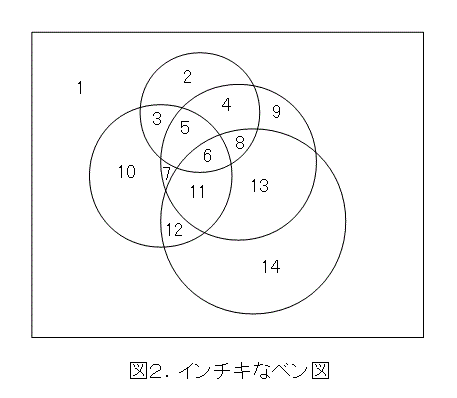
4つの集合があれば、できる領域(集合)は2の4乗(16)になるので(領域の数の求め方は読者の宿題)、この図はインチキです。そもそも、円4つでは16個の領域(集合)を作れません。もちろんこの証明は読者の宿題です。
では、どうやってもダメかというと、そうでもありません。実際に16個の領域(集合)を作る方法はあります。
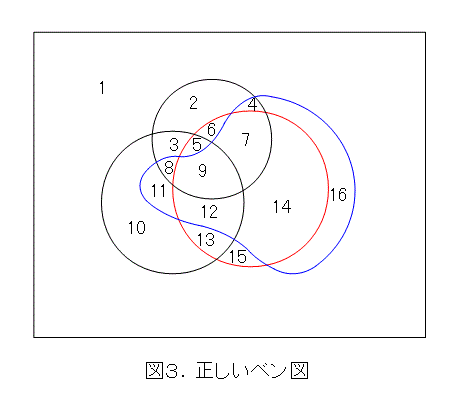
作り方は以下です。
まず、3個の円を普通に描きます。それから何でもいいから、1つの円に注目します。図3の赤い円に注目しましょう。赤い円の近くに、適当に点を取って、赤い円に沿って曲線を描きます。図3では赤い円の右辺りに点を取って、反時計回りに曲線を描いています。その上で、他の曲線を横切ると、すぐに赤い円を横切るように曲線を描きます。そして、赤い円を横切ったら、また、赤い円に沿って曲線を描きます。以下、これを繰り返し、出発点と連結して閉曲線にします。
こうすると、16個の領域(集合)ができます。図3がそうなっているでしょう。5個の集合についても同様です。4個の集合、つまり図3を元に、どれか1つの曲線に注目して、上に書いた手順で描けばできます。これを描くのも読者の宿題です。
6個以上も全く同様にして描けます。当然ですが、こうすれば何個の場合でも描けるという証明が必要ですね。当然のように読者の宿題です。
さて、ここで問題があります。えっ、手抜きで読者の宿題にばかりするのが問題だって。まあ、そういう意見は無視して、問題というのは、空集合をベン図に描けません。空集合は、全ての集合の部分集合なので、全ての集合に入っている必要があり、描きようがありませんね。
してみると、ベン図は空集合にあまり有効ではない。ただし、2つの円を離して描いて、互いに素であることは描けますので、全くの無力という訳でもありません。
ここまでの考察で、図3みたいに4個の集合相手では、結構複雑になること、また、空集合に対してはあまり有効ではないことを考慮に入れ、ベン図は1個から3個までの集合に対して有効な手段と考えるべきでしょう。もちろん、4個以上でも、一般的な集合を描くのでなければ有効な場合もあります。
このように、無闇に「有効な手段」と言うのは危険です。上で書いたように、特定の場合だけにしか通用しないことがあるからです。したがって、有効な手段と言うときは、どんなときが有効で、どんなときがまずいか説明できるようにしましょう。これは、普段の生活でも、都合のいいことばかり言ってリスクを説明しないものは危険と考え、そんなことを言ってる奴らを信用しなくなるのと同じです。
3.ブール代数
さて、都合のよいことに、集合にはいくつかの演算が用意され、おまけに包含関係という関係まで用意されています。その上、空集合と全体集合というありがたい集合まであります。ここでは、空集合を 0 、全体集合を 1 と書くことにします。以下、全体集合は空集合ではないとします(全体集合まで空集合だと、どうでもよくなって面白くありません)。このとき、 0 と 1 だけでも色々できますが省略します。
まず、集合に関する演算から見ていくことにしましょう。色々あるが、ここで使うのは、合併集合、共通集合、補集合です。書き方も色々あるのだけど、次のように書くことにしましょう。

ところで、等号について、当たり前と思い、何も考えていない人も多いでしょう。折角なので、等号についても考えます。ここでは、以下の4つの性質を満たす関係が等号です。(それにしても、ろくな記号が用意されてない上に文字化けしやがる。余計な手間がかかってたまらん。)
任意の集合 a 、 b 、 c に対して、

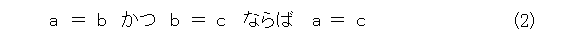
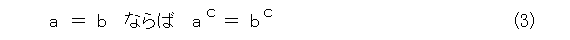

が成り立つとき、「=」を等号と呼ぶ。
はじめに、集合について、次の性質が成り立ちます。自分で、ベン図を描いて確認するなり、証明するなりしましょう。なお、結合法則が成り立つので、適当に( )は省略できるようになります。それから、一々書きませんが、ある集合の部分集合の全体で演算を考えています(要するに、全体集合は固定して、その部分集合しか考えていないということ)。
任意の集合 a 、 b 、 c に対して(以下、このように書いたときは、なんかの集合の任意の部分集合という意味)、
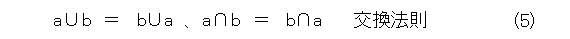
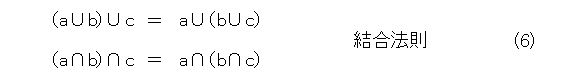
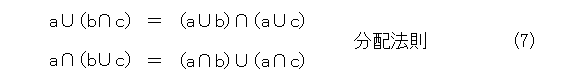

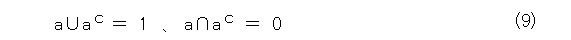
が成り立つ。
これらの性質を使うと色々でてきます。例えば、 0 はただ1つだという当たり前のことが出てきます。
もう1個あったとして、 a とすると式(8)を満たす、そして、

となるから、ほら、等号の意味で一致して1個でしょう。
同様にして、 1 がただ1個だということも出てきます。
更に、べき等法則というのも出てきます。
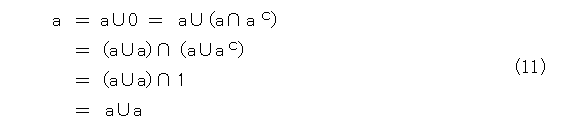
その他色々でてくるが省略(ド・モルガンの法則とか)。
ここで、式(5)〜(9)をよく見ると、合併集合と共通集合を入れ替えて、更に、 0 と 1 を入れ替えても式が全く変わりません。これは「双対的」という性質で、手抜きに使えるが、これも省略。
次に、包含関係に目を向けましょう。包含関係は以下の性質を満たします。
任意の集合 a 、 b 、 c に対して、



が成り立つ。
式(12)〜(14)が成り立つとき、この関係を順序関係と呼びます。したがって、包含関係は順序関係です。ところで、

なので(証明は読者の宿題)、式(12)〜(14)は式(5)〜(9)から導けます。当然これも読者の宿題です。(上の式を双対化したものも考えておくこと)
更に、任意の集合 a に対して、

も成り立ちますが、やっぱり読者の宿題です。
ここまでくると、
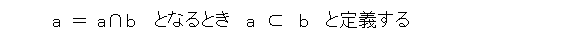
とやれば、式(5)〜(9)によって順序となることが解ります。つまり、式(5)〜(9)が基本で、これさえあればよいということです。ついでに、次の式(15)も成り立つので、証明は読者の宿題です。
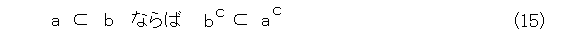
そこで、式(5)〜(9)を公理系として、ブール代数を定義付けられそうですね。
具体的には、まず、全体集合をXとします。このとき、Xは少なくとも2個以上の要素を持つとします( 0 と 1 があって、しかも異なっていないと面白くないから)。そして、演算が3種類定義できているとします(ろくな記号がないので、演算記号は合併集合、共通集合、補集合のものをそのまま使う)。

なお、演算が定義できているということは、その演算について閉じていることです。その上で、式(5)〜(9)が成り立つとき、

をブール代数と定義します。以下、特に指定がない限り、ブール代数と言えばこれのことです。
今までやってきた集合の例は、集合Xがある集合の部分集合を要素とする集合です。このように、集合を要素とする集合のことを集合族とも言います。そして、ある集合の部分集合を全て要素とする集合のことをべき集合と呼びます。
4.同型
同型について考えましょう。つまり、なんかとなんかが同じ(とみなせる)かどうかという問題です。最初に、ただの集合だけで考えましょう。これは一致するかどうかだけです(等号が成り立つかどうかだけ)。後で出てくる1対1の写像で結ばれているものを同じ(濃度が等しいという)とすることもできますが、これ以上何かが出てきそうな気がしませんね。
そこで、集合に何らかの構造を導入して考えます。つまり、集合をA、Bとして、(A : 構造1)と(B : 構造2)を考えて、同じかどうかを調べるということです。構造まで考えると、とたんに話がぐちゃぐちゃして・・・、もとい色々出てきて話が面白くなります。
例えば、Rを実数全体の集合として、(R : 足し算)と(R : 掛け算)を考えます。このとき、集合としては同じでも、構造が異なるため別物になります。足し算では全ての数に対して逆元がありますが、掛け算では 0 の逆元(逆数)がないからです。こうして、(R : 足し算)と(R : 掛け算)は別物となります。
次に、R+ を正の実数として、(R+ : 掛け算)と(R : 足し算)を考えましょう。底はなんでもいいので書かないことにして(一応、底を10とする常用対数としておく)、対数の性質から、

が成り立ちます。
式(16)をよく見ると、正の実数の掛け算が、実数の足し算に対応していますよね。交換、結合、単位元、逆元もぴったり対応しています。つまり、集合としては別物でも、
(R+ : 掛け算)と(R : 足し算)は構造まで含めて考えると同じものになります。
では、こんなことして何が嬉しいのでしょうか。掛け算を計算するのは大変面倒です。ごちゃごちゃした数字の掛け算はやりたくないですよねぇ(こんなことでいいのか)。一方で、足し算は、計算しなくても2本のものさしで測定できます(第98話に書いてある)。
すると、対数関数による対応によって、2本のものさしで掛け算を測定できることになります。

この事実をうまく使ったものが計算尺です。図4のように、対数関数と指数関数の行きと帰りの部分をなんとかすれば、ものさし2本で測定できることが解ります。つまり、同じものとみなすことによって、都合のよいものを持ってきて、都合よく事を運ばせられるということです。
対数関数に関して、もう少し見ておくと、対数関数は、正の実数から、実数への1対1対応です。そうすると、式(16)と合わせて、集合の部分で1対1対応になり、構造の部分もきっちり対応させています。
以上の考察から、同型(同じとみなせること)を考えましょう。集合をA、Bとして、
(A : 構造1)と(B : 構造2)が同型であるというのは、AとBが1対1に対応し(全単射)、その対応をする写像によって、 構造1が 構造2に対応付けられるというのが妥当でしょう。また、先の例では構造として演算を考えましたが、必ずしも演算だけが構造ではありません。もっと別のものもありです。
AとBの1対1を外して、準同型を考えることもできますが、今回は使わないので省略します。
ここまでの準備をしておいて、ブール代数の同型を定義しましょう。基本は、集合の間で1対1の写像があり、その写像が構造をうまく移していることです。
2つのブール代数、
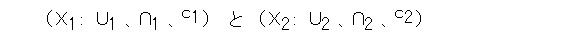
が与えられたときに、X1 からX2 への1対1の写像(全単射) f が、以下を満たすとする。
x 、 y をX1 の任意の要素として、
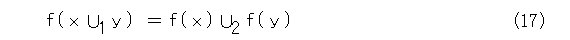
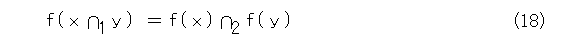

が成り立つとする。
このときに、 f を同型写像、
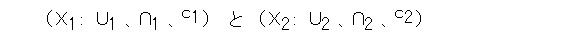
を同型という。
f の逆写像 f-1 も同型写像になりますが、これも簡単なので読者の宿題です。また、
ド・モルガンの法則を使えば、式(17)と式(18)はどちらか一方のみで十分です。これも読者の宿題。
同型という概念が導入できたので、ブール代数がお釈迦様の掌(てのひら)から外に出られたかどうかが考えられるようになりました。つまり、「ブール代数なんて仰々しく定義したけども、これは適当な集合族に、合併集合、共通集合、補集合を演算として入れたものと同型になるんじゃないのか。」(要するに名前を変えただけ)という問題を考えるということです。
5.有限ブール代数
既に見たように、ブール代数には順序を導入できましたね。まずは、順序について考えましょう。ブール代数であることをしばらく忘れて、順序だけ考えます。式(12)〜(14)が成り立っているのが順序でした。なお、ここでも、包含関係を表す記号を順序記号として使います。どうしてもイヤだという人は、式を等号付き不等号に書き直しましょう。
最初に、Xをなにかの集合として、ここに順序が入っているとします(このときにXを順序集合と言う)。そして、特に指定のない限り、出てくる文字はXの要素であるとします。以下、辛く苦しい用語だけの定義が続きます(書いている方が、面倒で辛いという意味)。
任意の a 、 b に対して、

の少なくとも一方が成り立つとき、線形順序と呼びます。このとき、Xは線形に順序付けられているといいます。自然数や実数などで、等号付き不等号は線形順序ですね(要するに1本に並べられるということ)。
任意を取ってしまって、なんか解らんけど a 、 b に対して、

が成り立つとき、 a 、 b は比較可能であるといいます。普通に考えて、集合では比較可能にならないものがあります。第1図のような場合は、どちらも互いに含まないので、比較可能にはなりませんね。
人間は、なにかにつけ順序を付けるのが好きです(しかも好き嫌い順序が1番好きで、人事評価もこれでやったりする)。なにがしかの基準(言い訳)を付けて、無理やり順序を付けます。例えば、学校の同一学年の生徒を、試験の成績で順序付けたりします。ちなみに、(本稿の都合で)試験の点数が同じときは、何らかの補足事項(えこひいき)を使って一意に順序付けしましょう。以下、全国模試でも同じ。(こういうのを大人の事情といいます)
でも、こっちの学校で付けた順序は、あっちの学校(一応、ライバル校という設定)では通用しません。試験の問題が違い、こっちの学校の生徒と、あっちの学校の生徒は比較不可能です。もちろん、あっちの学校は、あっちの学校でやった試験で順序付けされています。
これから、順序集合Xの部分集合で、線形に順序付けされているものを考えることに意味がありそうです(あっちこっちの学校ごと、線形に順序付けされているから)。そこで、順序集合Xの部分集合で、線形に順序付けされている集合を線形順序部分集合と呼びます(そのまんまの名前じゃないか)。
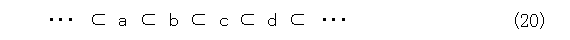
線形に順序付けされているものは、式(20)のように書けることから、鎖ということもあります。
ここから先、もうちょっとだけ順序関係の言葉を用意します。

のとき、 a は b より小さいとか、 b は a より大きいということにします。
こっちの学校とあっちの学校とは比較できませんが、こっちの学校で成績トップとか、あっちの学校で成績トップとかいうやつがいますよね。そこで、こういう成績トップのやつらを指定できるように、極小という言葉を用意しましょう。
順序集合Xとその要素 a において、Xが要素 a より小さい要素を含まないとき、 a を極小であるという。
つまり、Xを全ての学校の同一学年の生徒の集合とすれば、こっちの学校の同一学年のトップは極小です。もちろん、あっちの学校の同一学年のトップも極小です。
同様にして、極大も考えられます(こちらは成績が・・・)。続いて、順序集合Xの全ての要素より小さい要素があれば、それを最小と呼びます(ここでの「より小さい」は自分自身も含むということに注意しよう。自然数や実数などでは、等号付き不等号のことでした。)。全国模擬試験をやれば、全国同一学年成績トップが出ます。こいつが最小です。
最小な要素は、もしあれば、1つです。それは以下で解ります。
最大も同様です。
全国模試をやると、今までこっち校とあっち校の成績争いだったものに、そっち校が絡んできたりします。しかも、そっち校は試験対策が進んでいて点数もよく、そっち校の成績下位者が、こっち校のどんな人よりも試験の点数がよかったりします。
こうなると、そっち校の成績下位者の中に、こっち校の成績トップより上の生徒がいることになります。こっち校は面目丸潰れですね。
このことを元に用語を導入しましょう。
順序集合Xの部分集合Yで、Yのいかなる要素 y に対しても、

となるXの要素 x が存在するとき、 x をYの下界と呼び、特に、下界の集合が最大値を持つとき、その最大値を下限といいます。
上界と上限も同様です。そして、順序集合Xの空でない全ての部分集合に対して、常に上限と下限があるとき、順序集合Xは完備であるといいます。
あと一つ、極小の概念っぽい用語を用意します。順序集合の要素で、その要素より小さい要素が、その要素自身か、最小要素しかないときに、この要素を原子と呼びます。
さて、ここから有限集合について考えましょう。有限と付いただけで、色々な性質が成り立ってきます。
例えば、要素が有限個の線形順序部分集合は最小要素と最大要素を持っています。
この証明は簡単です。何でもいいから、要素を1個取り出します。すると、この要素は、最小か最小でないかのいずれかです。最小ならそれまで。最小でなければ、それより小さい要素が存在するので、それを取り出します。この要素が最小であればそれまで。最小でなければ、更に、それより小さい要素が取り出せます。以下、これを繰り返します。元々、要素は有限個しかないから、有限回でこの処理は打ち切られ、最小の要素は見つかります。最大要素も同様です。
ブール代数に戻って考えましょう。引き続き、要素が有限の場合です。まず、ブール代数は順序を持っていました。
集合のブール代数の場合、全体集合が集合族でした。ちょっとややっこしくなるので、少しブール代数の例を眺めてみましょう。
最初は、要素が1個だけの集合からブール代数を作ります。1個しかない要素を a とします。このとき、考えている集合は、 { a } なので、全体集合は以下のようになります。

次に、要素が2個の場合を考えます。2個の要素を a 、 b とすると全体集合は以下のようになります。
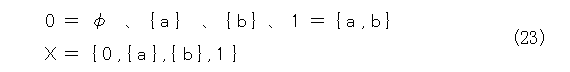
順序が小さいほうを下にして図を描くと以下のようになります。
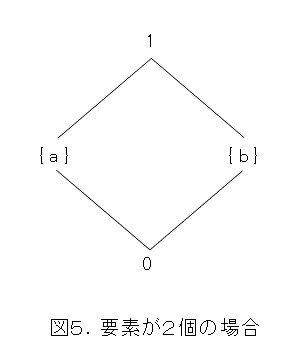
要素が3個の場合を考えましょう。3個の要素を a 、 b 、 c とすると全体集合は以下のようになります。
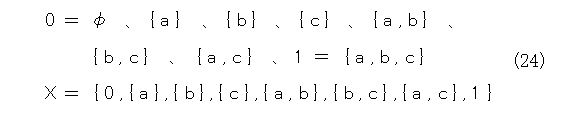
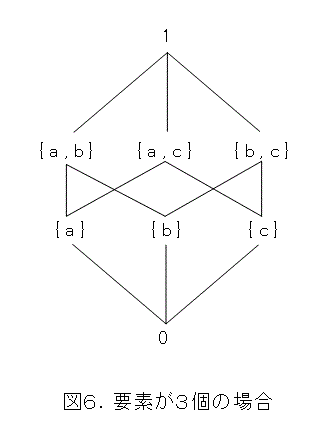
要素が4個以上の場合は自分で書いてみましょうね。
図を眺めてみると、原子の存在が予想されます。これを確かめるのは簡単です。なんでもいいから、要素を1個とります、するとそれが原子だったらそれまで、原子でなかったら、それより小さくて、 0 ではないものが存在します。それが原子だったらそれまで、原子でなかったら、と繰り返します。有限個しかないので有限回で終了して原子の存在が示せます。以前、同じようなことをやりましたね。
ここで、有限ブール代数(全体集合の要素数が有限個)を、

とします。
とりあえず、原子に着目します。図6を眺めて、どの要素でも、注目している原子より大きいものと、「そんな原子関係ないや」というものに分かれます。手で確かめてみれば、「そんな原子関係ないや」というのは c を取ると最初の「そんな原子」より大きくなります。これらを式で書くと、原子を x 、 y を任意の要素として、
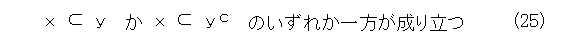
ということです。それを調べましょう。
もし、

が成り立つとすると、式(15)を式(26)の第1式に適用して、

となるので、

したがって、

これは、 x が原子であることに反するから、式(26)はありえない。
次に、

で、 x は原子だから、
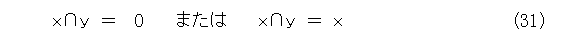
が成り立つ。これから、
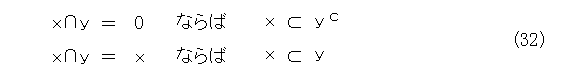
が成り立つ。式(32)の第1の式が成り立つことは読者の宿題。
これから、式(25)が成り立つ。
式(25)から、原子によってXは2つのクラスに分割されることが解りました。このことから、原子が決定的に重要な役割をしてると予想されます。
そこで、原子の拾い出しをやりましょう。 y より小さい原子全体の集合を f ( y ) とします。
まず、Xの任意の要素 y 、 z に対して、
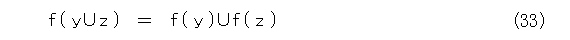
を導きましょう。ただし、式(33)の左辺の合併集合記号は、ブール代数での記号で、右辺の合併集合記号は集合での記号です。区別するのも面倒なので、以下でも同じに書きます。
x が式(33)の左辺に含まれる原子とすると、

となる。これから、

が出てくる(読者の宿題)。
そうすると、 x は f ( y ) に含まれるか、または f ( z ) に含まれる。
したがって、
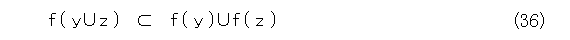
が成り立つ。逆向きの包含関係も同様なので、読者の宿題として、式(33)が成り立つ。
f の定義から、 x を原子とすれば、以下が成り立つ。

ここで、

を原子全体の任意の部分集合とすれば、
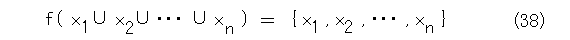
が成り立つ。
次に、任意の y に対して、式(25)を使えば、

の成り立つことが簡単に確かめられるので読者の宿題。
ド・モルガンの法則を使えば、もう1つの演算に対することも出てきます。ということで、残りは、 f が1対1であることのみですね。
任意の原子の部分集合を、

とすれば、

が逆像になるので、全射。
単射であることは、
もし、

とすると、 y が z より小さくならないか、 z が y より小さくならないかのどちらかになる。どっちでも同じなので、 y が z より小さくならないとする。
そうすると、

となる。このとき、

となる原子 x が存在する。この x は y より小さく、かつ、 zc より小さいので、
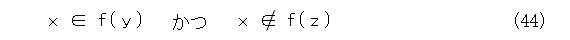
すなわち、

となって単射。
こうして、有限ブール代数は、原子の全体がつくるべき集合と同型になりました。このとき、原子全体の個数を n とすると、このべき集合の要素の数は、 2 の n 乗です。ついでに、有限ブール代数の要素の数は 2 のべき乗しかあり得ないことまで解りました。
6.ストーンの定理
有限ブール代数ではお釈迦様の掌から外へ出られませんでした。それならば、無限ブール代数ではどうでしょうか。まず、無限集合が相手では、原子が役に立ちません。原子の存在しないブール代数があるからです。(あえて例を挙げろとは言いません)
有限集合では、「そんなの有限回で終わるでしょ。」という論法が使えましたが、無限集合では使えません。それに代わる論法を考えるところから始める必要がありそうです。
まず、読者は、「とにかく有限回で終わるならいいや。」と思っているでしょう。少しかっこよく書くと、有限回の操作で完結するものは受け入れるということです。
でも、どっかの国のどこかの会社の管理者は、有限回の操作で完結するからということを認めていません。管理者が部下に、「いつ終わるか解らんものは仕事をしたことにはならん。」とか言って、いつまでに終わるか予定を立てさせています。つまり、「有限の操作で終わる」というよりも、もっときつい論理として、「いつ終わるかが解るもの」だけしか認めていないということです。
ちなみに、この管理者は、部下が不測の事態を考慮して立てた計画に文句をつけ、期限を縮めて再検討させ、さんざん文句をつけた上に、この無謀な期限を守れないと、対策レポートを提出させていました。こうして次の仕事も遅れます。まあ、よくある話ですけど。
ということで、完結するということは、有限回の操作で終了するだけではなく、それがいつ終わるか評価できなくてはならないと考える人もいます。
こう考えてくると、「どこまでの操作を完結したと受け入れられるか。」の問題と捉えられます。無限に対する操作の例として、ゼノンのパラドックスを考えてみましょう。
ゼノンのパラドックスというのは、カメと、アキレスとかいう足の遅いおっさんの駆けっこです。通常、カメは足が遅いことの象徴として使われています。車を運転しているときに、「なにトロトロ走ってんだよ。カメの方がよっぽど速いぞ。」と言ってる人がいますよね。そして、アキレスは、その足の遅いカメのたった2倍の速さでしか走れない鈍足です。
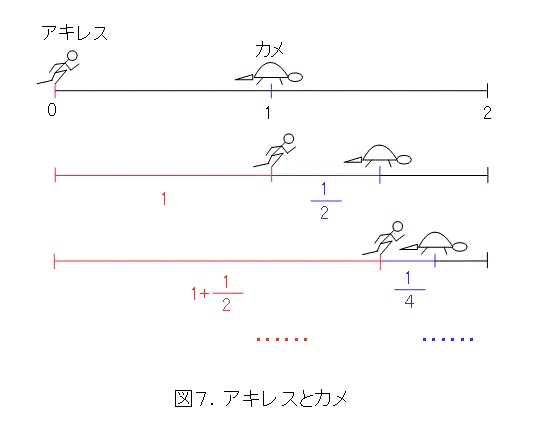
アキレスの駆ける速さを1として、カメの速さを1/2としましょう。アキレスとカメは1直線上にいて、カメの方が1だけ離れています。両者は、「よういどん」で、右へ向かって走ります。
アキレスが、最初にカメのいた位置、つまり1だけ進むとカメは1/2だけ進みます。次に、アキレスがそのカメのいた位置まで進むと、カメは、更に1/4だけ進みます。以下同様で、無限の操作を行うため、いつまで経ってもアキレスはカメに追いつけません。これが、通常、言われているゼノンのパラドックスです。
でも実際は、アキレスがカメに追いつきます。で、これを説明しろという問題が試験に出たりします。この回答で、級数の和を求めたり、測定時間が短くなっている(これも級数の和と同じ)というような回答を書くと、点数は、100点満点でマイナス無限大となったりするので要注意です。もっとも重要な点を見落としていることに気づいたでしょうか。
その前に、この問題で、アキレスは非常に足が速く、常人の10倍以上という話もあり(100メートル1秒以下なのでオリンピック選手なぞ問題になりません)、それが、カメのたった2倍というのは、体調が悪いことを示している。したがって、アキレスは途中で「突然死」してしまいカメに追いつけない。という回答もあります。この回答は、「こりゃ、一本取られたわい。」と評価され、100点満点で120点だったりします(ウソ!)。
それはともかく、アキレスがカメに追いつくのも、級数の和が求まるのも、無限の操作が完結するためと捉えられます。この点が見落とされている点です。もし、無限の操作が完結するということを認めなければアキレスはカメに追いつけません。例えば、コンピューターを使って、カメの位置とアキレスの位置を計算して、それを画面上に表示する(しかも、毎回、画面を長さで2倍に拡大する)ということを考えましょう。明らかに完結しませんね。
ということで、ゼノンのパラドックスは、「無限の操作が完結する。」ということを受け入れるための取り組みと捉えられます。もちろん、無限の操作は完結するものばかりではありません。
以上から、無限について扱うには、無限の操作を完結したとして受け入れられるものが必要です。そこで、今回はツォルンの補題を受け入れることにします。(まあ、それと同値な、選択公理や整列定理などでもいいけど)
ツォルンの補題は、「順序集合の、任意の線形順序部分集合が上界を持てば、その集合は極大要素を持つ。」というものです。
ツォルンの補題については書いてある通りなので、特に、説明の必要もないでしょう。問題は、どうやってこの形に持って行って使うかです。
さて、有限集合では、原子が重要な役割を果たしました。しかし、無限集合では、必ずしも原子が存在するとは限りません。では、なるべく原子に近いものを考えて何とかできないかを調べてみましょう。(式(25)みたいなものが成り立たないかなという意味)
とりあえず図を描いてみます。( a が原子であればいいなー、と思って描きましょう)
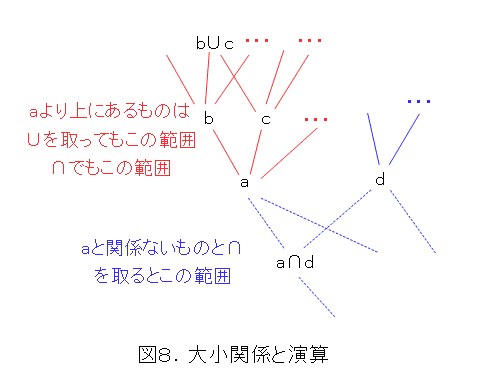
a より大きいところと、小さいところで考えます。 a より大きいところで図のように演算を行うと、必ず a より大きくなり、図8の赤い実線のようになります。一方、 a と無関係なものを持ってきて図のように演算を行うと、 図8の青い点線のようになります。そして、とりあえず a を取っただけなので、 a 自身を使わない記述として考えるのが自然でしょう。
こうして、イデアルの概念に到達します。
Xの空でない部分集合Iが次のイデアルの性質を満たすとき、Iをイデアルと呼びます。正確にはこれ。

イデアルの性質

ついでに、この双対概念がフィルターです。本稿では、フィルターを使いません。
原子に代わるものとして、イデアルを定義しましたが、何から何まで同じというわけではありません。しかし、とにかくイデアルを基に考えて行きましょう。
ここで、Iが 1 を含むとX自身になってしまって面白くありません。それで、 1 を含まないイデアルの方へ目を向けましょう。ただし、イデアルは 0 を必ず含みます(読者の宿題)。
1 を含まないイデアルの全体Aを考えます。この集合A(包含関係が順序)を使ってツォルンの補題の使い方を練習しましょう。やるべきことは、Aの任意の線形順序部分集合Bに対して、Bの上界の存在を示すことです。
こう書くと、よく、やり方が解らないとかなんとか言う人がいます。そういう人の多くは自分自身で動いていないようです。初等幾何のパラドックスのときもそうでしたが、自分自身で動いて作図をすれば、何がおかしいかが解るはずです。その上で理論付けを考えてほしいものです。
今回の場合、自分自身で動くというのは、とにかく例を作り、書いてみることです。
実際、適当に線形順序付けたイデアルの列を書いてみれば明らかです。
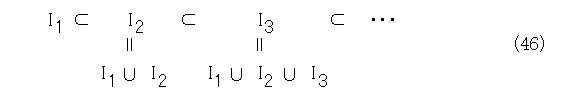
式(46)を見れば、Bの要素であるイデアル全体の合併集合Kをとれば上界になりそうだと予想が付きますね。後は、このようにして作った集合が、イデアルであることを示せばよいわけです。そうすれば、Bの上界になります。
最初に、 1 を含まないイデアルの全体がAであったから、当然Bも 1 を含まないイデアルの集合になります。その合併は当然 1 を含みませんね。
次に、 x 、 y をKの任意の要素とすると、それぞれ、 x 、 y を含むBのイデアルI、Jが存在します。Bは線形順序なので、IがJより大きいか、JがIより大きいかのどちらか。どっちでも同じだから、JがIより大きいとすると、以下が成り立つ。

同様にして、 x をKの任意の要素、 a をXの任意の要素とすると、以下が成り立つ。

これで、Kは 1 を含まないイデアルとなる。KがBの全ての要素より大きいのは、作り方から明らかなので、結局、Bの上界になる。
以上を基に、ツォルンの補題を使って、Aは極大要素を持つことが解ります。この極大となるイデアルのことを極大イデアルと呼びます。
どんどん進みましょう。 1 を含まない任意のイデアルIが与えられたとき、Iを含むAのイデアルの全体Cを考えれば、Iを含む極大イデアルの存在が示せます。当然、読者の宿題です。
更に、Xの 1 でない任意の要素 a に対して、 a を含む極大イデアルが存在します。これは、 a より小さい要素の全体がイデアルになることから示せます。読者の宿題です。
さて、元々イデアルは原子の代わりとして考え始めました。それならば、極大イデアルの方が、より原子に近いのではないかと期待できそうです。つまり、「式(25)みたいなことが出てこないかな」ということです。極大イデアルは集合であることに注意して、形式的に式(25)を書き直してみます。つまり、 1 を含まない極大イデアルIと y を任意の要素として、
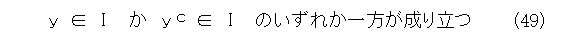
と書けます。
これが成り立つかどうかを調べましょう。
最初に、

となり、イデアルIの仮定に反するので、式(50)はありえない。
そこで、 y がIに含まれないとしよう。
また、

となる任意の x と、Iの任意の要素 a に対し、

となる形の要素の全体を、Yとおく。
v 、 w を y より小さい任意の要素、 b 、 c を Iの任意の要素、 d をXの任意の要素とすれば、
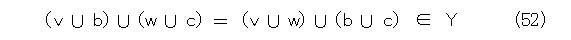
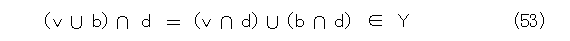
となるから、Yはイデアルになる。
さらに、 a をIの任意の要素、 x を y より小さい任意の要素とすれば、

となって、IはYに含まれる。
ここで、

となり、また、Iは極大イデアルなので、Yは 1 を含むイデアル、つまりX自身になる。ということは、Xの任意の要素は、適当に y より小さい要素 x と、適当にIの要素 a を取って、式(51)の形に書くことができる。特に、Iの要素 b を適当に取って、

とできる。このとき、
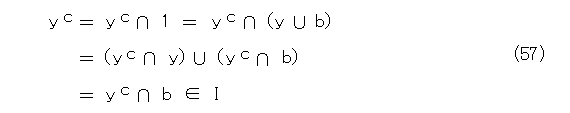
となり、式(49)は成り立つ。
式(49)が示せたので、式(25)と見比べてみましょう。包含関係と、帰属関係の違いはあるけれども、向きが逆です。このことから、双対関係に近い性質を持つと予想されます。なお、全てにおいて、予想を立てるのは重要です。これは、予想が当たっているかどうかではなく、予想を立てること自体が思考訓練として重要という意味です。
では、双対関係に近いとして予想を立てましょう。
有限ブール代数の際に、原子を使った推論で、「原子の拾い出しをやりましょう。 y より小さい原子全体の集合を f ( y ) とします。」ということをやりました。双対関係に近いと考えて、この部分は、「 yc を含むイデアルの極大イデアル全体の集合をF( y ) とする。」と考えられます。そして、同型写像(値域は y をX全体について動かしたときのF( y ) 全体の集合族)になると期待して、演算を保存するかどうかと、1対1になるかどうかを考えましょう。
演算を保存するかどうかにあたって、双対に近いとの期待があるため、有限の場合とは双対の演算について調べた方がよさそうです。つまり、
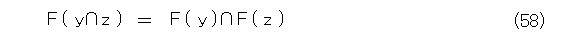
が成り立つかどうかを調べます。
もし、

ならば、Iは、

を含む。Iは極大イデアルなので、 yc か zc のどちらか一方でも含まなければXになり、極大性に反する。したがって、Iは両方とも含む。
これから、IはF( y ) 、F( z )に含まれる。逆の包含関係も同様にして示せるので、読者の宿題。
以上で、式(58)は成り立つ。
次に、以下の式が成り立つことを示す。

IがF( yc )の要素とすると、Iは ycc ( = y )を含む。これから、IはF( y )に含まれない。したがって、IはF( y ) c に含まれる。逆向きは読者の宿題。
以上で、式(60)は成り立つ。
式(58)と式(60)が成り立てば、ド・モルガンの法則によって、残りの演算が成り立つ。
こうして、演算を保存するということが示せました。残りは1対1です。
まず、最初から値域全体に制限しているので全射です。単射の部分だけ確かめましょう。
とりあえず、

とおくと、 y が z より小さくないか、 z が y より小さくないかのいずれかなので、 y が z より小さくないとする。このとき、

となって、

となる。これから、

を含む極大イデアルIが存在する。Iは極大だから、 yc と z の両方を含む。したがって、
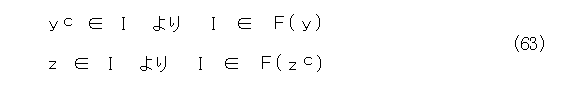
となる。これは、IがF( y )には含まれるが、F( z )には含まれないことを意味する。つまり、

を意味する。以上をまとめると、
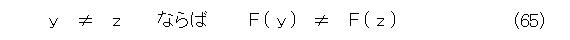
が成り立ち、1対1であることが示せた。
ゆえに、無限ブール代数は、極大イデアルの集合(極大イデアル全体の集合ではなく、その部分集合)に同型であることが解りました。
結局のところ、無限ブール代数を持ってきても、お釈迦様の掌から外へ出られませんでした。これは一例ですが、抽象化しても、結局のところ、世界が広がらなかったということはよくあります。
7.おわりに
今回は、少し難しいことに挑戦してみようと試みました。内容を難しくするのではなく、予想を立てて、それを確認するという方向での実験でした。このようなことは、今までの作品の中でも行っていましたが、今回はかなり明示的に行いました。
内容的には、必要な概念は説明し、集合について基本的な取り扱いを知っていればよいように配慮したつもりです。ただ、問題が少しあり、記号と、色々な文字が使えず、使えても文字化けするという現象に苛まれ(さいなまれ)ました。花文字を使って集合族であることを解りやすくするなどの手法が使えず、かなりごちゃごちゃして解り辛くなった部分もありました。
理科好き子供の広場は、あくまでも知的好奇心の実験場であり、結果や原稿が完全であるとは限りません。実験して、その結果からなにがしかのものが得られればよしとしています。そして、それは、必ずしも読者を対象にしたものではなく、著者自身についてもです。今回の実験がうまく行ったかどうか、現時点では不明です。
また、以前から問題となっていた点として、予備知識をどこまで仮定してよいかということがあります。あまり仮定しない方がよいのは当然ですが、それでは説明がやたらと長くなり、本編に入るまでに飽きてしまいます。そのため、今回、簡単なことや同様にできることは読者の宿題としました。これも一つの実験です。これらの点について、本稿を読まれた方はどうお考えでしょうか。
完
平成28年10月15日
著作者 坂田 明治(あきはる)
|