|
第101話
行列の積を測定しよう
|

「主な対象読者」
今回は行列のことを勉強した人が対象です。具体的には、行列の積が非可換であるという事実から、これを身近な現象や、実験・測定などで感じ取ろうという人たちです。
本 文 目 次
1.はじめに
2.服を着る代数
4.おわりに
著者 坂田 明治
第101話 行列の積を測定しよう
1.はじめに
今回は簡単な話にしようと思います。まあ、「激ムズでいーから。」といってた人からは、なんの反応もありませんし。こいつ、まだ激ムズまで行ってないのに破綻したかな。
さて、今回は行列の積について考えましょう。行列の積を学んだときに、「なんだ、この変態積は。」と思った人もいるのではないでしょうか。行列の和とスカラー倍は成分ごとなのに、積だけ他の成分とのごちゃまぜになっています。この、定義を見て、なんの疑問も無く受け入れる人は何を考えているのでしょうか。
一応、行列の積がごちゃまぜになっている理由を、ちょっとだけ解説しますね。
式(1)は普通の式ですね。少し詳しく書くと、( x , y ) から ( u , v ) への 1次変換(線形変換ともいう)になっています(各変数について1次なのが名前の由来)。

これを、式(2)のように書くことにします。

こうすると行列の変態積は必然の結果となって出てきます。まず、式(2)に式(1)を代入しましょう。
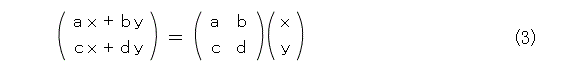
すると行列と列ベクトル(これも行列)の積は、やっぱり変態的に、「かけて足す」という形になります。
更に、式(4)の1次変換を導入して、それを行列表示し、式(2)を代入すると、

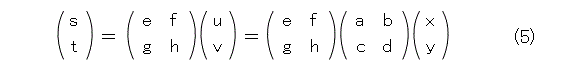
となります。
成分を比較して、
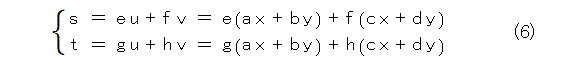
まとめると、
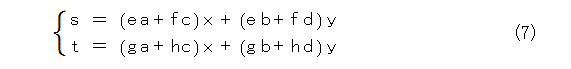
ということで、行列表示にして式(5)の行列部分を比較すると、
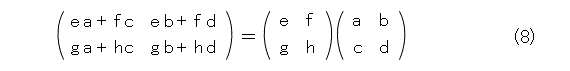
と変態積が出てきます。よく、以下のような模式図が書かれています。

これ、矢印の始点どうし、終点どうしをかけて、その結果を足すと説明されています。
2.服を着る代数
先へ進む前に、ちょっと寄り道をしましょう(いつものことですね)。
行列の積は非可換です。そのため、「なんか、馴染みがない。」とか、「よく解らん。」とかいわれています。しかし、実は、非可換な現象を日常的に経験しています。ただ、あまりにも日常茶飯事なため、それを認識していないようです。
服を着る現象を考えましょう(ただし上半身のみ)。と、こういうと、すぐに、「じゃ、手袋やマフラーはどうなの。」とか、「さらしは。」とかなんとか。さも、鬼の首でも獲ったかのようなケチをつける人がいますね。このような人達は、あくまでも、ここで考察することは一例だということを考えていません。そういう人のいることも考えに入れて、「都合のよい仮定の下で考察します。」と付け加えておきましょう。この、理科好き子供の広場でも、何度もこのような仮定を付けて考察してきましたね。それは、このような理由からです。
さて、本稿を読まれている方は、服を着るときは、下着を着てから上着を着ていると思います。そして、脱ぐときは、上着を脱いでから下着を脱いでいることでしょう。
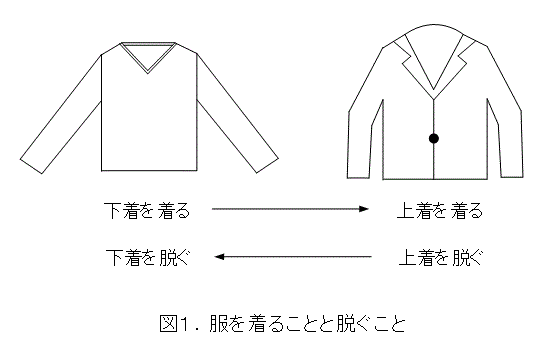
上着を着てから下着を着たり、下着を脱いでから上着を脱ぐ人は、まずいないでしょう。やってやれないことは無いけれども、服を破いてしまったり、体があっちこっち痛んだりして、ろくなことにはなりません(しかも、叱られる)。こういうことはしない方がよいと思います。一応、ここでは禁止です。
まあ、それはともかく、服を着ることを考えましょう。a という服を着ることを単純に a と書くことにします。そして、b という服を着ることを単純に b と書くことにします。そして、a b と書いたときに、「 a を着てから、b を着る。」と解釈しましょう。図1の例では、a を下着、b を上着として、「下着を着てから、上着を着る。」ということになります。明らかに非可換ですね(着る順序を入れ替えられない)。
では、脱ぐときはどうでしょうか。d を脱ぐことを d -1 と書くことにします。他も同様です。もちろん、 d -1 e -1 と書いたときには、「 d を脱いで、e を脱ぐ。」と解釈します。そうすると、「 a b を脱ぐ。」というのは、( a b ) -1 と解釈されますね。
ここで、再び図1をよく見ると、「 a b を脱ぐ。」というのは、「 b を脱いで、a を脱ぐ。」ということになります。つまり、式(9)が成り立ちます。

このように、非可換の積の逆は積の順序が入れ替わります。
この他に、「何もしない。」ことを 1 と書くと、これが単位元になります。また、二枚重ねて着ることを考えると、結合法則の成り立つことが解ります。簡単なので、自分で考えましょう。
なお、非可換な積は、服の脱ぎ着で表されるので、考えに詰まったら、服の脱ぎ着を考えてみるのもよいかと思います。
3.行列の積と電気回路
ここでは、行列の積を手軽に実験・実測することを考えます。行列の積が解りにくい原因の一つは、日常生活と結びつかなかったり、実験と結びつかないことなどです。
そこで、ここでは簡単に作れる電気回路によって、行列の積による予想を実測する実験を考えましょう。必要なものは、半田こて、半田、抵抗器(抵抗値は趣味で決めてよい)、スズメッキ線などの線材(空中結線するなら被覆のあるやつ)、万能基板(なければ空中結線)、テスター、スイッチング電源などです。スイッチング電源が手に入らないときは、電池ホルダーと電池を使用すればよいと思います。
まず、図2の基本形を用意します。これは万能基板にスズメッキ線を2本張っただけです。以下、絵を見て、自分で都合のよいように回路を自作してみましょう。
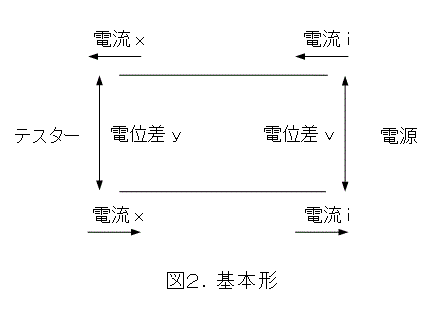
右側に電源を接続し、左側からテスターで電流と電位差(電圧)を測ります。ここで、電流 i と、電位差 v との対を考えましょう。電流も、電位差も、ともに、重ね合わせができますし、スカラー倍もできますので、この二つを縦に並べたものは列ベクトルになります。ここから先、回路を考えて行きますが、1次変換になっている回路(線形な回路ともいう)だけしか扱いません。
まず、図2の場合、式(10)が成り立ちます(実際にはスズメッキ線の抵抗があるのでちょっとずれる)。なお、以下、右に電源があり、左にテスターがあって、そこで測定するとします。必ず、実験誤差を念頭に置きましょう(つまり、理論とぴったり一致しなくても許すということ)。

これを行列表示にすると、式(11)となります。

まあ、とにかく、回路を自作して、測定することをお勧めします。
次に、図3のように、抵抗器を半田付けします。抵抗値はなんでもよいので、適当に選びましょう。図3では、a オームとしておきます。
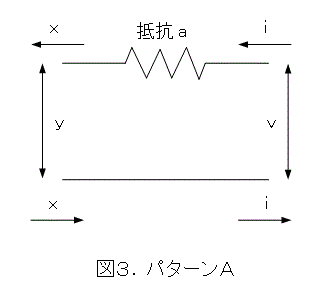
ここで、オームの法則を使って、抵抗値の前後で電位差を求めます。この際に、電流と、電位差(電圧)を、以下のように考えるとよいかと思います。
電気の流れを川の流れとみなしましょう。そこで、電流を「流れる水量」、電位差(電圧)を「流れる水の圧力(勢い)」と考えましょう。すると、図3の抵抗器のある方の線で、川の流れる水量は変わりませんから、電流は変わりませんね。つまり、x = i です。
次に、抵抗器を通るということは、障害物が沢山あって、圧力が打ち消されると考えましょう。コーヒーを入れるとき、お湯がコーヒーフィルターを通ると勢いを失うことだと想像してみましょう。注ぎ込むお湯の勢いより、出てくるコーヒーの勢いの方がかなり弱くなっていますよね。こうして、抵抗器を通ると、電位差(電圧)が下がるということが解ります。このときにオームの法則より、「電位差=抵抗値*電流」となり、この電位差が電圧の降下分ですので、y = v - a i となります。
以上から、式(12)が成り立ちます。

これを行列表示にすると、式(13)となります。

理論と合ってるかどうか、是非、測定してみましょう。
また、式(14)のようにおくと、式(15)となります。
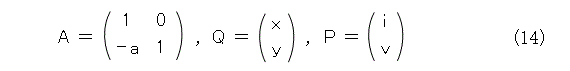

今度は、図4のように抵抗器を半田付けします。もちろん、抵抗値はなんでもよいので、適当に。ここでは、 b オームとします。
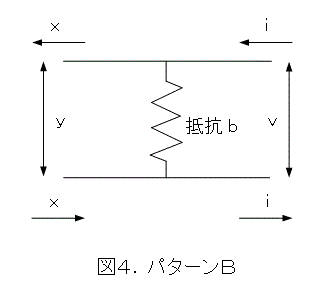
この場合、図4の上の線から、下の線へ電流が流れるので、その分をオームの法則から出します。どの位流れるかというと、「電流=電位差/抵抗値」です。流れた分、電流が減るので、x = i - v / b です。
電位差の方を考えると、左から右へ直接つながっているため、左から加わった圧力は、そのまま右にかかり変化しません。つまり、y = v ですね。
以上から、式(16)が成り立ちます。

これを行列表示にすると、式(17)となります。
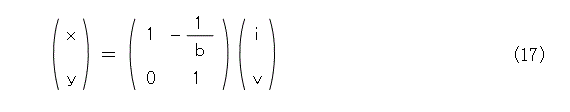
式(18)のように置くと、式(19)となります。


ここから先、入りきれなくなるので、横の線の長さを短めに書きます。実験するときも、やたら長いと面倒なので適当にしましょう(大概、スズメッキ線の抵抗値は、誤差の範囲に入るので無視できる)。
さて、図5のような回路を作りましょう。
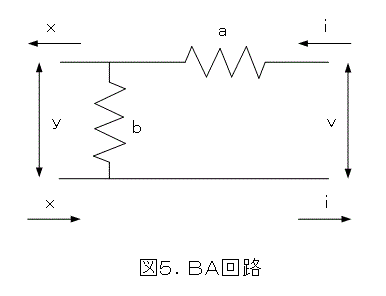
この回路は、Aパターンの左にBパターンを置いたもので、Aで変換した後、Bで変換したものになっています。つまり、式(20)となります。

BAを計算すると、、式(21)となります。
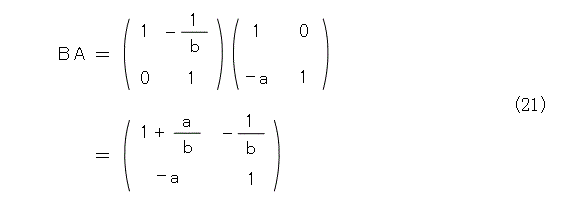
当然、理論値が解ったので、実測してみましょうね。
更に、図6のような回路を作りましょう。
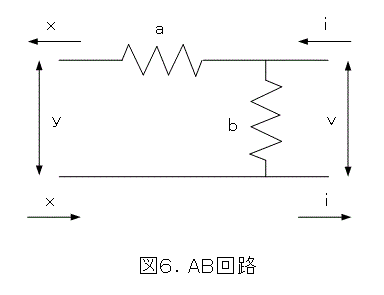
こちらは、先ほどの式(20)とは変換の順序が逆で、式(22)となります。

ABを計算すると、、式(23)となります。
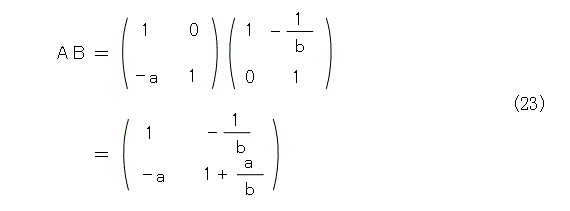
式(21)と式(23)は一致しません。行列の積は交換法則が成り立たないので、当然といえば当然ですね。
そして、図5の回路と、図6の回路で、測定すれば、結果は一致しないことが解るでしょう。つまり、行列の積の交換しないことが、測定によっても確かめられるわけです。是非、回路を自作して実験してみましょう。
おまけです。
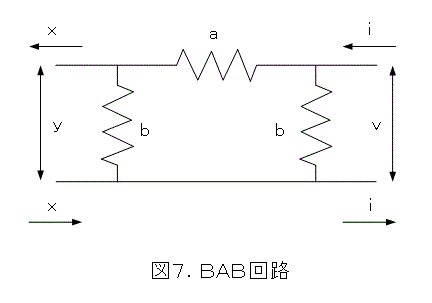
図7の回路は、昔、試験に出たやつです。まあ、まともに考えても出来ますが、今までのことを基にすると、式(24)で計算できます。

4.おわりに
どうも、非可換な積については馴染みが薄いようです。服を着るという現象が、非可換な積になっており、こんな馴染みの濃いはずのものが、どうして認識されないのでしょうか。謎です。
今回は、この馴染みが薄いと思われる非可換な積の代表として、行列の積について考え、実験・測定して感じ取れることを目指しました。
行列の積みたいに変態的なものが天下ってきたときに、何の疑問も抱かずに受け入れるというのはどうなんだろうかと思います。何度も書いていますが、どんなことでも、一応は疑い、「なんでこうなるのか。」を考えてほしいですね。そうして、その現象などが、自分で実験したり、測定して感じ取れるところまで持って行くことができたなら、どんなによいか想像してみてください。この点について、本稿を読まれた方はどうお考えでしょうか。
完
平成30年2月24日
著作者 坂田 明治(あきはる)
|