|
第111話
関数方程式を考えよう
|

「主な目的」
今回は実数から実数への線形変換についての話です。線形変換を関数方程式として扱った場合や定積分の積分範囲の加法性を楽しむものです。
本 文 目 次
1.はじめに
2.線形な関数方程式
5.おわりに
著者 坂田 明治
第111話 関数方程式を考えよう
1.はじめに
今回は、関数方程式について考えてみましょう。
関数方程式なんて書くと、面倒で、さんざん苦労した上に解けなかったとか、そんな悪夢がよみがえります。面倒なことはしたくないので、線形変換の式を関数方程式とみて、これを扱いましょう。
とりあえず、実関数で考えます。なお、いつものことですが、都合よく扱える状況や変数などを一々細かくは書きません。それらは自分で考えて補いましょう。
2.線形な関数方程式
最初に扱うのは線形変換の式です。


これを解くには、どうすればよいでしょうか。式(1)をよく見れば、 x と k の関数になっています。2変数なので、まず、どちらか一方を固定し、1変数の関数とみなして考えるのがよさそうです。固定するときに、変数が見えると目がくらむため、簡単な値に固定して試してみましょう。
最初に、 k を1とおいてみると、何も出ませんね。

次に、 x を1とおいてみます。

これではかっこ悪いので、 k を x とおきましょう。

更に、 f ( 1 ) を a とおきます。

要するに、式(6)の1次関数が解です。これは、式(2)を満たしています。つまり、1次元では式(1)は式(2)に吸収されてしまいます。やはり、
式(1)、式(2)の両方が必要になるのは2次元以上ですね。そのときは、線形変換が行列になります。念のため、自分で確かめてみましょうね。
そこで、式(2)から式(1)が出るでしょうか。つまり、式(2)の解は1次関数になっているかが気になりますね。
3.線形変換の加法部分の関数方程式
式(2)を解くには、どうすればよいでしょうか。見当が付かないときは、色々と試してみるのが常道です。
まず、式(2)で y を x とおいてみます。

これは、式(1)で、 k が2の場合です。同様にして、 k が n の場合は次のようになります。
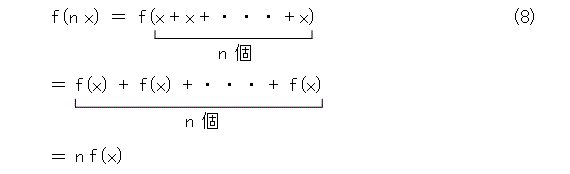
つまり、 k が正の整数の場合は式(1)が成り立ちます。更に、式(8)を利用して、式(9)が成り立ちます。
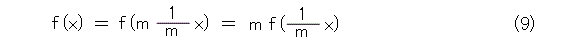
これから式(10)が成り立ちます。

そうすると、式(10)と式(8)によって、式(11)が成り立ちます。

つまり、 k が正の有理数の場合に成り立つことが解かりました。これを有理数全体に広げましょう。まず、0の場合です。
式(2)で、 x と y を0とおいてみます。

これから式(13)が出てきます。

したがって、式(14)が成り立ちます。

今度は、式(2)で y を - x とおきましょう。
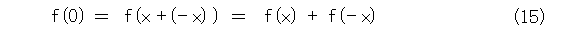
そうすると、式(16)が出てきます。

負の符号は外へ出せるのが解かりましたから、今までのことを総合して、有理数 r について式(2)が成り立ちます。

ここで、もし、 f が連続であれば、実数へ収束する有理数列をとることによって、式(1)が成り立ちます。しかし、一般的に、 f は連続とは限りませんので、式(2)から式(1)は出てきません(不連続の場合、式(6)のような解にはなりません)。
以下、式(2)の不連続な解の話です。ぐっちょんぐっちょん、どろどろの話なので、興味のない人は飛ばして、第4章へ進みましょう。書き方はテキトーなので、興味のある人は精密に組み立てなおしましょう。
まず、実数は有理数体上の無限次元ベクトル空間です。ベクトル空間であるというのはよいでしょう。次元が無限であることは、有限次元とすると、実数が可算濃度になってしまうからです。ちなみに、実数のことを連続濃度ともいいます。濃度の話は、その内するかも知れません(気が向いたら)。
このとき、実数には基底が存在します。これはツォルンの補題から示せます(当然、読者の宿題)。そうすると、基底から有限個のベクトル(ここでは基底ベクトルと呼ぶことにします)を選んで、任意の実数は以下のように書くことができます(ちなみに、基底ベクトルは実数)。

そうすると、今までのことから、式(19)のようになります。

当然ですが、一般的に、式(19)の基底ベクトルは、式(18)の基底ベクトルとは別物です。その上で、実数 k と x の積は、式(20)のようになります。

もちろん、一般的に、式(20)の基底ベクトルは、式(19)の基底ベクトルとも、式(18)の基底ベクトルとも別物です。つまり、一般的に、式(19)と、式(20)は異なります。すなわち、式(1)は成り立ちません。
4.加法的な関数方程式
今度は、式(21)の関数方程式を考えましょう。確かに加法的ですが、なんか難しそうですね。
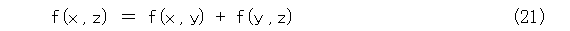
全然、見当も付かないので、あきらめましょう。と、最初に投げることを考えるのは、いつものやり方です。
一応、あきらめないで式をよく見ると、 x から、 z までが、 x から y までと、 y から z までの和になっています。これ、見たことあるでしょう。図1のような面積の計算ですね。
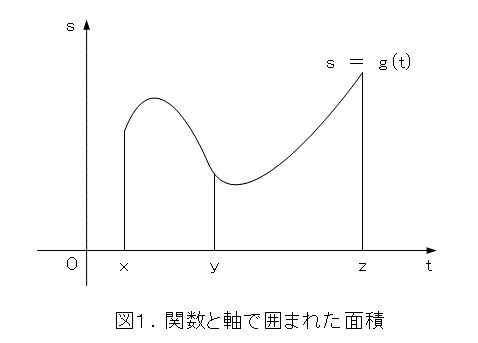
そうすると、式(22)のようなのが例になっています。
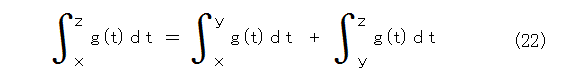
よく解かりましたね。じゃー、式(21)を解きましょう。(こんなの本当に解けるのか。どうせまた、途中で手抜きして、解けたことにするんじゃないのか。)
例として、定積分が出てきたので、定積分のことを考え直しましょう。定積分の計算方法は、 g の不定積分を G として、式(23)のように計算できます。
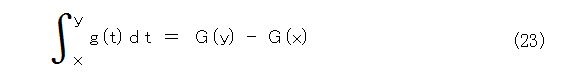
この式を、不思議な式だと感じた人も多いかと思います。定積分って、面積でしょう。それが、不定積分の端の値だけで決まってしまいます。なんか、評価が、途中の努力に関係なく、最初と最後だけで決まってしまうような感じで、とても嫌な気分になりますね。まあ、それが現実なんだろうけども。
さて、一般的に不定積分なんて求まらないから、式(23)は、 G がなんだか解からなくても、解かったことにして、計算できているとしています。それならば、きっと、式(21)もなんだかよく解からない関数を、解かったことにして、同じように解が求まると期待できるでしょう。この方針でやってみます。
式(21)を変形して、式(24)を得ます。
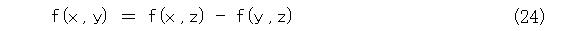
左辺は z に関係ない、つまりどうでもよいから、 z をある特定の値 a に固定しましょう。
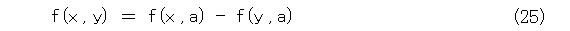
その上で、 f (x , a) は x だけの関数と考えてよいから、式(26)のようにおきます。

式(26)を式(25)へ代入して、式(27)が得られます。

めでたく、式(21)は解けましたね(こんなんでいいのか)。この式を見ると、関数は、差分の形をしていることが見て取れます。そうすると、式(21)は、途中が何であれ、途中の部分は打ち消しあってしまいます。最初と最後で決まってしまうというのは、こういうことだったのですね。
5.おわりに
線形変換を関数方程式とみたときに、加法に関する関数方程式は、結構複雑な問題をはらんでいました。こういう、一見簡単そうに見えて、実は複雑な問題を抱えていることはよくあります。その一方で、第4章で扱った加法的な関数方程式のように、複雑になるかと思いきや、案外簡単に扱えて、しかも、中間部分が寄与しない理由まで解かってしまうという例もあります。それ故、とにかくやるだけやってみて、よく考えることは重要でしょう。
よく、ものごとを進める上で重要なのは、分析力と統合力だといわれます。確かにそう思いますが、どうやって、分析力と統合力を身につければよいのでしょうか。その一つの方法として、理科好き子供の広場では、単なる知識として伝えるのではなく、色々と考えてみようとしています。そうすれば、考えを進める上で、分析力や統合力が身についていくのではないかと思っています。この点、本稿を読まれた方はどうお考えでしょうか。
完
2021年7月25日
著作者 坂田 明治(あきはる)
|