|
第116話
ゼロの比で息抜き
|

「主な目的」
複雑なものを単純化するために、複雑なことを考える一例として、ゼロの比を扱っています。筆者は、今回の内容を「息抜き」と称していますが、実際は「手抜き」です。
本 文 目 次
1.どうでもいい話
3.ゼロの比を考える
4.2直線の平行条件
5.比の定義
著者 坂田 明治
第116話 ゼロの比で息抜き
1.どうでもいい話
暑い。暑過ぎる。こんな暑いのに、ビンボをなんとかしないと。ビンボっていうのは、第113話で出てきた、通称ビンボウカズラこと「ヤブガラシ」だ。こいつら、根を獲っても獲っても、根を枯らす除草剤をかけても、ゾンビのように次から次へと生えてきやがる。まさにゾンビ草だ。
春から、ビンボが生えてくると、根を掘り出して獲っていたが、獲りきれなかった。大体、根を切らないで全部獲るなんてできっこない。どうしても掘り出しきれず、途中で切れてしまう。それに、この根の太いのなんのって、長薯か自然薯みたいにぶっとくて、「一体何年物だ。」と思う程だった。ゴミ袋何枚分獲れたろうか。これが長薯か自然薯だったら儲かったのにな。
まあ、それでも、去年かなり獲ったんだから、今年は、多少、少なくなったんじゃないかと期待したが、逆に増えやがった。しかも成長が異様に早い。今年は暑いからか、それとも、切れて残った根がヤケクソになって芽を出したからか、全然手付かずで残ってた根が一斉に芽を出したからか、こりゃたまらん。
この時期になってくると、ビンボの根が他の植物の根に絡んでいて、というよりも、他の植物の根の間に混ざっていて、根を抜くと他の植物の方が被害を受けてしまう。とにかく、作戦変更で、葉や茎から吸収されて根を枯らす除草剤をビンボにだけかけてみた。確かに、かけると地上部は枯れるが、また、どっかから芽が出てきやがる。しかも、他の植物に多少かかってしまうため、枯らしたくない植物も枯れたり、生育障害を起こしたりしている。
それよりも頭にきたのは、ビンボのせいでアシナガバチに膝と腕を刺されてしまったことだ。こいつら、とんでもない所に巣を作りやがって。大体、膝の高さより下の所に、しかも、見つからないように巣を作っていやがる。以下は去年撮ったアシナガバチの巣の写真。とにかくでかい。

全体が入る様にして撮った写真はこっち。

去年は、こんな巣が4個と巣別れした小さい巣が1個あった。こりゃまずいと思って、業者に駆除してもらったなー。
今年のは、まだ、そんなに大きくなかったけど、見つかりにくいように巣を作りっていて、しかも、巣の近くにビンボがやたらと生えていたため、刺されてしまったではないか。
そもそも、気候変動で、日本が熱帯化しているのに、家の庭をコンクリートやアスファルトで固めたり、砂利を敷き詰めたりして、更に都市型気候を増幅している輩がやたらと多いのが悪い。駆除業者のおっさんの話では、昔、この辺りはスズメバチが3種類だったが、最近では、外来種や南の方のスズメバチが住み着くようになって7種類ぐらいに増えたとか言っていた。もちろん、うろ覚えのため、この種類の数字は当てにならないけどな。
で、アシナガバチは熱帯化の影響で巣が巨大化してると言ってた。巣の直径が30cm位になることもあるそうだ。その上、アシナガバチに刺されてもあんまり痛くないが(誰だ。こんなウソついたの。めちゃくちゃ痛かったぞ。)、同じところを連続で刺す攻撃をしかけてくるとも言ってた。攻撃の仕方も考えているなー。
とにかく、ビンボが悪い。こいつさえ生えてなければ、わざわざアシナガバチの巣の近くに行ったりせず、刺されることもなかったのに。
2.ゾンビ草からゾンビ数へ
という訳で(どんな訳だ?)、ゾンビ草にたいする恨み辛みから、ゾンビ数を扱うことにしました。まあ、息抜きのつもりで楽しみましょう。なお、第15話を参考にするのもとよろしいかと。
第15話でも書いたとおり、 0 は無敵のゾンビです。 0 は加法に対しては全くの無力で、何の効果もありません。

式(1)を見ると、何の生産性も無いということですね。
しかし、積については無敵のゾンビです。

つまり、どんな奴も、 0 をかけると、結果は 0 です。これは、ゾンビにかまれると、死んでゾンビになってしまうということです。そして、このゾンビの存在がやっかいなことを引き起こします(ビンボみたいに取り扱いが面倒になる)。
例えば、「有理数と無理数をかけたらどうなるか。」という問いに、通常は「無理数」と答えるでしょう。つまり、よく見かける式(3)です。

ここでの流れから、もう解かっていると思いますが、式(3)は正しくありません。式(4)の場合が発生します。

こういうことから、一々、場合分けして、ゾンビを例外として扱う必要が出てきます。例えば、第15話で、1次方程式を解くときに、係数がゾンビかどうかを考えていましたね。つまり、式(5)のときに、

の解は、ゾンビの場合分けをして式(6)のようになります。
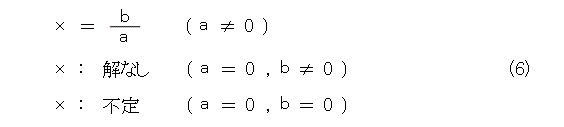
そして、このことから、「 0 で割ってはいかんぞ。」という話が出てきます。小学校以来、とにかく 0 で割ってははならないとか、分母が 0 であってはならないと植えつけられてきました。第15話にも、そんなことが書かれています。
更に、「比も割り算や分数と同じようなものだから、 0 が出てきてはならないと叩き込まれてきました。
ところが、高校辺りでは、いつの間にか、 0 の比を扱うようになります。それも、どっかの国の民主主義みたいに、これに関するちゃんとした理由も説明せず、いきなり導入して、知らん顔しています(第95話でも、知らん顔して使っていたな)。
ちなみに、どっかの国は、民主主義だとか言ってるが、国民が望むような法案は通らず、国民を無視した閣議決定法案が通っていて、政府の信用は地に落ちています。これ、どっかの国の周辺にある権威主義国家とは、程度の差はあれ、どこが違うのでしょうか。民主主義なんて、権威主義とほぼ同じじゃないかと子供たちは見ています。ついでに、「丁寧に説明」というのは、「説明しないこと」、「寄り添う」というのは「ほったらかしにすること」、などなど、勝手に日本語の意味を変えるの止めて貰える。子供たちが見てんだよ。子供たちが。子供は大人が考えてるより敏感なんだよ。どうするつもりなんだ。
そこで、本稿では、 0 についての比を考えましょう。
3.ゼロの比を考える
まず、比について考えましょう。よく出てくるのは線分の比ですね。そこで、線分ABを m : n の比に分ける点をPとします。

次に、Pの位置をベクトルを使って書き表しましょう。
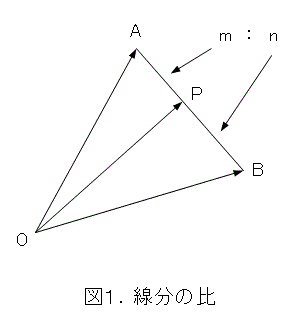
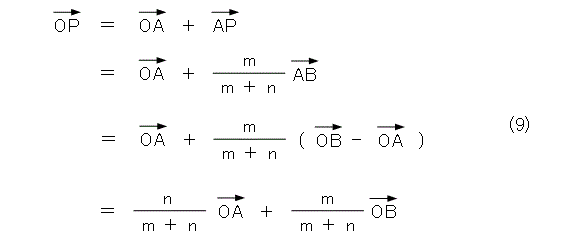
図1のようにすると、線分ABを m + n 等分して、その内の m 個分の位置がPの位置になるから、

となります。
したがって、点Pの位置は、式(9)のように求まります。
ここで、式(10)のように置きましょう。
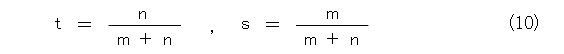
そうすると、式(9)は式(11)、式(12)のようになります。


式(10)から、 m と n の比は、 s と t の比です。
更に、式(11)と式(12)から、 s を実数全体にわたって動かせば、点Pの軌跡は直線ABになります。
ところで、 s = 0 とすれば、点Pは点Aと一致し、このときに、 s と t との比は、 0 : 1 となってしまいます。もちろん、 t = 0 とすれば、点Pは点Bと一致し、このときに、 s と t との比は、 1 : 0 になります。
つまり、 0 の比を考えに入れなければ、式(11)、式(12)は直線を表すことができなくなってしまいます。これでは都合が悪いので、高校辺りでは、こそっと 0 の比を導入して使うようになっていました。
4.2直線の平行条件
今度は、2直線の平行条件を考えましょう。
2直線が図2のような場合は簡単です。
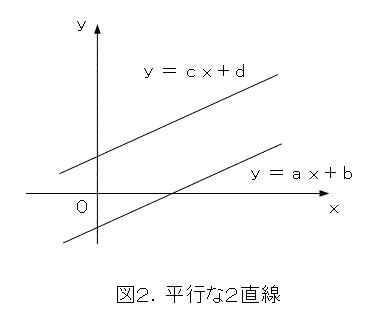
2直線が一致した場合も平行として、平行条件は a = c ですね。この際に、 b と d はどうでもよくなります。しかしながら、図2のような直線の方程式では、 x 軸に平行な直線が表せず、一般的とはいえません。もっと一般的に書き表したものが図3です。
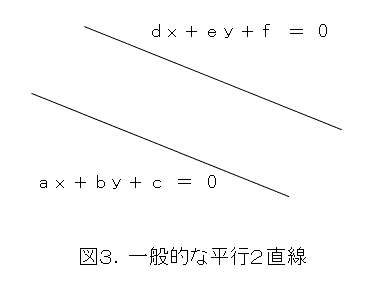
明らかに、 c と f はどうでもよいでしょう。問題は、 x と y の係数です。 b と e がともに 0 でなければ、 y について解いて、 x の係数を比較すればよいでしょう。この際に、平行条件は式(13)となります。

同じことですが、よく、比の形で式(14)のようにも書きます。

もし、 b が 0 ならば、図3の下の直線は、 y 軸に平行な直線となります。この場合、 e も 0 でなくてはなりません。更に、 a と d はともに 0 であってはなりません(そうでないと直線にならない)。このときに、式(14)へ当てはめる(形式的に無理矢理代入する)と、やはり、 0 の比が出てきます。もちろん、 a が 0 のときも、同様です。また、 a と b は同時に 0 とはなりません( d と e も同様)。
前章の線分の比と、2直線の平行条件とから、どうも 0 の比を考えなくては、色々と都合が悪くなってきましたね。
5.比の定義
そもそも、比の定義はどうだったのでしょうか。小中高では、比をなんとはなしに導入していて、ちゃんとした定義をしてなかったような気がします(小中高のことを全然覚えてないのでテキトーに言ってるだけ)。
大体、比例の話を元に、「こう書くんだよ。」とやったような気がします。つまり、 a と b が比例するというのは、適当な 0 でない定数 k を用いて、式(15)のようになることでしたね。

おなじことですが、書き直すと式(16)となります。

また、このことを式(17)のように書きます。

それで、式(18)のように解釈したりします。

まあ、特に、この解釈にこだわる必要はないので、式(19)のように解釈してもほとんど同じです。

以上のやり方では、式(15)で、 a か b を 0 とすると、ゾンビの呪いに遭って、なにがなんだか解からなくなります。
ということで、この方法では無理があるようですね。そこで、キチンとした定義を考えましょう。
まず、線分の比と直線の平行条件を考慮すると、式(12)ならびに、第4章の終わりの方の注意(赤字の部分)から、比では、同時に 0 とはならないという制限が必要ですね。
さて、ここから先、どうしたらよいのでしょうか。高校までで、ちゃんとした定義が出てこないということから、何か、高校まででは扱わない概念を使うと裏読みできます(いいのか、こんなこと教えて)。
とりあえず、文字は全て実数としますが、複素数としても問題ありません。
そこで、同時には 0 とならない、順序付きの2つの数の組を、

と書いて、これを「比」と呼びましょう。もちろん、 a 、 b が共に 0 でないときは、式(18)となることを目指します(式(18)を見る限り、 a が 0 でもいいけどな)。
このままでは、ただの文字列にすぎないので、色々取り扱えて意味を持つように、「比が等しい」ということを導入します。
2つの比、 a : b 、 c : d において、比が等しいということを、式(21)が成り立つこととします。

こうすることによって、比を等しいかどうかで類別できるようになります。更に、拡張して、同時には 0 とならない、順序付きの3つの数の組を考え、

「比が等しい」ということを同様に、
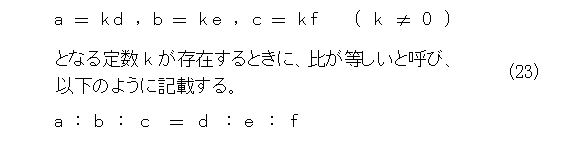
とします。以下同様な拡張ができます。
比については色々な性質が成り立ちます。例えば、加比の理が成り立ちます。
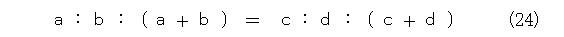
その他にも、比についての色々な性質が成り立ちますが、当然読者の宿題です。
また、2つの数の比に関して、 b が 0 でないときは、式(25)のように対応付けることもできます。

つまり、このように比に分数を対応させても何ら問題は起こりません。特に、a が 0 のときは、比の値は 0 となります( b が 0 とはならないことに注意)。
b が 0 のときは、 a は 0 でなく、式(26)が成り立ちます。

この、 1 : 0 は通常の実数ではない「なにか」です。まあ、結論から言えば、無限遠点です。詳しく知りたい人は、第95話をどうぞ。
とにかく、ゼロの比を考えても、色々な取り扱いができて便利になったので、これでよしとしましょう(これ、本当に息抜きか)。
完
2023年8月1日
著作者 坂田 明治(あきはる)
|