第１１８話

　１０進法表記から数字を取り出す

　

「主な目的」

１０進法の表記について、多少なりとも興味を持っている人が対象です。１０進法の各桁の数字をを求める際に、 10 でコツコツと割って計算するのではなく、ガウスの記号を利用する試みを行います。

　

　

本　文　目　次

　１．どうでもいい話

　２． １０進法表記

　３．ガウスの記号

　４．目的桁の数字の取り出し方

　

著者　坂田　明治

　

　

　

第１１８話　１０進法表記から数字を取り出す

　

１．どうでもいい話

　その昔、カモがツルを襲撃するとか言ってた奴がいたけど、本当かねー。これ、昔の忍者アニメのオープニングで、掟がどうとかのナレーションの際に、カモがツルを襲撃していたのがあって、その影響じゃないのか。大体、カモは種類を問わず群れているしな。この近辺にツルはいないから、よくわからん。まあ、しかし、よくサギと一緒にいるから、襲撃なんかせず、一緒に群れていると思うな。ほら、調整池の岸で撮った写真にも一緒に写っている。

　

　

　実際、カモがサギを攻撃してるところを見たことがない。見かけるのは、ドブガモどうしの追いかけっこだ。どうも仲の悪いのがいるらしく、特定のやつを追い回している。

　

　そうそう、この近辺にはタカもいるし、変な内部抗争してたら、タカの餌食になるんじゃないかな。ほら、電柱にタカが留まっている。

　

　

　タカがカラスを攻撃しているところを見たことがあるけど、全然成功しなかった。見ていて、首が痛くなっただけだったな。

　

　まあ、タカと言えばキジだな。キジは警戒心が強く、逃げ足も速く、見られるかどうかは運しだいだ。

　

　

　せっかく見られても、人間に気づくと走って逃げてしまう。どうも性質がニワトリに似てるらしく、飛ぶよりも走るか歩いている方が多い。

　

　タカとの関係だけど、ある時、キジを見かけて、写真を撮ろうとしたら、急に慌てて、飛んで逃げてしまった。「飛んで逃げるなんて、いくらなんでも、変だ。」と思い、上空を見上げたら、タカが飛んできていた。やっぱりタカは怖いんだ。

　

　ちなみに、キジは縄張り意識が強いらしく、オスが鉢合わせると、頭を下げて威嚇する。偶然この写真が撮れた。

　

　

　頭を下げて威嚇するのは、キジだけじゃなく、カモもよくやっている。ドブガモも頭を下げて追いかけていたっけな。

　

　というわけで（どんなわけだ）、今回は、１０進法表記から、目的とする桁の数字を取り出すことを考えよう。

　

　

２． １０進法表記

　１０進法表記は、普通によく使っているよね。

　

　例えば、 1234 （一千二百三十四）は式（１）の意味です。

　

　

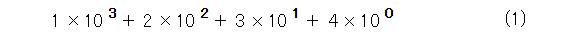
　一般に、正の整数 a は、式（２）のように１０進法表記ができます。その際に、 10 のべき乗の前についている数字を係数と呼ぶことにします。

　

　

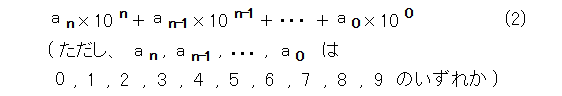
　これ、 a を10で割り、その余りを取り出し、その商をまた10で割り、その余りを取り出しというのを繰り返していけば、式（２）が得られます。また、このやり方から、正の整数 a の１０進法表記は、一意的に定まります。

　

　そうして、正の整数 a と、その１０進法表記は等しいものとみなし、式（３）のように書きます。

　

　

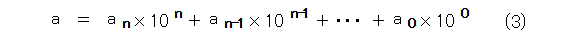
　通常、１０進法表記した数字を扱っていますが、これは表記の一種で、正の整数 a は２進法表記や３進法表記など、色々な表記ができます。そして、それらは表記の違いだけで、同じ数を表していることから、全部等しいものとして扱います（ただし、どういう意味で表しているかの記載が必要）。

　

　ちなみに、１６進法表記では、係数が、 0 から 9 までの数字では足りないので、AからFも数字として使用します。これらはよく知られているので省略。代わりに、日本で昔から使われていた、距離を表す不等進法についてちょっとだけ書きます。

　

　これ、里（り）、町（ちょう）、間（けん）、尺（しゃく）を単位とし、その係数は、知らん顔して１０進法で表します。そして、各単位は式（４）によって換算します。

　

　

　例えば、１里２町３間４尺は、式（５）のようになります（計算結果は当てにしないこと）。

　

　

　次に、正の整数から拡張して、正の実数を考えましょう。

　

　例えば、 1234.567 です。これは、式（６）の意味です。

　

　

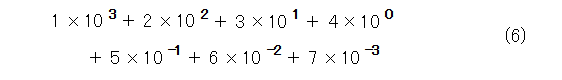
　一般に、正の実数 a は、式（７）のように１０進法表記ができます。この場合も、 10のべき乗の前についている数字を係数と呼ぶことにします。

　

　

　と、ここで、問題が発生します。式（２）は一意的に定まりますが、式（７）はそうではありません。まず、用語を用意しましょう。

　

　通常、式（７）で１の位を、 a₀ 、 10 の位を a₁ など、また、小数点以下では、少数第１位を a_-1 、小数第２位を a_-2 などとしていました。しかし、これだと整数部と小数部で統一性が無く、更に、日本語では無量大数より大きい単位もなく、淨より小さい単位もありません。そもそも、大きくても、小さくても、無限に単位を用意するなんてことはできませんね。

　

　そこで、もっと合理的に位の数を定めます。式（７）の 10 のべき乗で、 10 の肩に乗っている指数をもって位とします。そうすると、それぞれの係数は、 0 の位は a₀ 、 1 の位は a₁ 、 2 の位は a₂ 、 n の位は a_n 、 -1の位は a_-1 、 -2 の位は a_-2 、 -k の位は a_-k となって、きわめて簡潔な表現になりました。

　

　さて、式（７）の表記が一意的ではない例を考えましょう。

　

　例えば、 1 と 0.999・・・（ 9 が無限に続く）です。この両者は、実数の連続性によって同じものになります。

　

　

　こうなると、どんなときに２通り以上の表記が発生するのか気になりますよね。そこで、正の実数 a の表記がもう一つあったとして、それを式（８）とします。このとき、表記によって桁数も合ってない可能性も考え、係数に 0 を補って桁数を揃えておきましょう。当然、式（７）と式（８）は同じ数の表記なので等しくなります。

　

　

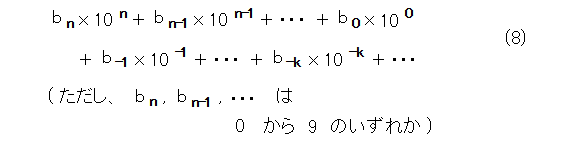
　最高位から、式（７）と式（８）の係数を比較していき、最初に違いが出てくる係数をそれぞれ、 a_i 、 b_i とします。これらは異なるとしているので、 a_i の方が大きいとしましょう。そうして、式（７）と式（８）の係数の差を考えると、 a_i より高位の部分での差はありません（そういうことにしているから）。そうすると、 a_i およびその低位の部分が問題となります。

　

　このとき、

　

　

となります。

　

　ここで、 1 は繰り下げられるが、 2 以上だと余りが出てしまいます。つまり、式（９）の左辺が 2 以上だとすると、余りが出て、式（７）と式（８）は別の数ですね。これから、式（９）は、式（１０）となります。

　

　

　繰り下げによって、次の位の係数の比較は、 10 + a_i-1 と b_i-1 の比較になります。このとき、それぞれの係数は、 0 から 9 までの整数だから、明らかに前者の方が大きい。ここでも 1 しか繰り下げられないことを考えると、

　

　

となります。以下同様です。

　

　そうして、式（７）、式（８）は、式（１２）、式（13）のようになります。

　

　

　

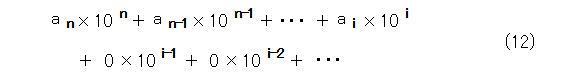
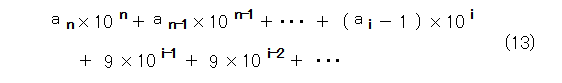
　これで、表記はあっても２通りしかなく、 1 と 0.999・・・と同様の形になりました。

　

　このとき、よく見ると、式（１２）は有限項で打ち切られています。そうすると、有限項で打ち切られるものは、 9 が無限に続く形式の別表記もあるということがわかりました。このどちらか一方を、１０進法表記とするかにあたって、当然、簡単そうな方がよいでしょう。有限項で打ち切られる方が簡単なので、表記が2通りある場合は、有限項で打ち切られる方に一本化します。

　

　これで、正の実数から、指定した位の係数を取り出すためには、その数を１０進法表記にして取り出せばよくなります。今回のタイトルにあることは、これで終了ですね。めでたし、めでたし。（でいいのか）

　

　

３．ガウスの記号

　まあ、高校あたりで出てきて、何に使うかわからない関数の代表格がガウスの記号ですね（ガウスの関数と呼ぶこともある）。

　

　それで、どんなものかと言えば、実数 x に対して、 x を超えない最大の整数を対応付け、それを記号で、 [ x ] と書きます。例えば、 1234.678 に対して、式（１４）のようになります。

　

　

　よく、正の実数に対しては、小数点以下を切り捨てる関数だと言う人がいるけど、それはあまり正しくありません。

　

　

はよいとして、小数点以下の切り捨てだと、

　

　

とやりそうで危険ですね。式（１６）のガウスの記号の中身が 1 と認識していれば、こんな間違いをしなさそうだけど。

　

　こうしてみると、ガウスの記号は、前章でやったように、有限項で打ち切れるものは打ち切るとした表記との相性がよさそうです。このように表記を絞った場合、正の実数の小数点以下を切り捨てたものと言って差支えないでしょう。

　

　さて、式（１４）から、小数部分は式（１７）のように書けますよね。

　

　

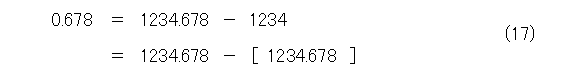
　そこで、実数 x に対して、 < x > を式（１８）のように定めます。

　

　

　これは、正の実数 x に対して、整数部分を切り捨て、小数部分を取り出したものですね。

　

　なお、ガウスの記号に関して、例えば、以下の等式がなりたちます。

　

　

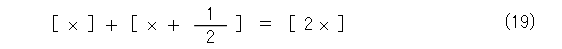
　式（１９）が成り立つことは、実数 x を以下のように分けて考えればすぐにわかります。

　

　

　

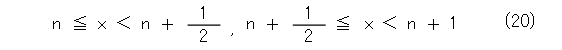
４．目的桁の数字の取り出し方

　ということで、正の実数 x に対して、 [ x ] は小数点以下の切り捨て、つまり、整数部分の取り出し、 < x > は整数部分の切り捨て、つまり、小数部分の取り出しです。これらを使えば、目的桁の数字の取り出し、つまり、指定した位の係数を取り出せそうですね。

　

　そこで、 1234.678 の位が 1 の係数、つまり、 10 の位の数を取り出してみましょう。色々なやり方を思いつきますが、図２で２通りの方法を記載をします。

　

　

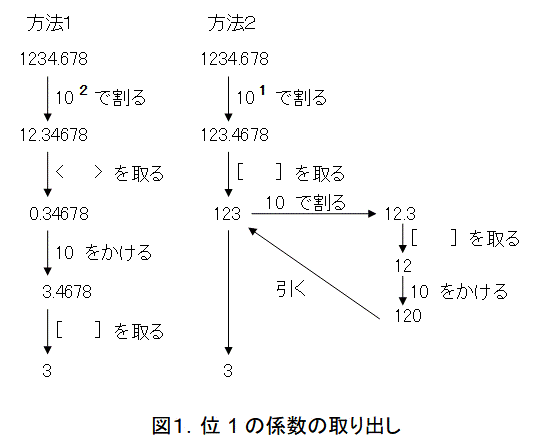
　図2を参考にして、実数 x に対して、位が j （整数）の係数を取り出しましょう。

　

　まずは、図２の方法１を参考にすると、 j 位の項を小数点第１位に落とすため、 10 ^j+1 で割り、次いで整数部を切り捨てます。そして、 10 倍してから小数点以下を切り捨てます。ということで、式（２１）のようになります。

　

　

　次に、図２の方法２を参考にすると、 j 位の項を １ の位に落とすため、 10 ^j で割り、次いで小数点以下を切り捨てます。このときに、 10 の位以上が邪魔なので、これを切り捨てるため、 10 で割って、小数点以下を切り捨ててから、 10 倍したものを引きます。ということで、式（２２）のようになります。

　

　

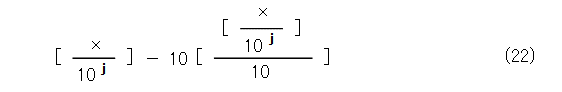
　こうしてみるとガウスの記号も役に立つし、一々１０進法表記にしなくても、求める位の係数が計算できますよね。

　

　

完

　

2024年3月24日

著作者　坂田　明治（あきはる）