|
第95話
鏡の国の光子さん 〜円錐曲線三兄弟の正体〜
|

「主な対象読者」
今回の主な対象読者は「第6話 鏡の国の光子さん その二」を読まれ、円錐曲線三兄弟に興味をもたれた方です。かなり修正し、脚色を加えてはいますが、あるところで実際に行われた勉強会が元になっています。なにがしかの参考になれば幸いです。
本 文 目 次
1.はじめに
2.予備的考察
3.射影
5.接線
7.おわりに
著者 坂田 明治
第95話 鏡の国の光子さん 〜円錐曲線三兄弟の正体〜
1.はじめに
今回は、「第6話 鏡の国の光子さん その二」を読み、円錐曲線三兄弟に興味を持たれた方が対象です。ネットであっちこっちを見ていると、図22にリンクを張っている人が見受けられます。よほど気に入ったのでしょうか。
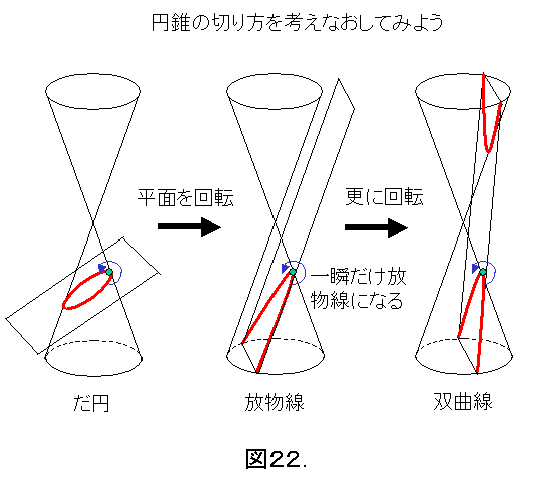
この図の意味するところは、平面を回転させていくと、だ円が、一瞬だけ放物線に変わり、そして双曲線へと変わることです。現象を眺めると、だ円の端がびろーっと無限の彼方へ延びていき、放物線が出現し、その後双曲線になり、しかも、その双曲線の相方は、反対側の円錐から出てきます。なぜ、こうなるのでしょうか。いったい、無限の彼方で何が起こっているのでしょうか。
また、なぜ、双曲線だけ、漸近線と呼ばれる線が必ず2本あるのでしょうか。そして、その正体はなんでしょうか。
無限の彼方で起こっている現象を考える必要が出てきました。そのためには、無限の彼方を手元に引き寄せて見える形にしなければなりません。見るといっても目で見るのではなく、頭で見るという意味ですが。
そんなこと言ったって、元々見ているのは脳なんだけど。大体、人間の目はひどい画像検出装置で、欠陥品の固まりみたいなものです。「いったい、誰がこんな設計したんだ。」、「設計不良もいいところだ。」、「これでリコールにならなのはおかしい。」などなど。ぼろくそに言われています。
しかも、その設計不良をごまかすために、脳で画像を再構成してちゃんと見えているようにしています。網膜に映ってないはずのものを勝手に付け加えたり、網膜に映っているはずのものを消したりしています。(まったく、どっかの国と同じです)
そればかりか、「第37話 光や音の話」にも書かれているように、勝手に光(伝播速度が極めて速い)と音(光とは問題にならない位遅い)とが同期しているように認識させたりしています。その他、「第78話 鏡の国の光子さん 〜鏡の不思議〜」のようなこともあるし。まあ、都合のいいように作り直してから認識させていると考えて差し支えないでしょう。
それなら、我々の脳をごまかせばいいのだから、無限の彼方を見えるようにすることも不可能ではないと考えられます。
なんか今回はインケンゼミっぽい展開になってしまった。
まずは、インケンゼミです。これは、某研究所で10年以上続いた勉強会です。概ね、毎週開催し、時々、他の場所でやったり、どっかの保養所へ行って泊りがけでやったりしていました。
そして秋葉原行軍隊を陽の組織とすれば、インケンゼミは陰の組織です。もちろん、どちらも実在する悪の組織です(本人たちが悪の組織と言ってるので)。
インケンゼミでは、対象とする内容に制限はありません。希望があればどんな内容でもやります。その点、理科好き子供の広場に相通じるものがあります。同じと言ってもいいかも知れませんね。
インケンゼミのやり方は次のようです。まず集まると、お菓子を食べながら世間話をします。それから、ちょっとだけ勉強会をして、その後、ラーメンとか、お好み焼きを食べに行きます。それで終わりではありません。更に、地下アジトと称する店へ行って、ビッグパフェを食べたりします。しかも、こいつらの一人パシリ君は、始まる前にサンドイッチを食っていたりしました。(おい、こら。食ってばっかりじゃないか)
そのため、「インケンゼミは恐ろしい組織だ。うっかり入ったら、食い過ぎで潰されてしまう。」と恐れてる人もいました。正に悪の組織です。
今度は、勉強会のやり方を説明しましょう。やりたい分野を言った奴が講師です。テキストは用いても、用いなくてもどちらでも構いません。必要に応じて、八重洲辺りにテキストの買出しに出たりします。良さそうな本をみんなで探して決めるような顔をして、パシリ君が勝手に決めてしまいます。
そして、肝心の勉強会風景ですが、テキストを決めてやると、「ここは知ってて当たり前。ここも常識。これは知らないわけないだろ。じゃ、ここからやってくれ。」と言って、いきなり5章辺りからやれされ、講師役が「すいません。1章しかやってないので、1章をやらせてください。」と言ってるのを見たことがあります。
他にも、最初に、その本の最後の章辺りのことを色々質問して、講師役が回答できないと、「なんで最後まで全部読んで理解してこないんだ。全体を理解した上で、1章はこういう位置づけにあり、これこれの理論の基礎を理解する上で必要という風に説明するもんだ。」と言っていました。
また、別なときに、「テキストや書き物見ながらやるな。全部頭に入れてこい。」と言っていました。これ、基礎となる考え方がきちんと理解できれば、それを元に精密な理論展開をするだけなので、大したことはないという考えです。教育的ですね(本当か)。
更に、感覚的な説明と、精密な説明の両方ができなければ、ちゃんと理解しているとはみなされません。感覚的に捕らえることによって、筋道の見通しを立てられるが、感覚的にやると罠にはまる恐れがあり、それを避けるために精密な説明も必要との考えです。
そうそう、忘れてはいけないのは、例を挙げるときです。「ちょっとその例を10個位挙げてくれ。」としょっちゅう言ってました。普通、どこにでも例は2、3個出ています(もし例があればの話。例が知られていない場合もある)。しかし、10個となると、調べただけでは足りませんので、自分で考え出さなければなりません。これはよい思考訓練になるとの考えです。
ちなみに、例が知られていない理論をやると、「充足可能な例がないと、その理論は砂上の楼閣に過ぎないかも知れないじゃないか。それを敢えてやるのは、何のためだ。」という突っ込みになり、回答に四苦八苦させられます。
まあ、他にも色々ありますが、省略します。3章で、パシリ君が実際にやった突込みが出てきます。
2.予備的考察
円錐曲線は、どれもよく似ています。一部を見ただけでは全く区別が付きません。

図1を見ただけで、この曲線がだ円、放物線、双曲線のどれであるか区別の付く人はいないでしょう。
まあ、よく似ているのも当然で、これら円錐曲線は2次曲線になります。もっとも、図2のように、母線を含むように切れば、交わる2直線です。母線で接するように切れば重なった直線です。
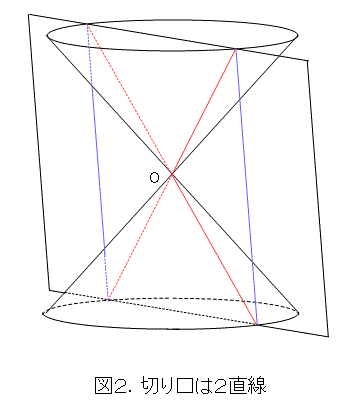
ここで、パシリ君なら、「 xy 平面みたいに、Oだけでしか交わらない平面で切った場合はどうするのか。」と突っ込んでくるでしょう(図3参照)。1点だけに見えますが、そんな回答をすると後でひどい目にあわされます。とりあえず後回しにしましょう。
さて、円錐曲線が2次曲線だということは、以下のようにして示すことができます。
まず、基本となる円錐の方程式を考えましょう。 yz 平面で、z = y という直線を考え、この直線を z 軸の周りに回転します(もちろん z = k y として考えても結構です)。
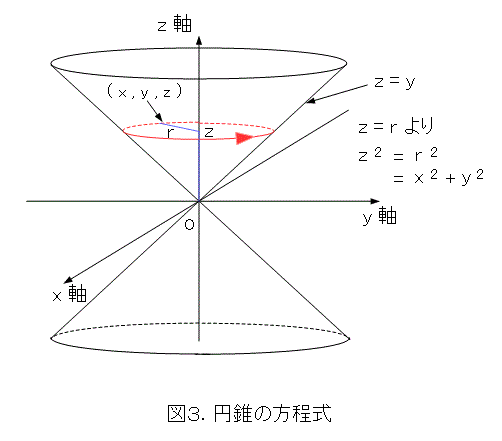
すると、図3から、円錐の方程式は以下のようになります。

ここで直線の方程式を、
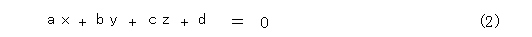
として、その交線を考えれば2次式となります。「どうしても平面上で2次式となることが見たい。」という人は、式2の定める平面上に直交座標を導入し、確かに2次式になっていることを確かめましょう。
細かいことは無視して、ともかく、円錐曲線が2次曲線になると解りました。つまり2次式で表される曲線です。
2次式だから、因数分解できるときが2本の直線で、そうでないときが本来の2次曲線になりそうですが、そうはうまく行きません。例で見ていきましょう。

式(3)は円の方程式です。これは問題ないでしょう。

式(4)は1点です。しかも原点。これは2次曲線とは言えませんね(点円ということもありますが)。これ、パシリ君の突っ込みを思い出すでしょう。

式(5)にいたっては無意味です。
これではいちいち場合分けをして考えなければなりません。なんでこうなったのでしょうか。
よく考えると、2次方程式は必ずしも実数解を持ちません。それで複素数に拡張して考えると習ったはずです。これに関して、代数学基本定理という便利な定理があります。なんと、「複素係数の多項式方程式は必ず複素数解を持つ」という定理です。
ともかく、複素数で考えると、2次方程式は必ず解を持ちます。このとき、式(4)は式(6)のように因数分解できますので、複素数の2直線っぽくなります。これで、パシリ君の突っ込みに対して回答できそうですね。

式(5)も何らかの意味を持ってくるでしょう。これを考えてみます。とりあえず、x を i x に、y を i y に変換します。そうすると、なんと、式(3)になってしまいました。つまり円です。
更に、式(3)で、y を i y に変換します。すると、

となります。これは双曲線の方程式ですね。
以上から、複素数で考えると、だ円(ここの例では円)と双曲線が同じもの(変数変換で結ばれているという意味)になってしまいました。放物線も同じようなことになりそうですが、面倒そうなので止めます。

何が面倒かというと、1次式と2次式が混ざってくるからです。扱いにくくなりそうなので、次数を揃えることを考えましょう。1次式を2次式にする最も簡単な方法は、もう1個変数を導入して、それを1次式の部分にかけてしまうことです。

返って解りにくいような気もしますが、実は、なかなか便利な表現です。元へ戻すのも簡単です。式(9)で両辺を z2 で割って、 y / z を y 、 x / z を x と置くと、式(8)に戻ります。
同様にして、式(3)で定数があるのも目障りですから、定数には z2 をかけてしまいましょう。

あれっ。どっかで見たような式が出てきました。そうです。式(1)の円錐の式です。ここでも、両辺を z2 で割って、 y / z を y 、 x / z を x と置くと、式(3)の円の式に戻ります。なんだこりゃ。そうすると、円錐を平面で切ってどうとかやってたのは、実は「一人芝居」だったわけです。
複素数を導入したり、次数を揃えたりすると、意外なつながりが見えてきます。このまま進んでもいいのですが、ここから先は実数だけで扱います(絵が描きやすいから)。自信のある人は複素数で展開してみましょう。
3.射影
この章は、実際にパシリ君がやった突っ込みの話が主です。ただし、実際は滅茶苦茶強烈であるため、理科好き子供広場用に修正しています。(以下の「う」だけ美化200%です)
まず、本稿の趣旨に則り(のっとり)無限の彼方を手前に持ってくることを考えます。 美術で、透視法(一点透視法や二点透視法)を習ったことがあると思います。これは、平行線が1点で交わっているように描く技法です。絵を描くときに、1点から出た光線上に、物体のふちが乗っているように描かないで怒られたことのある人もいるでしょう(俺だけかも)。わざわざ定規を当てて、1点で交わっておらず滅茶苦茶だとか言われた経験はありませんか(やっぱり俺だけかも)。
この現象を利用しましょう。実際に、無限の彼方の点を手前に持ってこられるのですから。それと、光線に乗っている部分の追跡といえば、光によって影がどうなるかですね。これをうまく概念化したものが射影です。
ちなみに、秋葉原行軍隊は光で、インケンゼミは影です。何しろ、秋葉原行軍隊の行動は昼間、陽の光の中ですし、インケンゼミの行動は主に夜、地球の影の中です。最初の方で書いた陽と陰の理由はこんなところにあったんですね。
ともかく、話を進めましょう。折角なのでインケンゼミに登場してもらいましょう。参加者はパシリ君と「あ」、「い」、「う」の4人です。今回の講師は「う」です。
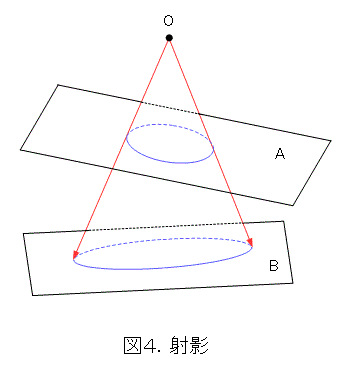
「う」は図4のように、点Oから出た光によって、平面Aの上にある図形が、平面Bの上に写されるのが射影だと説明しました。普通によくある射影の説明ですね。
しかし、こんな説明では、ちゃんと理解していないなと思われてしまいます。案の定、パシリ君から以下のような突込みが入りました。
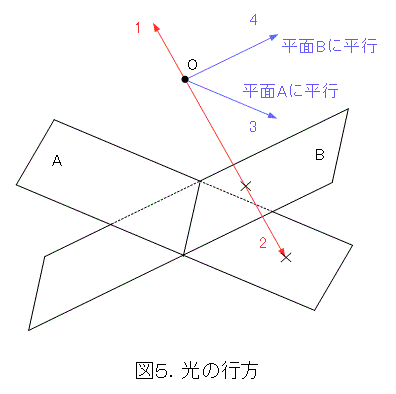
「Oから出た光1はどこへ行くのか。」、「Oから出た光2では、平面Aより先に平面Bを通過してしまう。どうやって平面Aの図形の像を平面Bの図形に写す気だ。」、「平面Aに平行な光3はどこへ行くのか。」、「平面Bに平行な光4はどこへ行くのか。」
これが答えられれば、円錐曲線三兄弟の正体まで辿り着けます。「う」の方では、光1、2は寝耳に水の突っ込みです。光3、4は一応用意してきた説明でなんとかなりそうです。今までさんざんな目にあった経験から、説明の順序に意味がありそうだと「う」は感じ取りました。うっかり、光3、4を先に説明すると、何か見落としがあって、更にそれを突っ込まれ、ひどい目にあわされそうです。
ここは、順序に従って説明した方がよさそうです。一方、「あ」と「い」はお菓子を食って眺めています。
「う」は、「僕が回答するんですよね。」とか、「光が無限の彼方へ飛んでいくんですよね。」などと言ってましたが、その類(たぐい)のことは全部省略します(だから「う」だけ美化200%)。
図5をよく見ると、光1、2は同一直線上に乗っています。だいたい、パシリ君は突っ込みの中にヒントを置いておくことがよくあり、さすがにこの部分は「う」も見抜いています。それでは回答を考えて行きましょう(俺が「う」の立場で回答を考えて書くというのはおかしいが、まっ、いいか)。
まず第1に、余計な制約は考えないということが重要です。今回、光が有限の速さだなどと考える必要はありません(そうしないと無限遠に到達できなくなる)。また、同じものでも、扱っている事象によって、全くの別物として考えることはよくあります。
光1は無限の彼方に消え去っているように思えますが、そうではなく、反対の方から戻って来ると考えてみましょう。つまり、光2の線上を逆向きにOへ戻って来るということです。そうすれば、平面Aの像が平面Bに出来て問題ありません。逆に、光2は無限の彼方へ飛んで行き、光1の線上を逆向きにOへ戻って来ます。
つまり往路と復路を考えるわけです。光線逆行の原理と照らしても妥当だと思われます。この場合、光1でも光2でも、それぞれ平面Aと平面Bを1回だけ横切ります。これをパシリ君に説明すると、「で。」と言われました。
まだ何か説明が不十分なのでしょうか。よく考えましょう。光1と光2は同じ線上をOから出て、Oへ戻って来ており、向きの違いしかない。しかし、光は無限に速いと考えているので、平面Aと平面Bに対しては同じ作用をする。追加説明すると、無限に速いので、平面Aと平面Bは同時に通過するということです。そうすると、光1と光2が乗ってる直線の性質だけが問題となってきますね。
以上から、光は直線として考えるのが妥当と思われます。こうして、「う」は光1と光2とを統合して、光を直線として扱うと回答しました。これで、最初の二つの突っ込みの回答が得られました。
幾何光学では、光を直線(光線)として扱うところから始まります。これ、ユークリッド空間を前提としています。空間に歪みがあったり、媒質が均一でなかったりした場合は測地線になります。そういえば、最近は、幾何光学の書籍を全然見かけません。どうなってしまたのでしょうか。
さて、光を直線と考えてしまえば、平面Aの像を平面Bとしても、平面Bの像を平面Aとしても、どちらでも同じになります。したがって、後の二つの突っ込みはどっちでも同じと考えてよくなりました。危ないところでしたね。後の二つの突っ込みの回答を先にやっていたら、「何が違うのか。その違いはどこから来るのか。」と突っ込まれていたことでしょう。
更に、普通にあるように、無限遠点を付け加え、「無限遠点の集まりが無限遠直線だ。」などとやろうものなら、「なんで、無限遠点の集まりが直線になるんだ。ちゃんと根拠を示して説明しろ。」と間違いなく突っ込まれます。
後の二つの突っ込みの回答に先立って、射影によって直線が直線に写るということを示しておきます。ただ、例外があるのですが、とりあえずは無視しておきます。
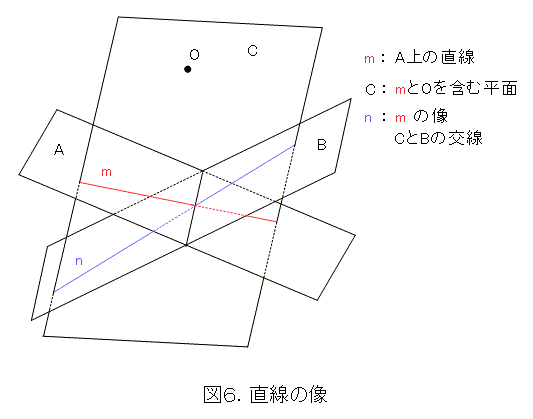
図6にあるように、平面と平面の交線は直線ですから、直線の射影による像は直線です。平面Bと平面Cが平行になる場合は、とりあえず無視しておきます。
後の二つの突込みを考えるときが来ました。
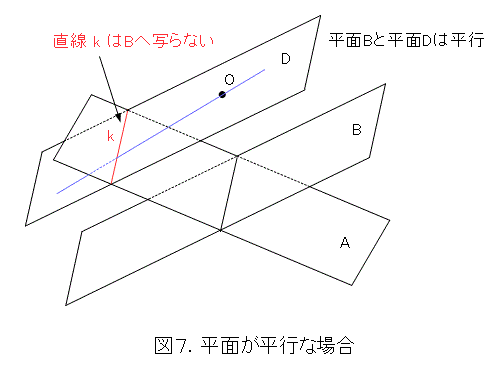
どっちでも同じなので、平面Bに平行な光を考えます。Oを出て平面Bに平行な光は、図7の平面Dに乗っています。当然ですが、平面Bと交わりません。平面Dと平面Aの交線を k とすれば、直線 k の射影が平面Bへ写ることはあり得ません。
同様なことが平面Bでも言えますので、平面B上に、平面Aに対応しない直線があります。すると、平面Aと平面Bとは完全に対応してはいないことが解ります。これが、今まで、「射影」と言ってきて、「射影変換」と言ってこなかった理由です。
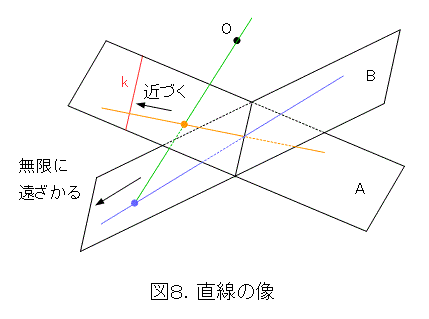
直線 k の取り扱いを考えましょう。図8のように、平面Aの直線上を k に近づくと、平面Bの対応する直線上では無限の彼方へ飛んで行きます。これから、直線 k の射影に該当する直線を、仮想的に、平面Bに付け加えるのがよさそうです。
これを無限の彼方にある直線(正確に言うと、直線の射影に対応している)という意味で「無限遠直線」と呼びます。そして、図8のように、平面Aで直線 k と直線上の交点に対応する点を「無限遠点」と呼びます。この無限遠点は、平面Bに射影された直線と無限遠直線との交点と考えて差し支えないでしょう。つまり、平面Bの直線に無限遠点が付け加えられていると考えられます。
こうして「う」は3番目と4番目の突っ込みに回答しました。ところが、パシリ君は、「なんか見落としてないか。」と言いました。「う」はあせって考え直し、「いや、気が付くかどうか試したんですよ。」と苦し紛れの言い訳をしています。
これを見ていて、「あ」は、「「う」は、また顔色見てそんな言い訳ばかりしてる。」、「い」は、「糖分の取り過ぎだ。」と言ってました。
まあ、ともかく、「う」の説明で何が悪かったんでしょうか。平面B上の直線は、直線に無限遠点という1点を付け加えています。上で付け加えた無限遠直線はこの1点が付け加えられていません。この点がないと、直線 k と平行な直線を考えたときに破綻します。
どうしてか考えましょう。平面Aで直線 k に平行な直線を考えます。すると、この直線は直線 k と交わらないため、その射影となる平面Bの直線には無限遠点が付け加えられません。これでは、無限遠点を持っているものと、持っていないものが混在することになり、平面の均一性がありません。都合が悪いので、あえて、無限遠点を付け加え、直線 k 上を無限の彼方へ行った先の点の射影と考えます。(直線 k 上の点の射影と、今付け加えた点の射影のみが無限遠点となることに注意しましょう)
この無限遠直線に、更に1点を付け加えたものが、本当の無限遠直線です。しかも、ここでの考察から、直線 k に平行な直線の射影は、全ていま付け加えた無限遠点を持っていなければなりません(1点の射影なので1点ですし、これ以外に対応する点はありません)。つまり、平面Aで考えると、直線 k に平行な直線は全て、直線 k に付け加えた点で交わっていることになります。
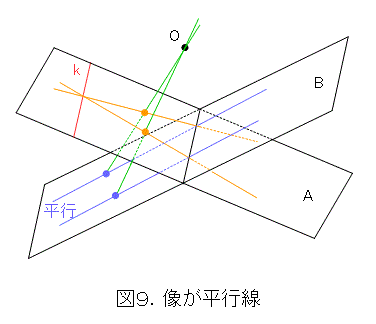
再び、平面Aの直線 k と交わる直線に戻ってみると、直線 k の同じ点で交わる直線群は、射影が平行線になります。つまり、これらの平行線は同じ無限遠点で交わっていると考えられます。
散々な目にあいましたが、ようやく、パシリ君の突っ込みに回答できました。どう考えても、「う」が美化されすぎてるな。実態はこんなにすんなり回答できていません。
ともかくここまでくれば、円錐曲線三兄弟の正体が解ります。(4章以降でちゃんとやるので、ここは感覚的な説明とします。どうしてもという人は、円錐をうまく描いて、本当にうまくいってることを確かめましょう)
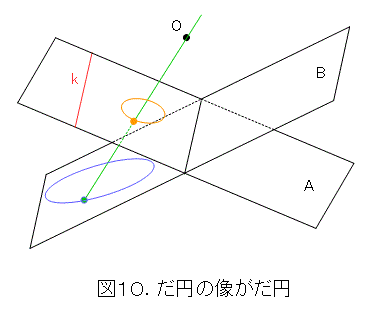
図10のように無限遠直線から離れている場合はだ円であることが解ります。
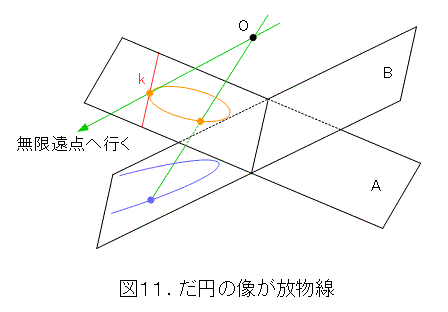
図11のように、無限遠直線と接している場合は放物線となります。
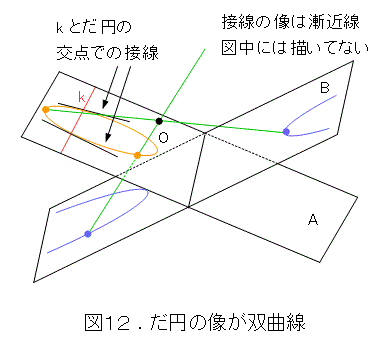
図12のように、無限遠直線と交わっている場合は双曲線です。しかも、交点での接線が漸近線となります。自分で漸近線まで描いた図を描きましょう。
簡単に書くと、図13のようになっています。
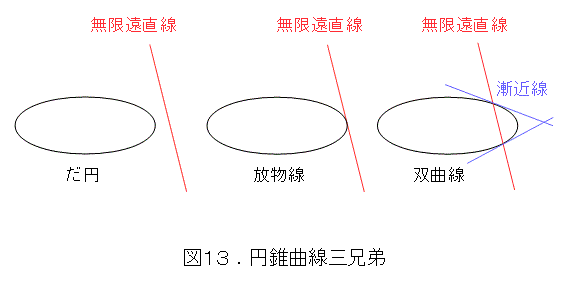
図13を見れば明らかですが、放物線の場合、ちょっとでも動かすと、無限遠直線と離れたり、交わったりします。これが、第6話図22の放物線が一瞬しか現れない理由です。
4.射影平面と射影変換
感覚的に、円錐曲線三兄弟の正体が解りましたので、それを精密に(実は手抜き)示します。
まずは射影直線から考えましょう。前章で扱った、直線に無限遠点を付け加えた直線が射影直線です。
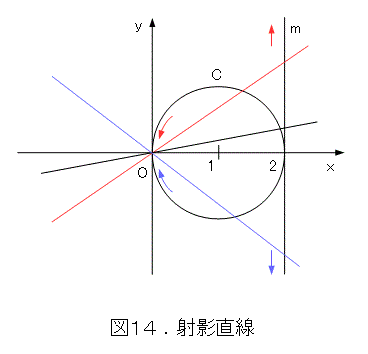
xy 平面で、( 1 , 0 ) を中心に半径1の円Cを考え、( 2 , 0 ) を通り、y 軸に平行な直線 m を引きます。この上で、原点を通る直線を考えましょう。この直線によって、円Cの点と直線 m の点は、原点を除いて1対1に対応します。こういうとき、「う」は「あ」に、「じゃ、直線の方程式を決めて、円Cとの交点と直線 m との交点を求めてくれ。」と言います。しかも、「いい質問ですよね。」とパシリ君の顔色を伺います(パシリ君はこんな計算どうでもいいと思っていますが)。ここでは交点座標を省略しますので、自分で求めてみましょう。
図14から、直線 m 上を上に行っても、下に行っても、円Cの対応点は、結局、原点に近づきます。これから、原点が無限遠点に対応していると考えるが妥当でしよう。つまり、直線に無限遠点を付け加えた射影直線は、円みたいな感じのものになるということです。実際には、直線は曲がっていませんので、語弊がある言い方ですが。
図14をよく見てみましょう。点と点の対応を行っているのは原点を通る直線です。y 軸を除いて、原点を通る直線が決まれば、それぞれ、円Cと直線 m の点が決まり、逆に、原点を除いて、円Cの点または直線 m の点が決まれば、原点を通る直線が決まります。
更に、原点は直線 m の無限遠点に対応し、y 軸は直線 m に平行です。前章で、平行線は無限遠点で交わるとしましたから、y 軸は無限遠点に対応していると考えて差し支えないでしょう。
こう考えてくると、原点を通る直線を点とみなしたその集合が射影直線と考えられます。初めての人には考えにくいと思いますが、訓練して慣れましょう。確実に世界が広がります。
人間は(だけではないかも知れない)、目に映ったものよりも、脳で認識したものが見えています。たとえば、「なんとか大学は優秀だ。」と言った場合、個々の学生や教授などに目を向けているのではなく、大学という入れ物に対するイメージで判断しています(しかも、有名大学というだけで、勝手に優秀だと判断していたりします)。
元へ戻って、原点を通る直線は、傾きだけで決まります。そして、傾きは、x 座標の増分と、y 座標の増分の比です。この比を ( x : y ) と書くことにしましょう。どちらかが0になることは許しますが、両方とも0になることは除外します。そもそも、両方とも0のときは原点そのものになってしまい、直線ですらありません。
ここで、x が0でなければ、y / x は原点を通る直線の傾きそのものですし、 x が0のときは、( 0 : 1 ) は y 軸です(比が問題なので、代表的な数値で書いた方が解りやすくなります)。ちなみに、( 1 : 0 ) は x 軸です。
原点を通る直線を点とみなし、その集合が射影直線でしたから、射影直線上の点は、( x : y ) となります。
さあ、ここまでの準備をして、射影平面を考えましょう。今度の場合、球を描くことに意味はありません。射影直線では、直線に1点を付け加えてましたから、丁度、円とうまい対応関係ができました。しかし、射影平面では、平面に無限遠直線を付け加えるため、1点を付け加えて球面ということにはなりません。どうしても射影平面を無理やり描いた曲面の絵が見たい人は、「射影平面」で検索して探しましょう。多分、誰かが描いているはずです。
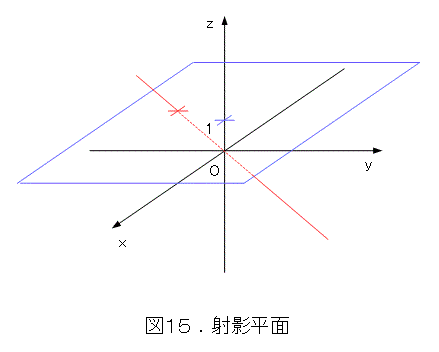
まず、xyz 空間で、z = 1 という平面を描きます。次に、原点を通る直線とこの平面の交点を考えます。原点を通る直線が、xy 平面に乗ってない限り、平面と直線の交点は1個定まります。また、xy 平面上の直線は z = 1 という平面に平行です。
これから、原点を通る直線を点とみなして、射影平面を定義するのが妥当だと解ります(射影平面をP 2 (R) と書きます。複素数を基にした場合は、P 2 (C)) 。そして、xy 平面上の原点を通る直線群が無限遠直線となります。ついでに書いておきますが、xy 平面上の原点を通る直線群は、直線に無限遠点を付け加えたものになっています。パシリ君の最後の突っ込みの正体はこれだったんですね。
射影直線のときと同じように考えて、原点を通る直線は、x 座標の増分と、y 座標の増分と、z 座標の増分の比で決まります。したがって、この比を ( x : y : z ) と書くことにしましょう。同時に2個まで0になることは許しますが、全部同時に0になることは除外します。そもそも、全部0のときは原点そのものになってしまい、直線ですらありません。もちろん、射影平面P 2 (R) を ( x : y : z ) ( x、y、z が同時に全部0になることは除く)の集合と定義しても同じです。
ちなみに、xy 平面は、無限遠点の集まりですので、無限遠直線になり、このときは ( x : y : 0 ) です。また、 ( x : y : 1 ) は通常の平面(ユークリッド平面という)となります( z が0でなければ何でも同じ。比だけが問題なのだから、 ( x : y : z ) の各成分を z で割ればよい)。図15で、通常の平面がちょっと浮いているため(青い平面)、変な感じがするかも知れませんが。
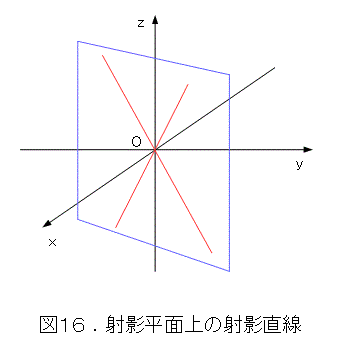
射影平面上で、射影直線を考えましょう。どう考えればいいのでしょうか。射影平面上の各点は、xyz 空間上の原点を通る直線でしたから、異なる2点を描くと図16の赤い線のようになります。すると、この2直線を含む平面がただ一つ存在します(しかも原点を通ります)。これを射影直線としたらどうでしょう。
よく知られているように、通常の幾何学(ユークリッド幾何のこと)では、異なる2点を通る直線はただ一つ存在するというのがありましたね。丁度、それと同じです。しかも、既にやったように、xy 平面(方程式は z = 0 )は無限遠直線であり、原点を通る平面が射影直線の実例となっています。
ということで、原点を通る平面を射影直線とすることは妥当と考えられます。式で書くと、式(11)のようになります。

式(11)をよくながめると、 x 、y 、z の比だけが問題になる方程式です。つまり、 ( x : y : z ) が乗っている点となり、うまくいっています。
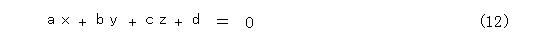
式(12)のような方程式はだめです。 x 、y 、z の比だけが問題になる方程式ではありません。( x , y , z ) そのものが問題となってしまいます。つまり、( x : y : z ) が乗っていません。
このようにして、射影平面では、同次式(全項の次数が全て同じ式)だけが問題となります。我々は、2次式を考えていますので、以下の式(13)だけが対象となります。
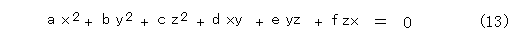
式(13)で z が0でないときは、両辺を z 2 で割り、x / z 、y / z を改めてx 、y と置きなおせば式(14)のように普通の2次方程式(したがって、普通の2次曲線)となります。項の順番が悪いため、多少見にくいとは思いますが。
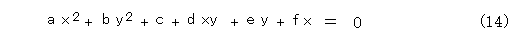
次に、射影変換を考えましょう。
まず、変換というのは、1対1に対応している写像(全単射)のことです。また、射影というのは、直線を直線に写す写像のことです(図6参照)。したがって、射影変換は、直線を直線に写す1対1の写像のこととなります。
このことから、式(15)のような1次変換みたいなものを導けますが、詳細は省略します。自分で考えるか、射影幾何の本を読んで勉強されることを薦めます。
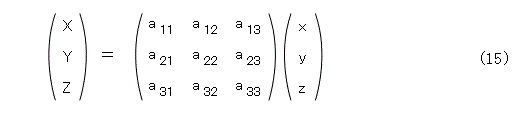
ただし、式(15)の右辺の係数行列(変換行列)は逆行列が存在するものに限ります(行列式が0にはならない)。
このとき、 x 、y 、z の比 ( x : y : z ) によって、 X 、Y 、Z の比 ( X : Y : Z ) が決まり、 ( X : Y : Z ) は射影平面P 2 (R) に含まれます。自分で式を書き下して確かめましょう。
また、( x : y : z ) が直線に乗っていれば、( X : Y : Z ) も直線に乗っています(当然ですけど)。これを確かめるには、( x : y : z ) が乗ってる直線を式(11)として、式(15)を逆に解いた式(16)を式(11)へ代入して確かめます。面倒がらずに自分でやりましょう。
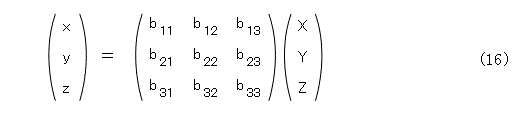
さて、ここまでの準備ができると、射影変換でだ円、放物線、双曲線が写りあっていることが示せます(前章の図10、11、12に対応します)。


出発点とするだ円ですが、式(17)では係数が付いて回って解りにくいので、式(18)とします。式(17)を出発点とする計算は自分でやってみましょう。(他人には面倒がらずにやれと言って、自分では面倒なことをやらないなんて、ひどい話ですね)
式(18)を射影平面に持ってくるために、x 、y をそれぞれ x / z 、y / z で置き換えて分母を払い、式(19)とします。

左辺に項を集めて式(20)とします。

式(20)を射影変換して、双曲線や放物線にすることを考えましょう。まず、曲線の変換は、図17のように、逆変換し曲線の方程式へ代入して求めます。
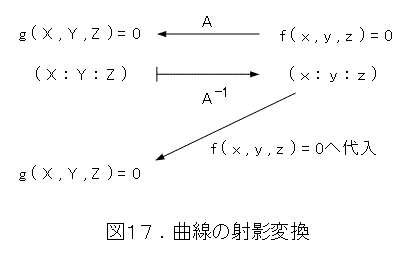
いちいち逆変換すると、式がごちゃごゃして見にくくなるので、式(16)をもとにして逆変換側の方から扱います。
一般的には、求めたい式を書いて、それと射影変換結果を比較して変換行列を求めますが、ここでは、視察によって求めます(手抜きともいうが、感覚を高める訓練にもなっています)。
最初に、双曲線への射影変換を考えます。式(20)を眺めると、y と z を入れ替えれば双曲線ができそうです。
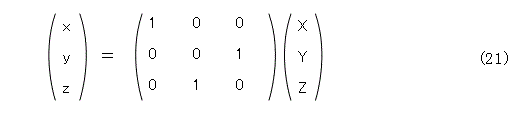
式(21)の変換結果を、式(20)へ代入して次の式を得ます。

変形して、

ここで、X / Z 、Y / Z をそれぞれ x 、y とおけば、

となります。これは双曲線の方程式です。
次に、放物線への射影変換を考えます。再び、式(20)を眺めます。今度は、y を y + z 、z を y - z と置き換えれば2乗の項が消えてよさそうです。
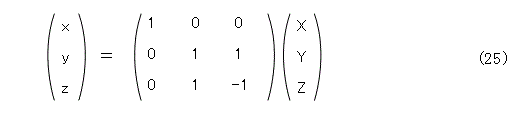
式(25)の変換結果を、式(20)へ代入して次の式を得ます。
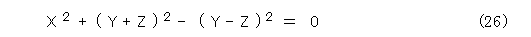
変形して、

ここで、X / Z 、Y / Z をそれぞれ x 、y とおけば、

まさしく放物線の方程式になりました。これが、「第6話 鏡の国の光子さん その二」の終わりの方に書いてある「三面怪人」の理由です。
5.接線
ここまでで、射影幾何の立場では、だ円、放物線、双曲線の区別がなくなりました。残る問題は、図13にある、無限遠直線との位置関係で違うように見えるという部分です。そのためには、接線についての考察が必要です。
接線といっても、2次曲線が対象なので、ゴリゴリ計算してやっていくことは可能です。しかし、式がやたらと長くなり、見づらくなるので、もっと簡単に書ける方法を採ります。
最初に、接線のおさらいです。接線の方程式は、陽関数なら簡単なのに、陰関数になると、とたんに面倒になります。こんなところにもインケンゼミの「陰」が出てくるのですね。それはともかく、陰関数の接線の方程式を書き表すことを考えましょう。
準備として必要なのは「偏微分」です。変数は何個(2個以上)でも同じなので、3変数の多項式 f ( x , y , z ) を考えます。
多項式 f ( x , y , z ) を x で偏微分するというのは、x だけを変数とし、y , z を定数として微分することです。このとき偏導関数は式(29)のように書きます(三種類書いています)。
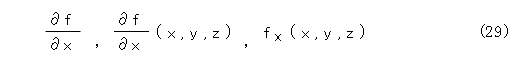
点 ( a , b , c ) での x に関する偏微分係数は式(30)のように書きます(二種類書いています)。
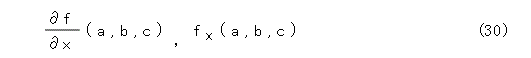
y , z に関する偏微分も同様です。なお、偏微分については、微積分の本に必ず出ているので、そちらを参考しましょう。
次に、接線の方程式です。まずは、xy 平面で、g ( x , y ) を2変数の多項式として、曲線 g ( x , y ) = 0 (陰関数表示)を考えます。このとき、曲線上の点 ( a , b ) における接線の方程式は式(31)のようになります。
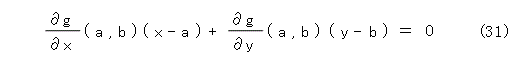
陰関数の接線についても微積分の本に必ず出ているので、そちらを参考しましょう。
さて、射影平面P 2 (R) で考えましょう。前にも書いたように、多項式 f ( x , y , z ) は同次式とします。つまり、x 、y 、z について、どの項も次数が同じです。式(13)の左辺を思い浮かべましょう。
このときに、曲線 f ( x , y , z ) = 0 上の点 ( a : b : c ) での接線の方程式は、式(32)のようになります。そもそも、射影平面上の射影直線は、xyz 空間上の原点を通る平面でしたから、式(31)より、やや簡単な式になります(変数は増えてますが)。
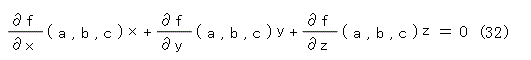
6.円錐曲線三兄弟の正体
いよいよ最終段階です。だ円、放物線、双曲線と無限遠直線の関係を調べましょう。なお、係数を一般化しても複雑になるだけなので、簡単な場合について調べます。気になる方は、一般的な場合で調べましょう。
まずは、だ円から調べます。

式(33)はこれまで何度も出てきました。xy 座標で考えれば単位円になっています。無限遠直線の方程式は、z = 0 でしたから、これを式(33)へ代入すると、

となります。射影平面P 2 (R) では x 、y 、z 全部が同時に0になることは許されませんから、式(34)の解はありません。つまり、だ円は、無限遠直線と離れているということです。これで、図13の左側の絵が確かめられました。
次は、放物線です。

式(35)は放物線の式です。xy 座標で考えれば、y = x 2 です。とりあえず、点 ( a : b : c ) での接線の方程式を求めましょう。

無限遠直線との共有点を求めます。無限遠直線上では、z = 0 でしたから、式(35)より、x = 0 となり、無限遠直線と放物線の共有点は ( 0 : b : 0 ) (ただし、b は0でない)です。比だけが問題でしたから、 ( 0 : 1 : 0 ) が共有点となります。式(36)へ代入すれば、z = 0 となって、確かに無限遠直線が接線になります。これで、図13の中央の絵が確かめられました。
最後は、双曲線です。

式(37)は双曲線の式です。xy 座標で考えれば、x 2 - y 2 = 1 です。今度の場合、式(37)と無限遠直線の交点を求め(2個あるはず)、次にこの交点での接線が漸近線になっていることを確かめます。
式(37)で z = 0 とおくと、式(38)のように因数分解されます。

これから、x - y = 0 、x + y = 0 が出て来ます。これらはそれぞれ、( 1 : 1 : 0 ) 、( 1 : -1 : 0 ) という点です(あくまでも比だけが問題です)。確かに、双曲線と無限遠直線の交点は2個あることが解りました。
あとは、この2点での接線が漸近線になっていることを確かめれば完了です。接線の方程式を求めましょう。


なんだこれ、式(38)と同じじゃないかと思われるかも知れませんが、式(38)では、z = 0 がくっついています。そのため、点となりますが、式(39)、式(40)では、zは任意なので、直線の方程式になっています。この点に気をつけましょう。
xy 座標で式(39)、式(40)考えれば、x - y = 0 、x + y = 0 という直線になります。これは、x 2 - y 2 = 1 の漸近線になっています。こうして、図13の右側の絵も確かめられました。
結論として、円錐曲線が三兄弟なんて真っ赤な嘘です。同じ曲線が、無限遠直線との位置関係で違って見えているにすぎません。こういう人、よくいますよね。相手によって、全然態度の違う人が。
5.おわりに
今回、接線のところで手を抜きすぎたような気がします。微積分について、どこかで扱っておき、参照する形にしておいた方がいいのかも知れませんが、とりあえず止めておきます。
それはそうと、見えないものに対して、なんとか見ようとする努力は日々続けられています。望遠鏡や顕微鏡、X線透視装置など、枚挙に暇(いとま)がありません。そして、ここでは無限という見えないと思われていたものに対し、見るという試みの一つを行いました。当然ですが、無限についても、色々な意味の無限があり、それぞれに取り扱いが工夫されています。
勉強方法にしても、これが絶対というものはありません。本稿で示したような、最初に当たりを付け、イメージを描き、理論的に展開するというやり方はその一つでしょう。それがいいかどうかは、やってみた本人が考える問題です。本稿を読まれた方はどうお考えでしょうか。
完
平成27年6月27日
著作者 坂田 明治(あきはる)
|