|
第92話
初等幾何におけるパラドックスの話
|

「読者への期待」
本稿の狙いは、誤った出発点や、誤った推論から誤った結論を導くことです。このような過ちに陥らないように、実際に作図を行い、自分で考えることの重要性を知る必要があります。世の中には、人をだまそうとする輩がおり、それに引っ掛からないための思考訓練と思っていただければ幸いです。
本 文 目 次
1.はじめに
4.円の中心は二つ
5.64=65
6.おわりに
著者 坂田 明治
第92話 初等幾何におけるパラドックスの話
1.はじめに
「第91話 立方体の倍積の作図」において、自分で正確な作図をしないと、とんでもない結論が出てしまうということを見ました。「全ての三角形は二等辺三角形」というのがそれです。ネットで検索し、適当に斜め読みをして、鵜呑みにするということは危険です。必ず自分でよく考えましょう。これは全てについて言えることです。
今回は、初等幾何の有名な例をいくつか出して、誤った結論に導かれることを楽しみましょう。種明かしはしませんので、自分で正しい図を正確に描いて考え、誤りを見抜きましょう。なお、本稿の図形は全て定規とコンパスで作図できます。
2.直角は鈍角に等しい
まず、長方形ABCDを用意しましょう。長方形なので、どの角も直角、向かい合う辺は平行で長さが等しいということを頭に入れておきましょう。
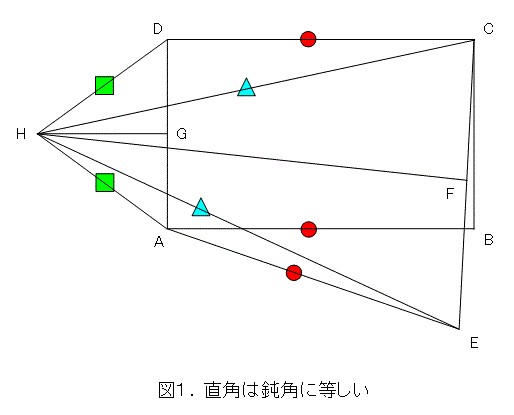
AB = AE となるように、長方形ABCDの外側に点Eを取り、線分AEを引きます。
次に、それぞれ、ECとADの垂直二等分線を引き、その交点をHとします。そうすると、



なので、

が成り立ちます。
合同ですから対応する角は等しいので、

となります。
また、垂直二等分線の性質から、

ですね。
(5) − (6)を求めて、

です。
ところで、


ですから、直角は鈍角に等しくなります。
3.1点から1直線へ2本の垂線が引ける
まず、円P、円Qが2点A、Bで交わっているとしましょう。予備知識として、円の直径を1辺とし、円に内接する三角形は直角三角形(直径に相対する角が直角)であることを頭に入れておきましょう。
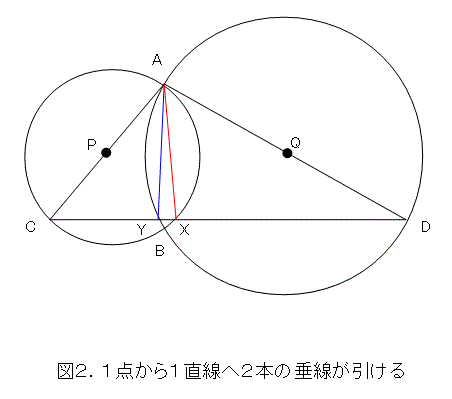
円PのAを通る直径をC、 円QのAを通る直径をDとします。そして、C、Dを結ぶ直線が円P、円Qと交わる点を、それぞれX、Yとしましょう。
三角形AXCは直径ACを1辺とする三角形だから、

が成り立ちます。
同様に、

となります。
式(10)(11)をよく見ると、点Aから、直線CDへ2本の垂線が引けました。
4.円の中心は二つ
まず、角XOYを用意しましょう。今度は、円に内接する直角三角形の、斜辺上に円の中心があることを頭に入れておきましょう。
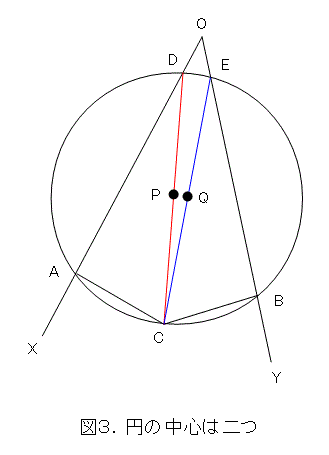
OX上に1点Aを取り、OY上に1点Bを取ります。そして、点Aから、OXに垂線を立て、同様に、点BからOYに垂線を立てます。この交点をCとします。
3点、A、C、Bを通る円を描き、円と、OX、OYの交点を、それぞれD、Eとします。
こうすると、三角形ACDは円に内接する直角三角形ですので、斜辺CD上に円の中心Pがあります。同様に、斜辺CE上に円の中心Qがあります。
したがって、円には中心が二つあることになります。
5.64 = 65
今度は、図形を切り貼りしても、面積は変わらないということを頭に入れておきましょう。なお、方眼紙上に作図した方が楽です。更に、カッターと厚紙と縁の厚い定規を用意して実際に切り貼りしてみましょう。
まず、一辺の長さが8の正方形ABCDを用意します。
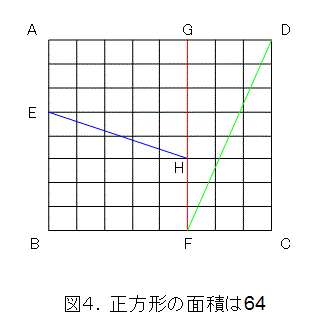
面積を計算しましょう。
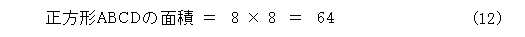
また、図4にあるように、点E、F、G、Hを取り、EH、FG、FDによって四つに分割します。
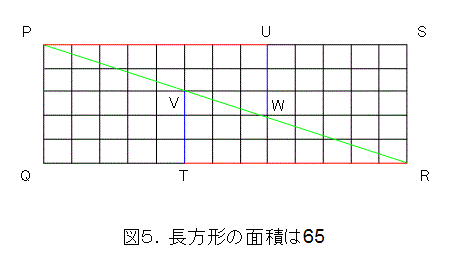
次に、辺の長さが5と13の長方形PQRSを用意します。
面積を計算しましょう。
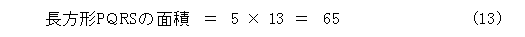
これも、図5にあるように、点T、U、V、Wを取り、PR、VT、WUによって四つに分割します。
このときに、直角三角形、二角が直角の台形をそれぞれ見比べて、



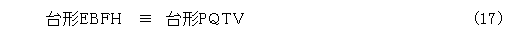
となることが解ります。
したがって、

となり、

が成り立ちます。
6.おわりに
今回は、実際に作図をし、論理的に考えれば誤りに気づくものです。この意味で簡単な問題といえるでしょう。しかし、現実社会では、論理で考えて済むものばかりではありません。実に難しい面もあります。
何度も書きましたが、何事も疑ってかかり、正しい状況でちゃんと考える必要があります。なんとか詐欺にしても、誤った状況を作り、そこに落とし込むことによって、誤った判断に持ち込んでいます。常に冷静にというのも難しい問題です。どっかの宇宙人みたいに感情が無く、理性によって行動しているというなら別でしょうが。(それ、何度も見たけど、理性的とは思えない行動ばかりとっていますね)
どっかの国では、国民に真実を隠し、都合のよいデータを基にして、都合のいいように話を進めたりしています。景気が回復しているとか言ってるけど、景気のよいところばかり取り上げ、都合の悪いところを隠しているとしか思えません。売り上げが落ちたり、収入が減った上に、税金が増えてぼやいている人はほとんど取り上げられませんね。
とにかく、自分で実際にやってみて考えることが第一歩です。
完
平成26年6月20日
著作者 坂田 明治(あきはる)
|