|
第93話
数に関するパラドックスの話
〜数値をどこまで信用できるか〜
|

「読者への期待」
本稿の狙いは、数値にだまされやすいということを認識することにあります。これは、誤った出発点や、誤った推論からの誤った結論に起因します。このような過ちに陥らないように、出発点となる仮定を見抜き、正しい推論過程を経ることの重要性を知る必要があります。そのための思考訓練と思っていただければ幸いです。
本 文 目 次
1.はじめに
3.消えた100円
5.数値は何でも同じ
6.おわりに
著者 坂田 明治
第93話 数に関するパラドックスの話
〜数値をどこまで信用できるか〜
1.はじめに
今回は数に関するパラドックスを扱います。前回と比べ、断然、人をだましやすいのはこっちの方です。数値が出てくると、他人どころか、自分までもだまされたりします。何度も書いていますが、常に疑ってかかり、自分で考えことが大切です。
解説はちょっとしか付けません。自分で調べてよく考えましょう。
2.過去の人口の方が多い
過去の人口はどうだったかを考えましょう。人間は単為生殖ではありませんから、必ず、父親と母親がいます。当然、その父と母も、一代前の父と母から生まれました。更に、その一代前の父と母も、二代前の父と母から生まれました。
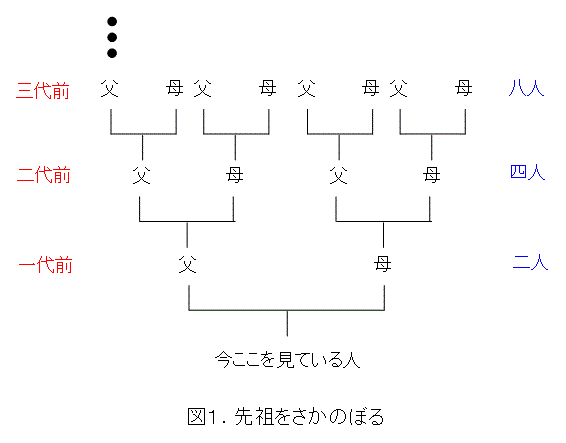
こう考えると、一代さかのぼるごとに、人口は2倍に増えます。十代さかのぼると1024倍になり、二十代さかのぼると、1048576倍になります。約100万倍です。
ちなみに、コンピューターに関わっている人は「2べきの呪い」から抜け出せませんので、2の10乗を1000、2の20乗を100万と即答します。
それはともかく、過去の方が人口が多くなっていますね。
この問題は、「記念館二階 暮らしと微生物 曖昧模糊(あいまいもこ)」の「170.空気や先祖を共有する地球家族」に出ています。下記ページのメニューから入ってください。
そして、これこそが「理科好き子供の広場」にとって特に重要な意味を持っています。著者と田口先生とのお付き合いの始まりだからです。もし、この話がなければ、「理科好き子供の広場」が立ち上がったかどうか分かりません。仮に立ち上がっても現在のような内容にはならなかったでしょう。
3.消えた100円
ここでは「秋葉原行軍隊」の内3人が登場します。 秋葉原行軍隊というのは、1990年頃から秋葉原に出回っている連中です。
こいつら、新田次郎著「八甲田山死の彷徨」(彷徨はほうこうと読む)を読んではまり、自分たちを秋葉原行軍隊と呼んでいます。雪が降ってるときや、台風が接近しているときも秋葉原行軍をやっています。雪が降っているときは「雪中行軍だ。」と喜んでいたし、台風が接近しているときは、「そんなことで止めたら軍隊といえるか。」とか言っていました。
なお、あくまでも新田次郎の小説の方にはまったのであって、八甲田山で実際にあった事故の方ではありません。そういえば、この小説を実話と思い込み、研修で使っている人もいるようです。実際には、31聯隊(れんたい)が無事で、5聯隊が全滅しかけたのは「運」だけです。小説の方はあくまでも小説であって、色々と脚色し、指揮の問題にしています。
横道にそれましたが、ここで出てくる秋葉原行軍隊は、損氏少佐、くぐつ大尉、悪童子大尉の3人です。以下、この3人は実際の人物であって、脚色はちょっとだけです。
大体、行動パターンはいつも同じで、損氏少佐がくぐつ大尉に秋葉原行軍計画を立てさせ、くぐつ大尉を「教導」だとしておいて、途中から「斥候」に出させたりします。
以前は、秋葉原内で行ったり来たりしてましたが(彷徨という)、秋葉原の変貌(へんぼう)とともに、段々行く店がなくなりました。現在は、秋葉原からアメ横へ行き、戻ってきて神田の飲み屋に行っています(全行程徒歩)。ちょっと行動を覗いて(のぞいて)みましょう。
まず、くぐつ大尉に秋葉原行軍計画を立てさせ、集合地点に集合後、昼食をとりに行きます。くぐつ大尉が調べて、候補の店を挙げると、いきなり、損氏少佐は、「今日はカレーが食いたい。」と言って、くぐつ大尉の探してきた店を無視してカレー屋へ行きます。
他にも、神田で実際にあった話。
悪童子大尉「このコーヒー屋は見覚えあるであります。」
損氏少佐「本当か。くぐつ大尉、飲み屋への道はこっちでいいのか。」
くぐつ大尉「我々にはインターネットがある。間違いない。」
と会話が続いて、目的の飲み屋にたどり着けませんでした。
まったく、こいつら。
これ、コーヒー屋は飲み屋から駅に行く途中で寄ったのだから、駅へ行く途中でコーヒー屋の見える位置を通ったと推理して、やっと目的の飲み屋へたどり着けました。損氏少佐と悪童子大尉が笑い転げ、後々まで話のネタになったのは言うまでもありません。
話が大幅にそれましたが、カレー屋での出来事に戻ります。ここからがパラドックスの本文です(実際の出来事とは関係ありません)。
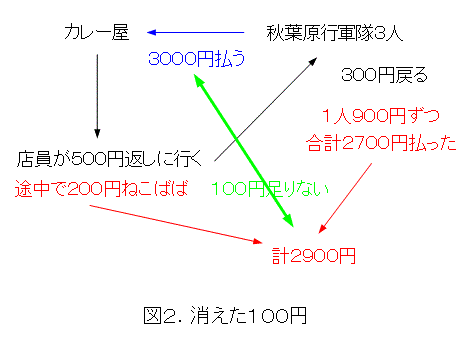
3人がカレー屋でカレーを食い、それぞれ1000円ずつ払い、店を出ました。すると、店のおやじが、「今日はカレーの日だから、3人で2500円でいい。500円返して来い。」と店員に言いました。店員は、3人を追いかけ、返しに行きましたが、その途中で、「3人じゃ500円を割り切れない。どうせ値引きになったことは知らないんだし、200円ねこばばして返したって喜ぶだろ。」と思い、その通りに実行しました。当然3人は喜んで、店員にお礼をいいました。
さて、店員がよく考えたところ、3人はそれぞれ900円ずつ払ったことになりますので、合計2700円払ったことになります。店員が200円ねこばばしたので、それを足すと2900円ですね。最初、店には3000円払っていたので、100円足りません。どこへ行ったのでしょう。
4.核攻撃は必ず受ける
核兵器が存在する以上、どの場所も核攻撃を受ける確率が0ではありません。確率がどんな値でも話は同じなので、以下のように考えましょう。どの場所も核攻撃を受けるか、受けないかのどっちかしかないので、ここは折半して受ける確率も、受けない確率も1/2とします(他の値にしても同じです)。
すると、この町が核攻撃を受けない確率は1/2です。この町とあの町が核攻撃を受けない確率は、この町が受けなくて、あの町も受けないということですから、1/2と1/2の積になります。次に、この町とあの町とその町が受けない確率は1/2と1/2と1/2の積になります。以下同様に考えて、全ての町が核攻撃を受けない確率は、1/2を町の数だけ掛けた値になります。
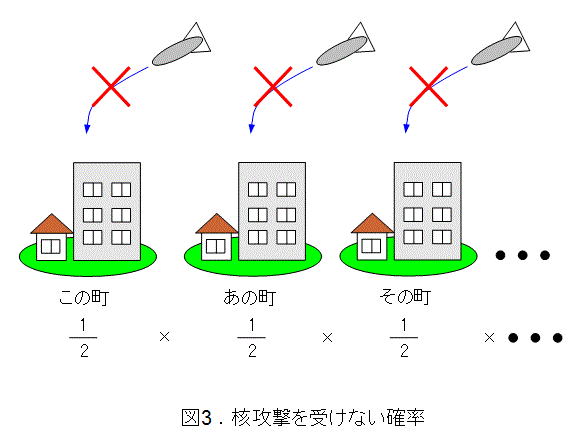
したがって、全ての町が核攻撃を受けない確率は相当0に近い値になります。これでも不満なら、この家が核攻撃を受けない確率、あの家が核攻撃を受けない確率、その家が核攻撃を受けない確率などとしましょう。もっと0に近づけたいときは、俺が核攻撃を受けない確率、あいつが核攻撃を受けない確率、そいつが核攻撃を受けない確率などとすればよいでしょう。
相当小さな値なので、どこも核攻撃を受けない確率は0と見なしてよくなります。
核攻撃を受けるという事象は、どこも核攻撃を受けないという事象の反対です。
これから、
核攻撃を受ける確率=1−どこも核攻撃を受けない確率=1
となりますね。
つまり、核攻撃は必ず受けるという結論に達します。
ちゃんと解決したい人は確率論の勉強をしましょう。
5.数値は何でも同じ
最後は、与えられた円で、勝手に弦を引くとき、その弦の長さが、内接する正三角形の一辺より長くなる確率を求めましょう。ここで、円の中心をO、内接する正三角形の頂点をA、B、C、ADを円の直径としておきます。
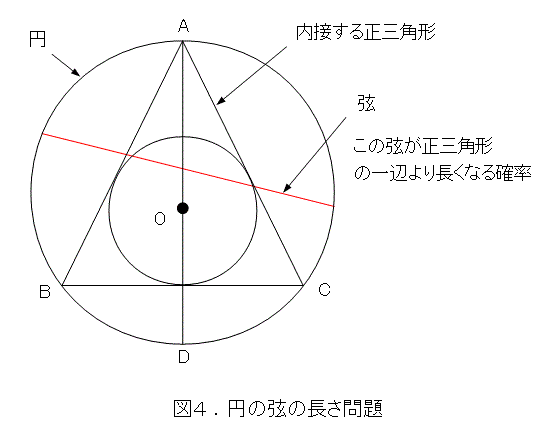
さて、勝手に引いた弦が、正三角形の一辺より大きくなるのは、弦の中点が正三角形の内接円内にあることが必要十分条件です。
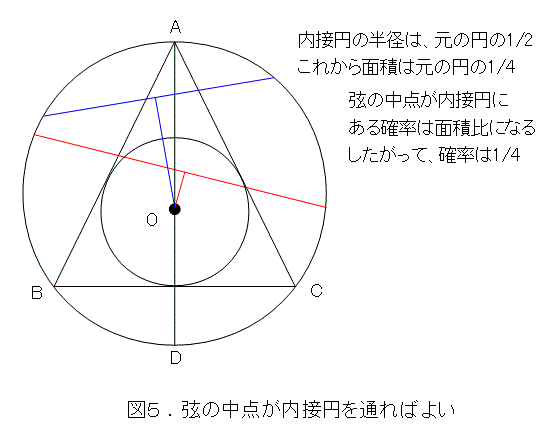
図5から、求める確率は1/4となりました。
いや、ちょっと待てよ。弦をOのまわりに適当に回転して、ADに垂直な位置にもってくることができます。そうすると、最初から、ADに垂直な弦だけを考えても一般性は失われません。
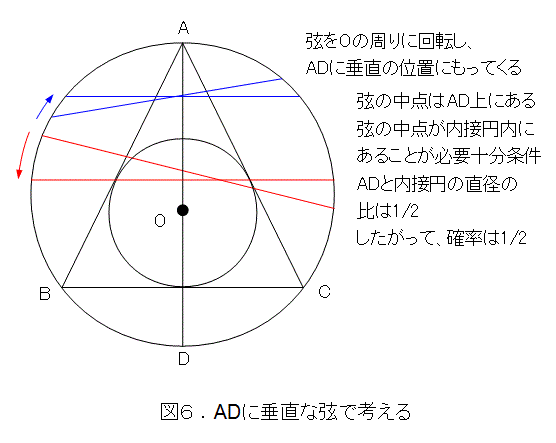
今度は、図6から、求める確率は1/2となりました。
ちょっと待ったに待った。なんかへぼ将棋みたいになってきましたね。 弦を Oのまわりに回転する際に、弦の一端がAと重なるようにできます。そうすると、点Aを通る弦だけを考えても一般性は失われません。
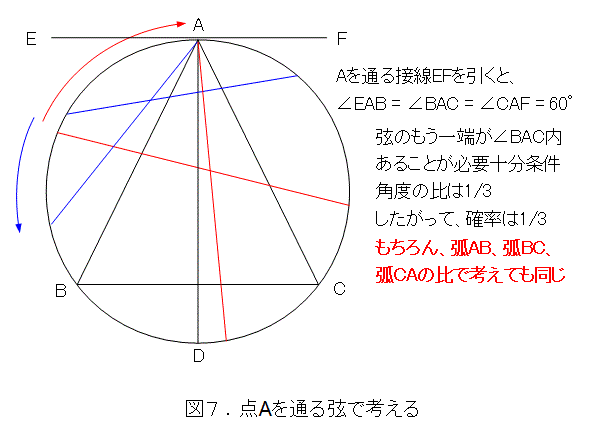
図7から、求める確率は1/3となりました。
なんと、答えが3つも出てしまいました。この際だから、更に惑わせることを書きましょう。図7の赤字で書いた部分に注目します。
点Aで円Oに接する曲線を引き(どっかがぶっとんで無限に長くてもよい)、図8のようにします。

すると、図8で引いた曲線は、どんな曲線にしても同じですので、求める確率は、0から1までのどんな値にすることもできます。
ちゃんと解決したい人は確率論の勉強をしましょう。では足りなくて、「科学全般を勉強しましょう。」ということになりましょうか。これでは不親切なので、ちょっとだけ説明をします。
そもそも、どこかに真理があって、それを追求しているのが科学ではありません。何を仮定すれば何が結論されるかという、論理の連鎖(の積み重ね)が科学です。今回の場合、仮定が何も書かれていません(確率分布が不明)。つまり、出発点が全くもって不明な訳です。なんだか解らないところから、勝手な仮定をして結論を導き出しています。そういう目で本章を読み直すことをお勧めします。
6.おわりに
何でも数値で表せばいいという風潮があります。しかし、うっかり数値を信用するのは危険です。前回の初等幾何のパラドックスと違い、作図すればなんとかなる問題ではありません。仮定から推論過程までの検証と、多くの知識を必要とします。
また、人によって数値の意味が違っていたり、価値が違う場合もよくあります。同じ1万円でも、大金だと思う人(俺)もいれば、大した額じゃないと思う人もいます。これもまたやっかいです。
このように、数値にはいたるところに罠が仕掛けられています。したがって、都合のいいデータを使い、都合のいい結論を出すには都合がいいですね。前回の「おわりに」で書いた手口がそうです。実感と、どっかの国の政府が言ってることが合わないのは、まさにこのためです。
色々とねつ造の手口はありますが、それを見破る目を持ちたいものです。それには、やはり、思考訓練を多く積む以外にないでしょう。
完
平成26年10月9日
著作者 坂田 明治(あきはる)
|